In ΔABC,∠A=x+15∘,∠B=xand∠C=2x−35∘ find, each angle of the triangle.
The correct Answer is:65∘,50∘and65∘
To find the angles of triangle ABC where angle A = x + 15°, angle B = x°, and angle C = 2x - 35°, we can follow these steps:
1. Use the Angle Sum Property of a Triangle:
The sum of the angles in a triangle is always 180°. Therefore, we can write the equation:
Angle A+Angle B+Angle C=180°
Substituting the expressions for the angles, we have:
(x+15)+x+(2x−35)=180
2. Combine Like Terms:
Simplifying the left side of the equation:
x+15+x+2x−35=180
This simplifies to:
4x−20=180
3. Isolate x:
To solve for x, first add 20 to both sides:
4x=180+20
4x=200
Now, divide both sides by 4:
x=2004=50
4. Calculate Each Angle:
Now that we have the value of x, we can find each angle:
- Angle A:
Angle A=x+15=50+15=65°
- Angle B:
Angle B=x=50°
- Angle C:
Angle C=2x−35=2(50)−35=100−35=65°
5. Final Angles:
Therefore, the angles of triangle ABC are:
- Angle A = 65°
- Angle B = 50°
- Angle C = 65°
Summary:
- Angle A = 65°
- Angle B = 50°
- Angle C = 65°
The sum of the angles in a triangle is always 180°. Therefore, we can write the equation:
Angle A+Angle B+Angle C=180°
Substituting the expressions for the angles, we have:
(x+15)+x+(2x−35)=180
Simplifying the left side of the equation:
x+15+x+2x−35=180
This simplifies to:
4x−20=180
To solve for x, first add 20 to both sides:
4x=180+20
4x=200
Now, divide both sides by 4:
x=2004=50
Now that we have the value of x, we can find each angle:
- Angle A:
Angle A=x+15=50+15=65°
- Angle B:
Angle B=x=50°
- Angle C:
Angle C=2x−35=2(50)−35=100−35=65°
Therefore, the angles of triangle ABC are:
- Angle A = 65°
- Angle B = 50°
- Angle C = 65°
- Angle A = 65°
- Angle B = 50°
- Angle C = 65°
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Revision Exercise (very Short Answer Questions )10videos
LINES AND ANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Revision Exercise (short Answer Questions)12videos
LINES AND ANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6 B16videos
LINES AND ANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Revision Exercise12videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - NUMBER SYSTEMEXERCISE - Revision Exercise (short Answer Questions)10videos
NUMBER SYSTEM
Similar Questions
In ΔABC,∠A−∠B=16∘and∠C−∠A=34∘=34∘ , find all angles of the triangle
View SolutionIn a ΔABC, if ∠A=45∘.∠B=60∘and∠C=75∘, find the ratio of its sides.
View SolutionIn ΔABC,∠A=600,∠B=45∘, find a:b.
View SolutionIn a ΔABC,∠A=2∠B=3∠C, find each of the triangle.
View SolutionThe following figure shows a quadrilateral in which sideo AB and DC are parallel. If ∠A:∠D=4:5,∠B=(3x−15)∘and∠C=(4x+20)∘, find each angle of the quadrilateral ABCD.
 View Solution
View SolutionIn ΔABC,∠A=2πc3 and ∠B=45∘. Find ∠C in both the systems.
View SolutionIn the given figure ∠A=x+8∘,∠B=2x+3∘and∠BCD=5x−11∘, find the measure of ∠BCD
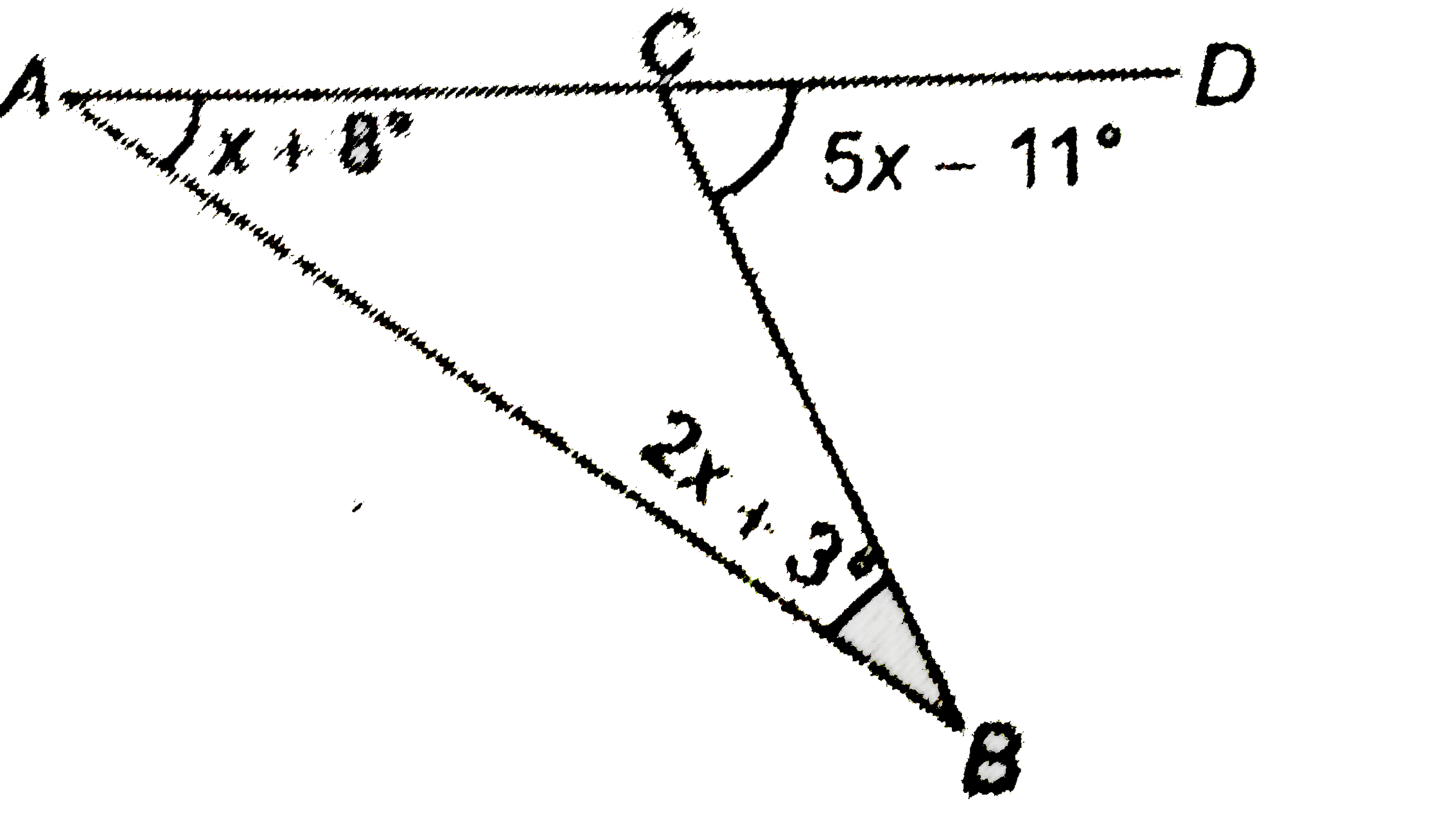 View Solution
View SolutionΔABC , ∠A+∠B=65∘, ∠B+∠C=140∘,then ∠B is equal to
View SolutionIn ΔABC,∠B=90∘,∠A=30∘,b=20cm, find a and c.
View SolutionEach base angle of an isosceles triangle is 15∘ more than its vertical angle. Find each angle of the triangle.
View Solution
