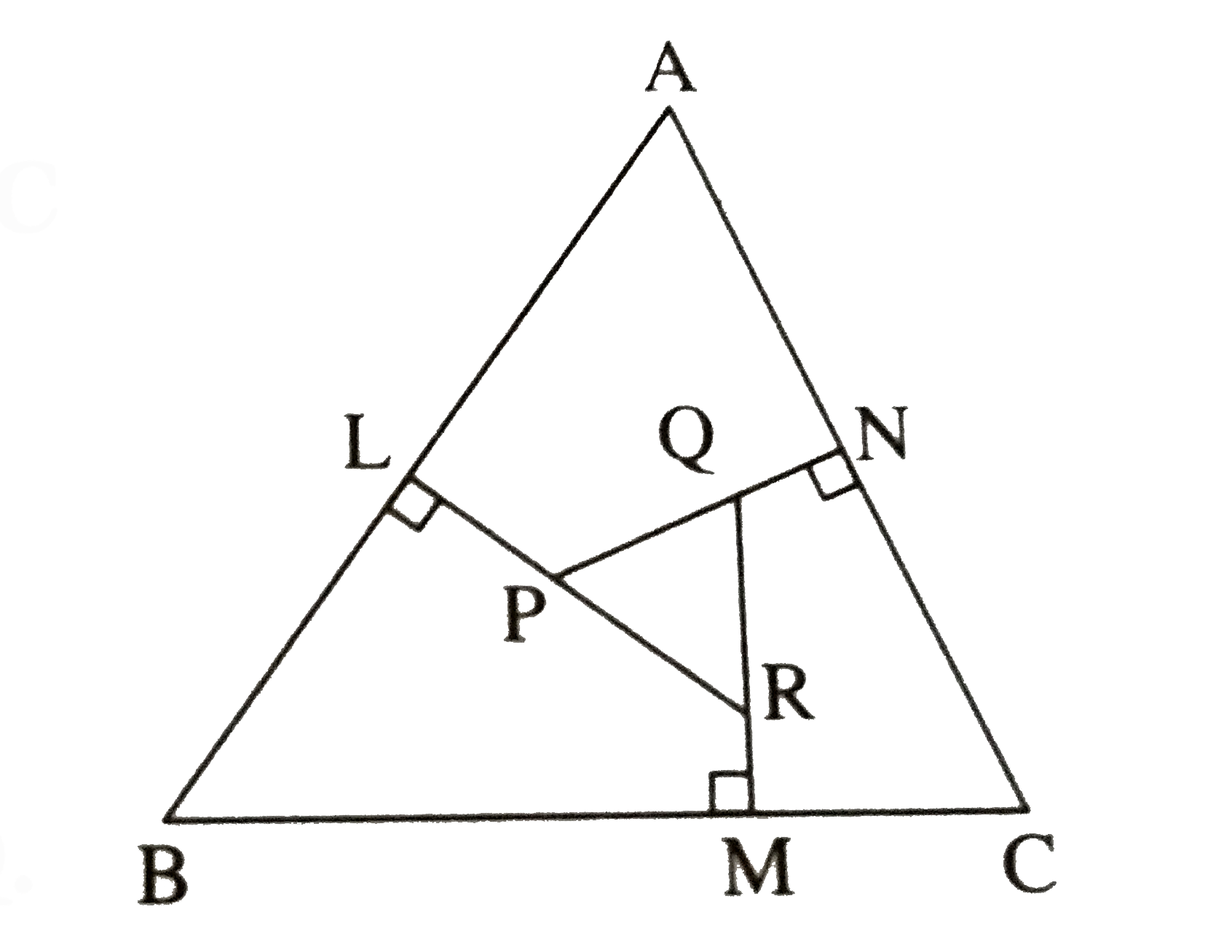
In ΔABC,L,M,Nare points on side AB,BC,AC respectively.
Perpendiculars drawn at L,M,N form ΔPQR.
Prove that ΔABC~ΔPRQ.
NA
Topper's Solved these Questions
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - MCQ TYPE
15 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - SUBJECTIVE TYPE
20 Videos
- SIMILARITYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - EXAMPLE TYPE
50 Videos
- QUADRATIC EQUATIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.4
8 Videos
- STATISTICSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)
35 Videos
Similar Questions
In ΔABC , if L and M are the points on AB and AC, respectively such that LM∣∣BC. Prove that ar(ΔLOB)=ar(ΔMOC).
View SolutionIn the given figure, the two sides AB and BC, and the median AD of ΔABC are correspondingly equal to the two sides PQ and QR, and the medium PM of ΔPQR. Prove that ΔABC≅ΔPQR.
View Solution
Knowledge Check
In ΔABC, two points D and E are taken on the lines AB and BC respectively in such a way that AC is parallel to DE. Then ΔABCandΔDBEare
Asimilar only if D lies outside the line segment ABBcongruent only if D lies out side the line segment ABCalways similarDalways congruentIn a ΔABC,DandEare points on AC and BC respectively, AB and DE are perpendicular to BC. If AB=9cm,DE=3cmandAC=24cm, then AD is :
A32cmB16cmC8 cmD4 cm
The sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionIn ΔABC PQ||BC. P and Q lies on side AB and AC respectively. If AB = 3AP, then what is the ratio of areas of ΔAPQandΔABC?
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2AD
View SolutionIn the given Fig. 3, in ΔABC,DandE are the mid point of the sides AB and AC respectively. Find the length of DE. Prove that DE=12BC.
View SolutionK, L, M and N are points on the sides AB, BC, CD and DA respectively of a square ABCD such that AK = BL = CM = DN. Prove that KLMN is a square.
View SolutionIf H be orthocentre of ΔABC and mid point of AH, BH, CH are respectively P, Q, R then prove that H is also the orthocentre of ΔPQR and ΔPQR−ΔABC.
View Solution
