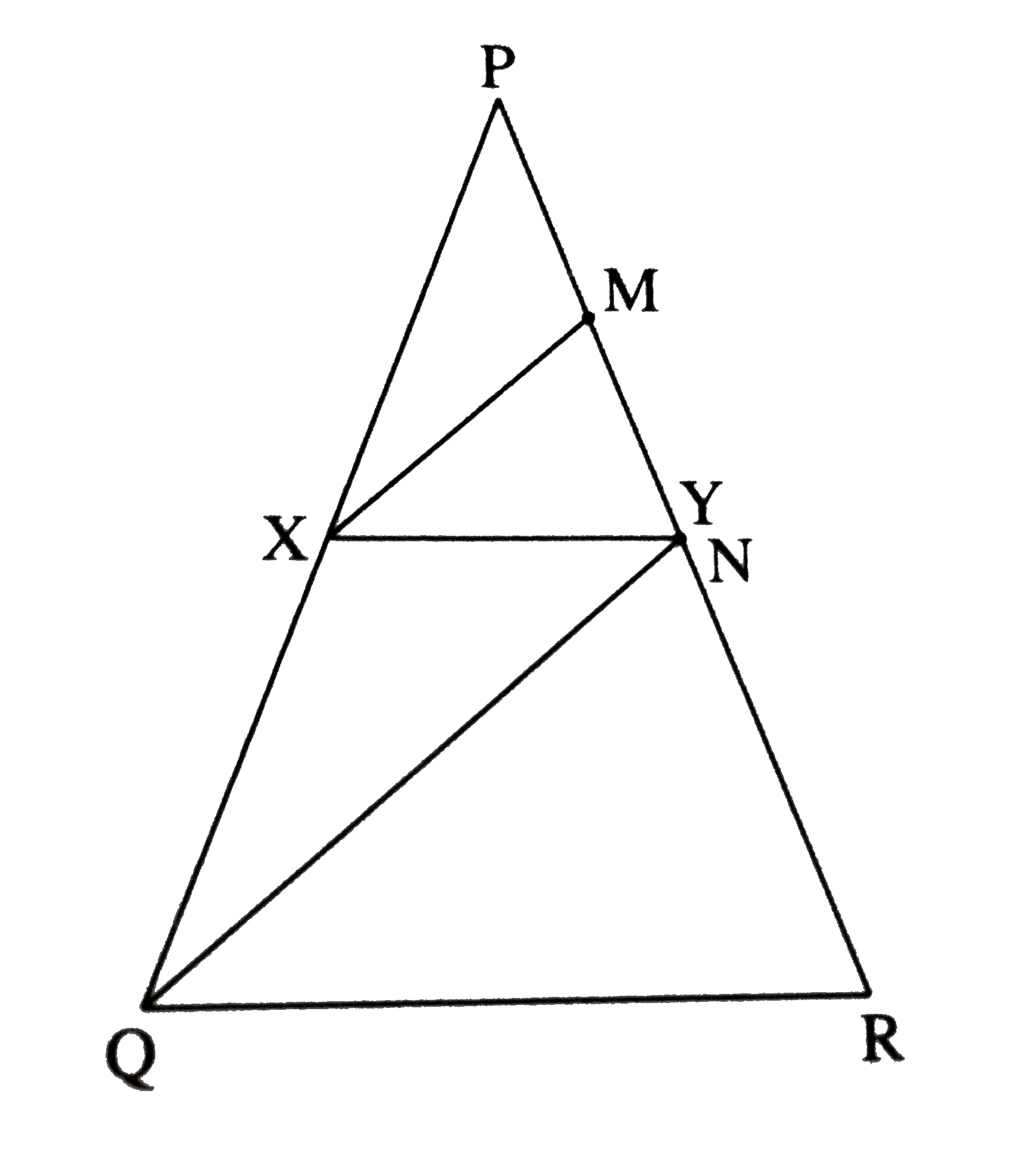
In ΔPQR, seg XY∣∣ side QR. M and N are the midpoints of seg PY and side PR respectively, P−M−Y−N−R.
Prove that (i)ΔPXM~ΔPQN
(ii) seg XM∣∣ seg QN.
Video Solution
Text Solution
In ΔPXY and ΔPQR,
∠PXY≅∠PQR……(Seg XY∣∣ side QR, corresponding angles)
∠XPY≅∠QPR…..(Common angle)
∴ΔPXY~ΔPQR……("AA"test for similarity)
∴PXPQ=PYPR………..(c.s.s.t)…….(1)
Point M and N are the midpoints of seg PY seg PR respectively. .......(Given)
∴PY=2PM and PR=2PN........(2)
∴PXPQ=2PM2PN.....[From (1) and (2)]
∴PXPQ=PMPN ........(3)
In ΔPXM and ΔPQN,
PXPQ=PMPN [From (3)]
∠XPM≅∠QPN.......(Common angle)
∴ΔPXM~ΔPQN ......(SAS test for similarity)
∴∠PXM=∠PQN........(c.a.s.t)
∴ seg XM∣∣ seg QN.........(Corresponding angles test for parallel lines)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - EXAMPLE TYPE50videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - CHALLENGING QUESTIONS8videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SIMILARITYEXERCISE - 2.4 (3 mark each)8videos
SIMILARITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNEMENT 2.48videos
QUADRATIC EQUATIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - STATISTICSEXERCISE - EXAMPLES FOR PRACTICE (MCQs)35videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Let □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NM - Question 2 - Select One
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3 - Question 3 - Select One
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3
In ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
 View Solution
View Solution
In the figure, M and N are the midpoints of sides PQ and PR respectively . If MN =6 cm then find QR. State your reason .View SolutionM and N are the points on sides QR and PQ respectively of a △PQR, right angled at Q. prove that PM2+RN2=PR2+MN2
View SolutionIn ΔABC,L,M,Nare points on side AB,BC,AC respectively.
Perpendiculars drawn at L,M,N form ΔPQR.
Prove that ΔABC~ΔPRQ.
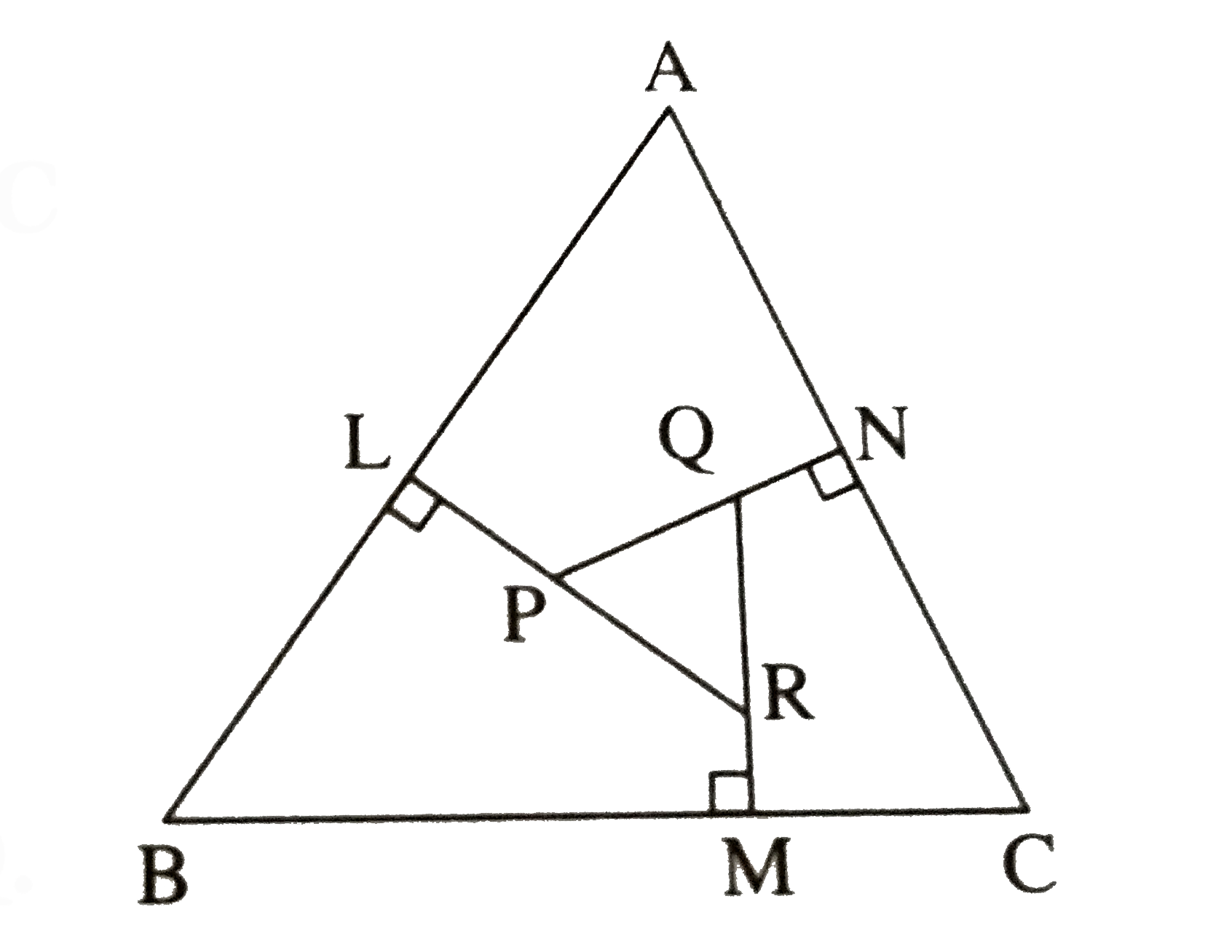 View Solution
View SolutionLet D(x4,y4) be a point such that ABCD is a square and M and P are the midpoints of the sides BC&CD respectively, then
View Solution