Question

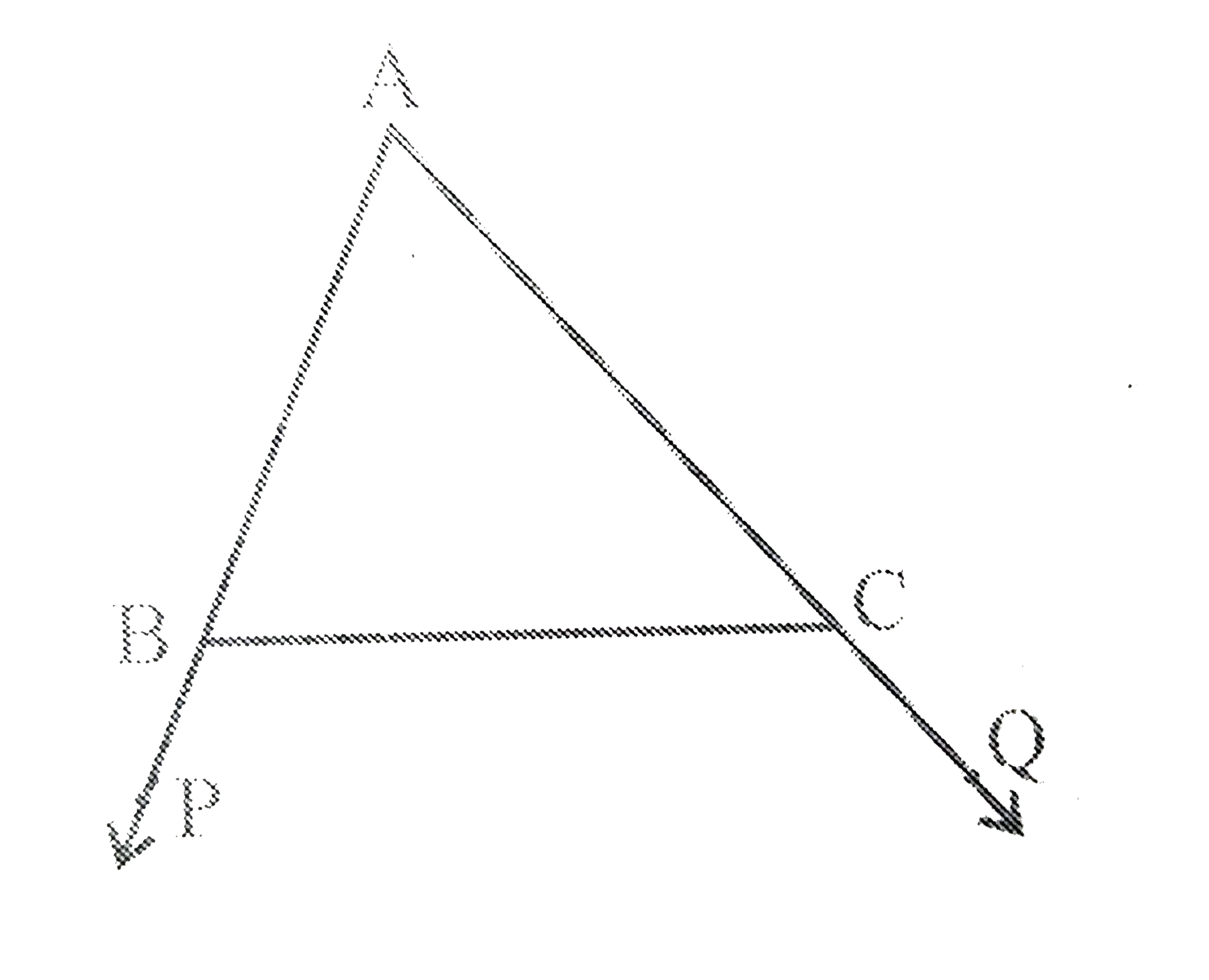
In Fig.
10.20, the sides $AB,BC$
and $CA$
of triangle
$ABC$
touch a
circle with centre $O$
and radius $r$
at $P,Q$
and $R$
respectively.
(FIGURE)


Prove that:
1) AB + CQ = AC + BQ

Explanation

To prove that $$AB+CQ=AC+BQ$$, we will use the properties of tangents drawn from a point outside a circle.

1. Identify Tangents from Points:
From point \( A \) to the circle, the tangents are \( AP \) and \( AR \). By the property of tangents from a point outside a circle, we know that:
\( AP = AR \)

2. Identify Tangents from Point B:
From point \( B \) to the circle, the tangents are \( BQ \) and \( BP \). Again, by the property of tangents:
\( BQ = BP \)

3. Identify Tangents from Point C:
From point \( C \) to the circle, the tangents are \( CQ \) and \( CR \). Thus, we have:
\( CQ = CR \)

4. Add the Tangent Lengths:
Now, we can add the lengths of the tangents from points \( A \), \( B \), and \( C \):
\( AP + BP + CQ = AR + CR + BQ \)

5. Substituting the Tangent Lengths:
We know that \( AP + BP = AB \) and \( AR + CR = AC \). Thus, we can rewrite the equation:
\( AB + CQ = AC + BQ \)

6. Conclusion:
Therefore, we have proved that:
\( AB + CQ = AC + BQ \)