In Fig. 10.74, and are tangents to a circle with centre . is another tangent touching the circle at . If and , then find the length of . (FIGURE)
To solve the problem step by step, we will use the properties of tangents to a circle.
1. Identify the Given Information:
- Length of tangent CP=11cm
- Length of segment BC=7cm
2. Use the Property of Tangents:
- Since CP and CQ are tangents from point C to the circle, we know that CP=CQ.
- Therefore, CQ=11cm.
3. Establish Relationships:
- From point B, there are two tangents to the circle: BR and BQ.
- By the property of tangents from a point outside the circle, we have BR=BQ.
4. Express CQ in terms of BC and BQ:
- We can express CQ as:
CQ=BC+BQ
- Substituting the known values:
11cm=7cm+BQ
5. Solve for BQ:
- Rearranging the equation gives:
BQ=11cm−7cm=4cm
6. Find BR:
- Since BR=BQ, we have:
BR=4cm
Final Answer:
The length of BR is 4cm.
---
- Length of tangent CP=11cm
- Length of segment BC=7cm
- Since CP and CQ are tangents from point C to the circle, we know that CP=CQ.
- Therefore, CQ=11cm.
- From point B, there are two tangents to the circle: BR and BQ.
- By the property of tangents from a point outside the circle, we have BR=BQ.
- We can express CQ as:
CQ=BC+BQ
- Substituting the known values:
11cm=7cm+BQ
- Rearranging the equation gives:
BQ=11cm−7cm=4cm
- Since BR=BQ, we have:
BR=4cm
The length of BR is 4cm.
Topper's Solved these Questions
Similar Questions
In Fig. 10.74, CP and CQ are tangents to a circle with centre O . ARB is another tangent touching the circle at R . If CP=11cm and BC=7cm , then find the length of BR . (FIGURE)
View SolutionCP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm, BC = 7cm, Then the length BR is :
View Solution
Knowledge Check
In the figure , CP and CQ are tangent to a circle with centre O.ARB is another tangent touching the circle R . If CP =11 and BC = 7 cm then what is the length of BR?
(##CEN_JEE_MAT_X_C14_E01_043_Q01.png" width="80%">A2 cmB4 cmC6 cmD8 cmIn the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
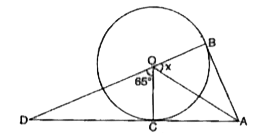 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘
In figure, CP and CQ are tangents from an external point C to a circle with centre O. AB is another tangent which touches the circle at R. If CP = 11 cm and BR = 4 cm. Find the length of BC.
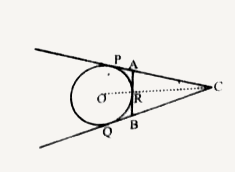
View SolutionIn Fig. 10.76, CP and CQ are tangents from an external point C to a circle with centre O . AB is another tangent which touches the circle at R . If CP=11cm and BR=4cm , find the length of BC . (FIGURE)
View SolutionIn Fig. 15.92, two circles with centres A and B touch each other at the point C . If AC=8 cm and AB=3 cm , find the area of the shaded region. (FIGURE)
View SolutionXYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90o
View SolutionIn Fig. 10.79, RQ is a tangent to the circle with centre O . If SQ=6cm and QR=4cm , then OR= (FIGURE) (a) 8cm (b) 3cm (c) 2.5cm (d) 5cm
View Solutionlandm are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that∠DOE=90∘.
View Solution
