In Fig. 6.10, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ , respectively. If ∠POS=x , find ∠ROT .
To solve the problem step by step, we will analyze the given information and apply the properties of angles and their bisectors.
1. Identify the Given Angles:
- We know that ∠POS=x.
- Ray OR is the angle bisector of ∠POS.
- Ray OT is the angle bisector of ∠SOQ.
2. Determine the Angles Created by the Bisectors:
- Since OR bisects ∠POS, we can express the angles as:
∠POR=∠SOR=x2
3. Express the Angle ∠SOQ:
- Since OS is a straight line, the sum of angles ∠POS and ∠SOQ must equal 180∘:
∠POS+∠SOQ=180∘
- Substituting ∠POS=x:
x+∠SOQ=180∘
- Therefore, we can find ∠SOQ:
∠SOQ=180∘−x
4. Determine the Angles Created by the Bisector OT:
- Since OT bisects ∠SOQ, we can express the angles as:
∠SOT=∠TOQ=180∘−x2
5. Calculate ∠ROT:
- The angle ∠ROT can be expressed as the sum of ∠ROS and ∠SOT:
∠ROT=∠ROS+∠SOT
- We already found that ∠ROS=x2 and ∠SOT=180∘−x2:
∠ROT=x2+180∘−x2
6. Combine the Angles:
- Combine the fractions:
∠ROT=x+180∘−x2=180∘2=90∘
Final Answer:
Thus, we find that:
∠ROT=90∘
- We know that ∠POS=x.
- Ray OR is the angle bisector of ∠POS.
- Ray OT is the angle bisector of ∠SOQ.
- Since OR bisects ∠POS, we can express the angles as:
∠POR=∠SOR=x2
- Since OS is a straight line, the sum of angles ∠POS and ∠SOQ must equal 180∘:
∠POS+∠SOQ=180∘
- Substituting ∠POS=x:
x+∠SOQ=180∘
- Therefore, we can find ∠SOQ:
∠SOQ=180∘−x
- Since OT bisects ∠SOQ, we can express the angles as:
∠SOT=∠TOQ=180∘−x2
- The angle ∠ROT can be expressed as the sum of ∠ROS and ∠SOT:
∠ROT=∠ROS+∠SOT
- We already found that ∠ROS=x2 and ∠SOT=180∘−x2:
∠ROT=x2+180∘−x2
- Combine the fractions:
∠ROT=x+180∘−x2=180∘2=90∘
Thus, we find that:
∠ROT=90∘
Topper's Solved these Questions
Similar Questions
In Figure, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ respectively. If ∠POS=x, find ∠ROT
View SolutionIn Figure, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ respectively. If ∠POS=x, find ∠ROT
View SolutionIn Figure, PQ>PR.QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ>SR.
View SolutionIn Fig.29, POS is a line, find x.
View SolutionIn Figure, O is the centre of a circle and PQ is a diameter. If ∠ROS=400, find ∠RTS
View SolutionIn Figure, POS is a line, find x
View SolutionIn Fig.9, if ray OC stands on line AB such that ∠AOC=∠COB, then show that ∠AOC=900.
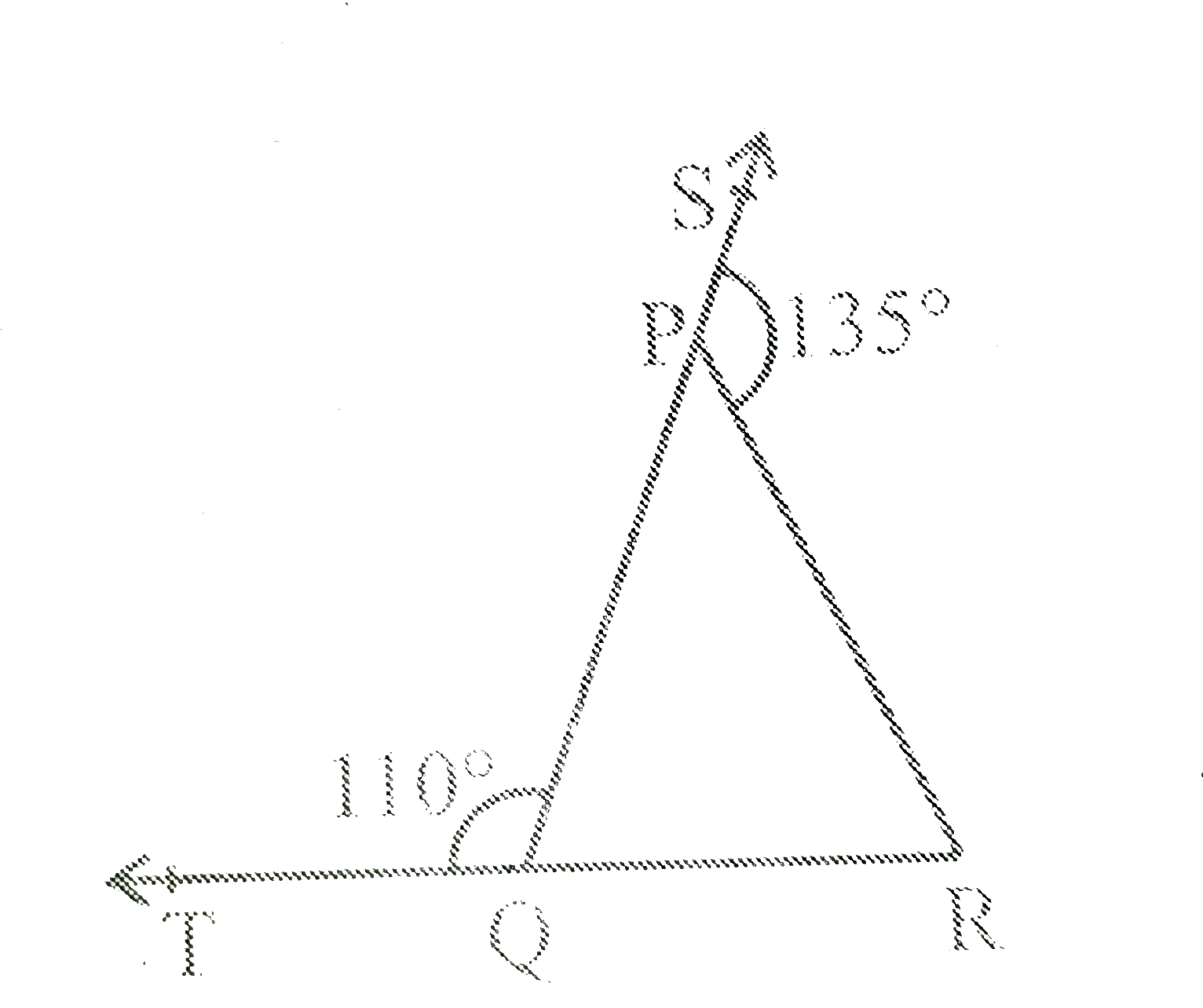
View Solutionsides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ.
View SolutionIf ray OC stands on line AB such that ∠AOC=∠COB , then show that ∠AOC=900
View SolutionIn Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
 View Solution
View Solution

