In Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
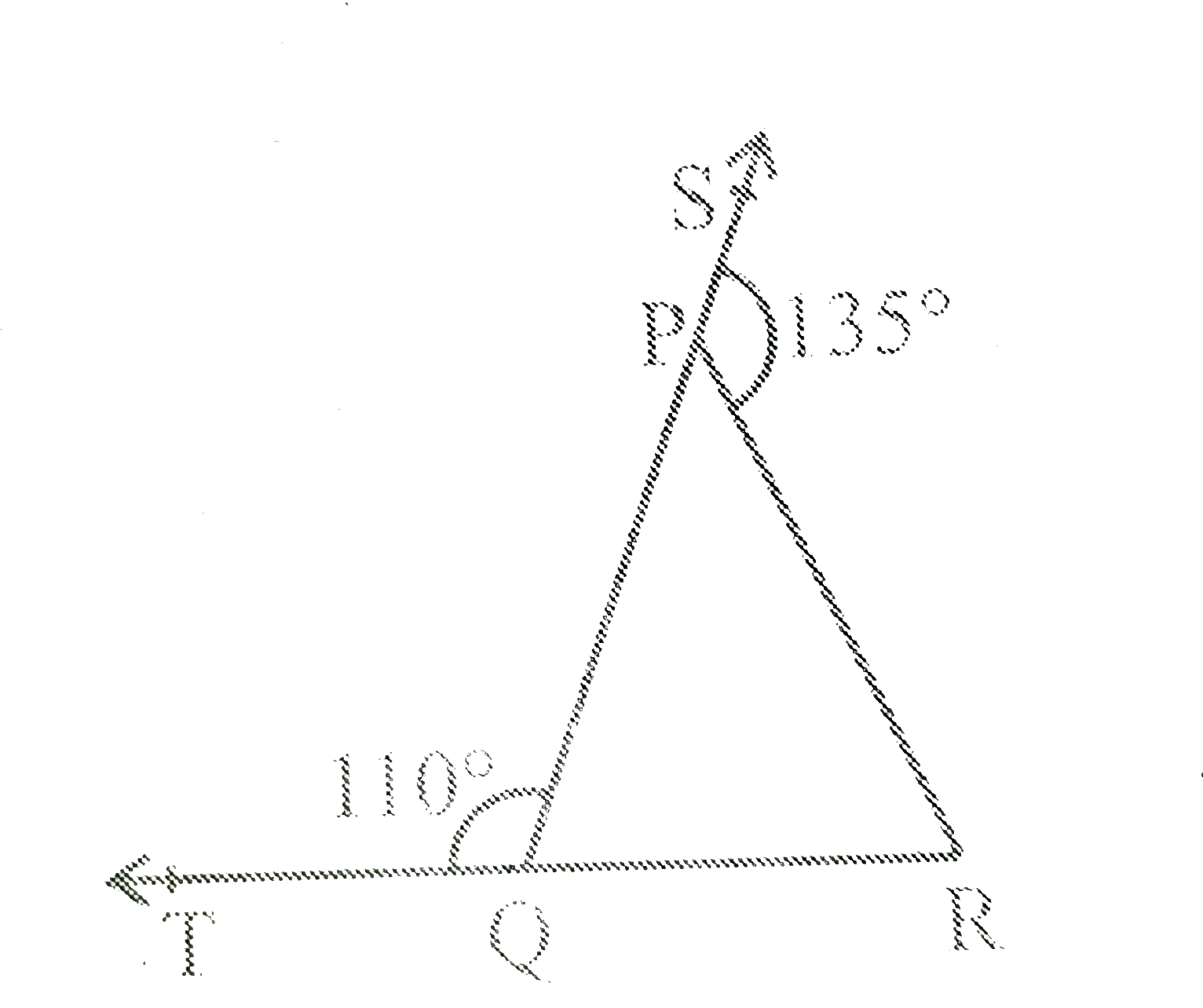
∠PQT+∠PQR=180∘
(Straight angle made on line TR at point Q)
110∘+∠PQR=180∘
∠PQR=180∘−110∘=70∘
In △PQR
∠PSR=∠PQR+∠PRQ (Exterior angle of triangle is eqal to sum of two interior angles)
135∘=70∘+∠PRQ⇒<br>∠PRQ=135∘−70∘=65∘
Similar Questions
sides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ.
View SolutionIn figure, sides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ. Figure
View SolutionIn figure, sides QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350 and ∠PQT=1100, find ∠PRQ. Figure
View SolutionIn Figure, side QP and RQ of PQR are produced to point S and T respectively. If ∠SPR=1350and ∠PQT=110∘, find ∠PRQ
View SolutionIn Figure, TQ and TR are the bisectors of ∠Q and ∠R respectively. If ∠QPR=800and ∠PRT=300, determine ∠TQR and ∠QTR
View SolutionIn Fig. , the side QR of △ PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.
 View Solution
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR\ and∠PRS meet at point T, then prove that ∠QTR=12∠QPR .
View SolutionIn Fig. 6.10, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ , respectively. If ∠POS=x , find ∠ROT .
View SolutionIn Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.
 View Solution
View SolutionIn Figure , find out ∠PXR, if PQ ∣∣ RS.
 View Solution
View Solution

