Question

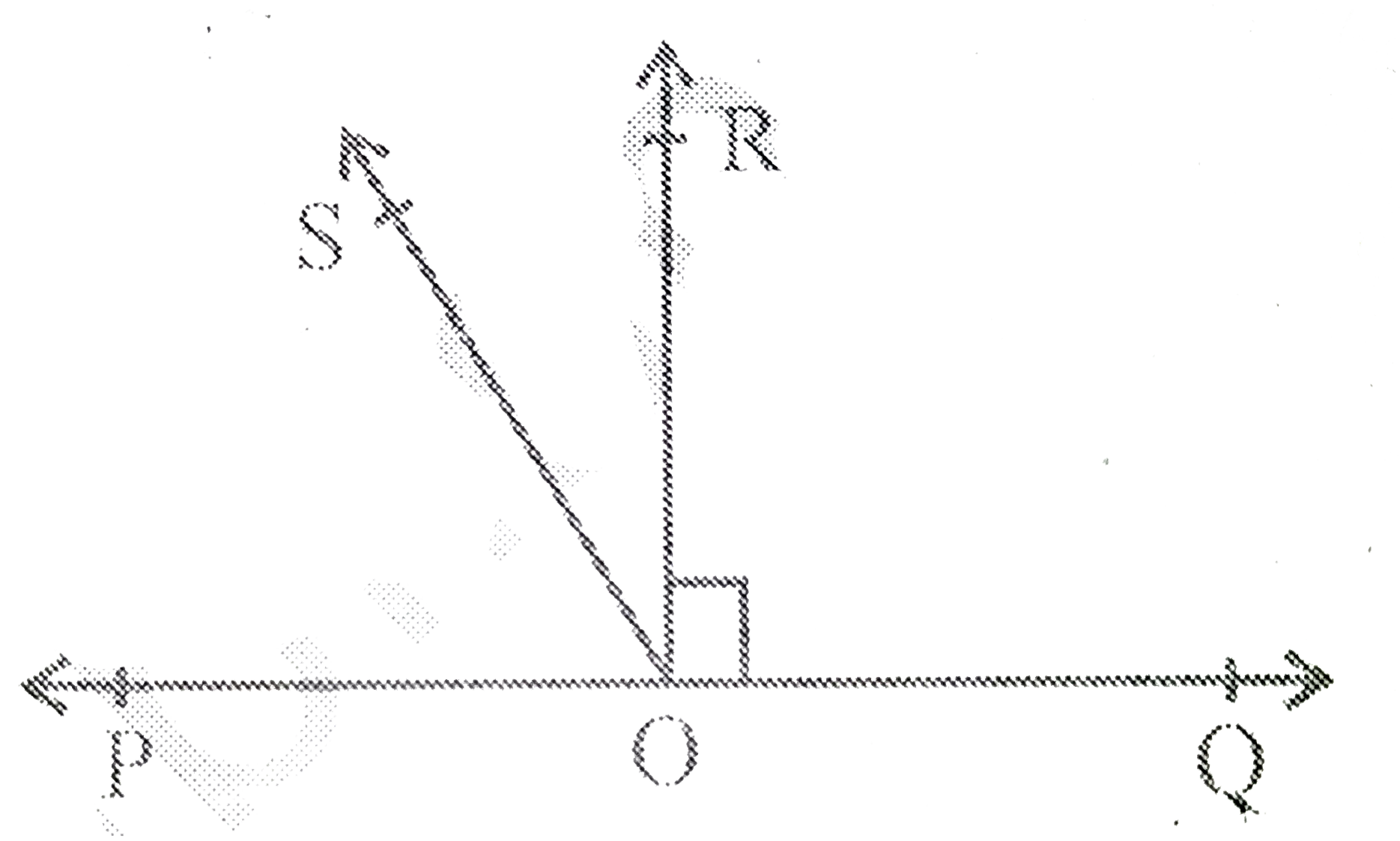
In Fig.29, $POS$
is a line, find $x\stackrel{.}{}$

Options

A. 20
B. 40
C. 80
D. 180

Answer

A

Explanation

To solve for $$x$$ in the given problem, we will follow these steps:

Step 1: Understand the problem
We have a straight line \( POS \) and three angles formed by points \( P, O, Q, R, S \). The angles are given as follows:
- \( \angle POQ = 60^\circ \)
- \( \angle ROS = 40^\circ \)
- \( \angle QOR = 4x \)

Since \( POS \) is a straight line, the sum of the angles around point \( O \) must equal \( 180^\circ \).

Step 2: Set up the equation
We can set up the equation based on the angles:
\( \angle POQ + \angle QOR + \angle ROS = 180^\circ \)
Substituting the values we know:
\( 60^\circ + 4x + 40^\circ = 180^\circ \)

Step 3: Simplify the equation
Combine the constant angles:
\( 100^\circ + 4x = 180^\circ \)

Step 4: Solve for \( 4x \)
Subtract \( 100^\circ \) from both sides:
\( 4x = 180^\circ - 100^\circ \)
\( 4x = 80^\circ \)

Step 5: Solve for \( x \)
Now, divide both sides by \( 4 \):
\( x = \frac{80^\circ}{4} \)
\( x = 20^\circ \)

Final Answer
Thus, the value of \( x \) is \( 20^\circ \).

---