Question

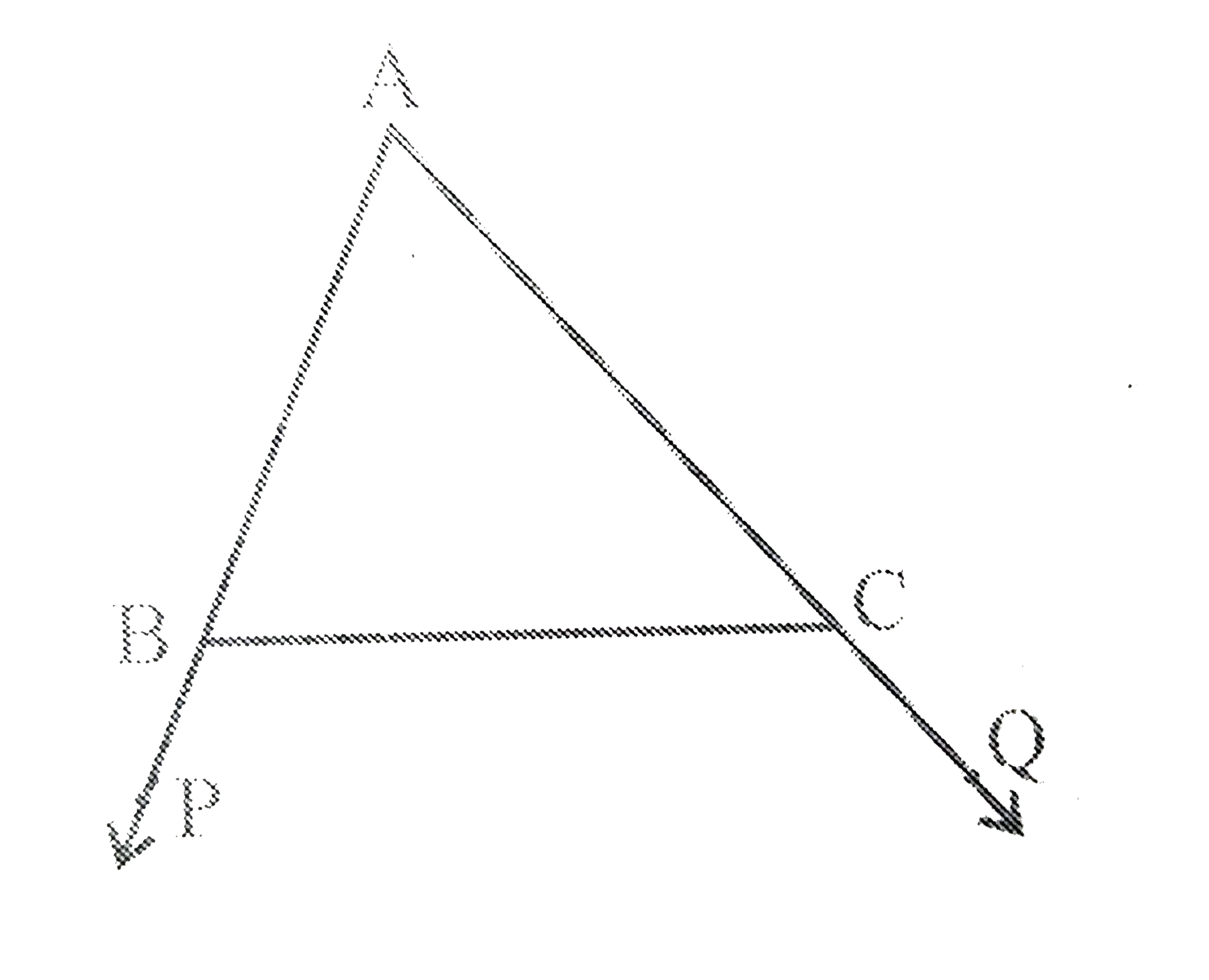
In Fig. 6.38, the sides AB and AC of ABC are produced to points E and D respectively. If bisectors BO and CO of CBE and BCD respectively meet at point O, then prove that $\angle BOC={90}^{\circ }-\frac{1}{2}\angle BAC$.

Explanation

`∠CBE = 180 - ∠ABC`


`∠CBO = 1/2 ∠CBE` (BO is the bisector of ∠CBE)


`∠CBO = 1/2 ( 180 - ∠ABC) `
` 1/2 x 180 = 90 `

`∠CBO = 90 - 1/2 ∠ABC` .............(1)
` 1/2 x ∠ABC = 1/2∠ABC`




`∠BCD = 180 - ∠ACD`


`∠BCO = 1/2 ∠BCD ` ( CO is the bisector Is ∠BCD)


`∠BCO = 1/2 (180 - ∠ACD)`


`∠BCO = 90 - 1/2∠ACD ` ............(2)




`∠BOC = 180 - (∠CBO + ∠BCO)`


`∠BOC = 180 - (90 - 1/2∠ABC + 90 - 1/2∠ACD)`


`∠BOC = 180 - 180 + 1/2∠ABC + 1/2∠ACD`


`∠BOC = 1/2 (∠ABC + ∠ACD)`


`∠BOC = 1/2 ( 180 - ∠BAC) (180 -∠BAC = ∠ABC + ∠ACD)`


`∠BOC = 90 - 1/2∠BAC`