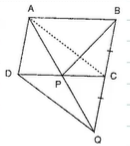
In Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) ar(APB)+ar(PCD)=12ar(ABCD)(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
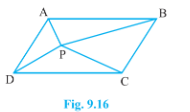
If a triangle and parallelogram are on the same base and between the same parallel lines, then the area of the triangle will be half of the area of the parallelogram.
i) Let us draw a line segment EF, passing through the point P and parallel to line segment AB in parallelogram ABCD
.AB∣∣EF (By construction) .....(1)
We know that ABCD is a parallelogram.
∴ AD∣∣BC (Opposite sides of a parallelogram are parallel)
AE∣∣BF ..... (2)
From Equations (1) and (2), we obtain
AB||EFandAE||BF
Therefore, quadrilateral ABFE is a parallelogram.
Similarly, it can be deduced that quadrilateral EFCD is a parallelogram.It can be observed that △APB and parallelogram ABFE is lying on the same base AB and between the same set of parallel lines AB and EF
Area(△APB) = 1/2 Area (ABFE) .....(3)
Similarly, for △PCD and parallelogram EFCD, Area (△PCD) = 1/2 Area (EFCD) .....(4)
Adding Equations (3) and (4), we obtain Area (△APB) + Area (△PCD) = 1/2 [Area (ABFE) + Area (EFCD)]
Area (△APB) + Area (△PCD) = 1/2 Area (ABCD) .....(5)
ii) Let us draw a line segment MN, passing through point P and parallel to line segment AD.
In parallelogram ABCD, MN∣∣AD (By construction) .....(6)
We know that ABCD is a parallelogram.
AB∣∣DC (Opposite sides of a parallelogram are parallel)
AM || DN.....(7)
From Equations (6) and (7), we obtainMN∣∣AD and AM∣∣DN
Therefore, quadrilateral AMND is a parallelogram.
It can be observed that △APD and parallelogram AMND is lying on the same base AD and between the same parallel lines AD and MN.
Area (△APD) = 1/2
Area (AMND) .....(8)
Similarly, for △PCB and parallelogramMNCB
Area (△PCB) = 1/2 Area (MNCB) .....(9)
Adding Equations (8) and (9), we obtain,
Area (△APD) + Area(△PCB) = 1/2 [Area (AMND) + Area (MNCB)]
Area (△APD) + Area (△PCB) = 12Area (ABCD) .....(10)
On comparing equations (5) and (10), we obtain
Area (△APD) + Area (△PBC) = Area (△APB) + Area(△PCD)
Similar Questions
In Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)
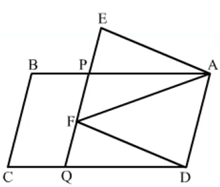
View SolutionIn Figure, ABCDandAEFD are two parallelograms? Prove that: ar(APE):ar(PFA)=ar(QFD):ar(PFD)
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View SolutionIf ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn ABC,D is the mid-point of AB,P is any point of BC.CQPD meets AB in Q . Show that ar(BPQ)=12ar(ABC). TO PROVE : ar(BPQ)=12ar(ABC) CONSTRUCTION : Join CD.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each at P. Show That: ar(APB)×ar(CPD)=ar(APD)×ar(PBC)
View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show thatar (APB) × ar (CPD) = ar (APD) × ar (BPC).
View Solution
