In fig . O is a point in the interior of a triangle ABC , OD ⊥BC,OE⊥ACandOF⊥AB . Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2+AE2+CD2+BF2 .
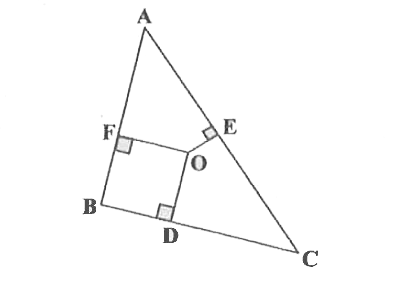
The correct Answer is:(i) OA2+OB2+OC2 , (ii) AF2+BD2+EC2+AE2+CD2+BF2
Topper's Solved these Questions
- TRIANGLESBOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Exercise 2.6 (Optional)
8 Videos
- TRIANGLESBOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Exercise 2.4
9 Videos
- SURFACE AREAS AND VOLUMES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - EXERCISE 15.4
5 Videos
Similar Questions
In the figure given below O is a point in the interior of a triangle ABC , OD ⊥ BC ,OE ⊥ AC and OF⊥AB . Show that

AF2+BD2+CE2=AE2+CD2+BF2
View SolutionO is a point in the interior of ΔABC,OD⊥BC,OE⊥ACandOF⊥AB, as shown in the figure,
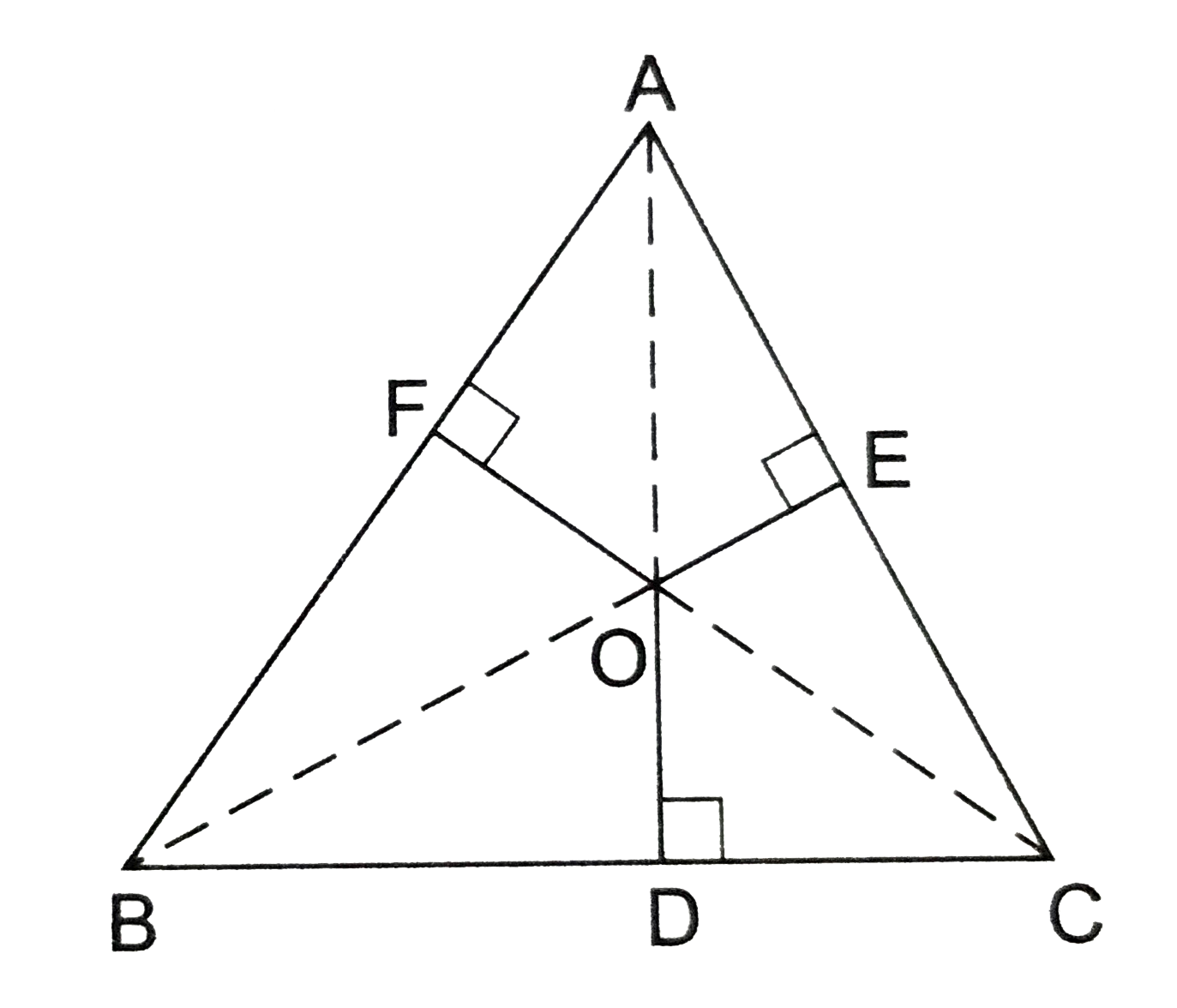
Prove that :
(i)OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AD2+BF2+CD2
View SolutionIn fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
View SolutionIn a ΔABC,∠B is an acute-angle and AD⊥BC
Prove that :
(i) AC2=AB2+BC2−2BC×BD
(ii) AB2+CD2=AC2+BD2
View SolutionFrom a point O in the interior of a ABC , perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: (i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2 (ii) AF2+BD2+CE2=AE2+CD2+BF2
View SolutionIn the figure , ABD is a triangle right angled at A and AC ⊥ Bd . Show that

AD2=BD⋅CD
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
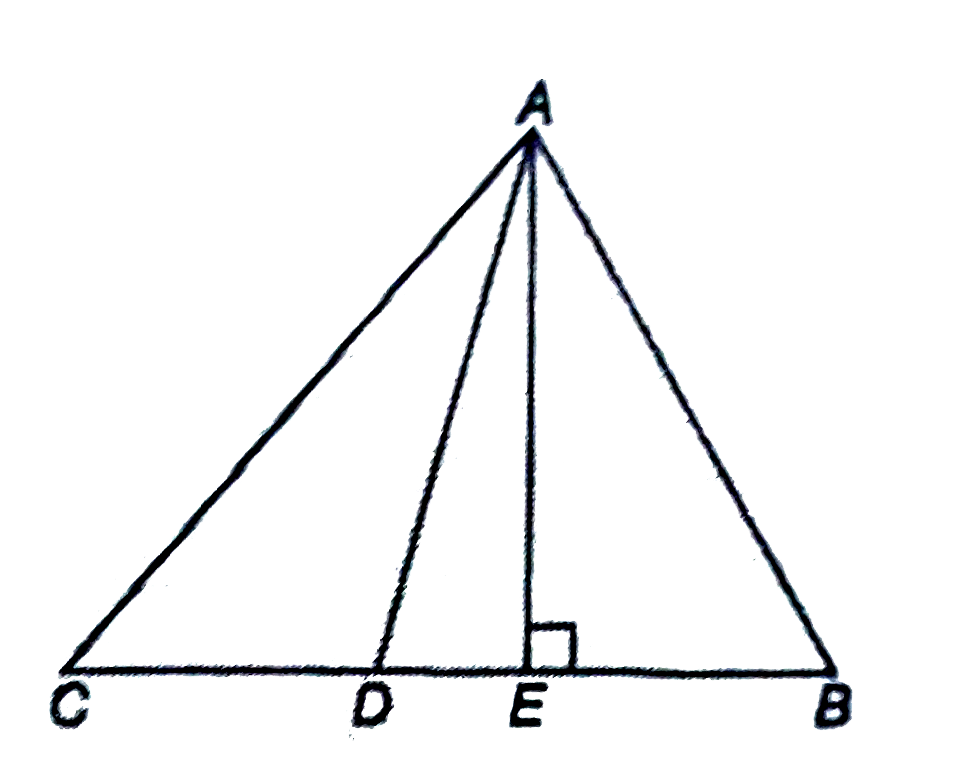
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .

View SolutionThe following figures shows a triangle ABC in which AD is median and AE⊥BC.
Prove that : 2AB2+2AC2=4AD2+BC2
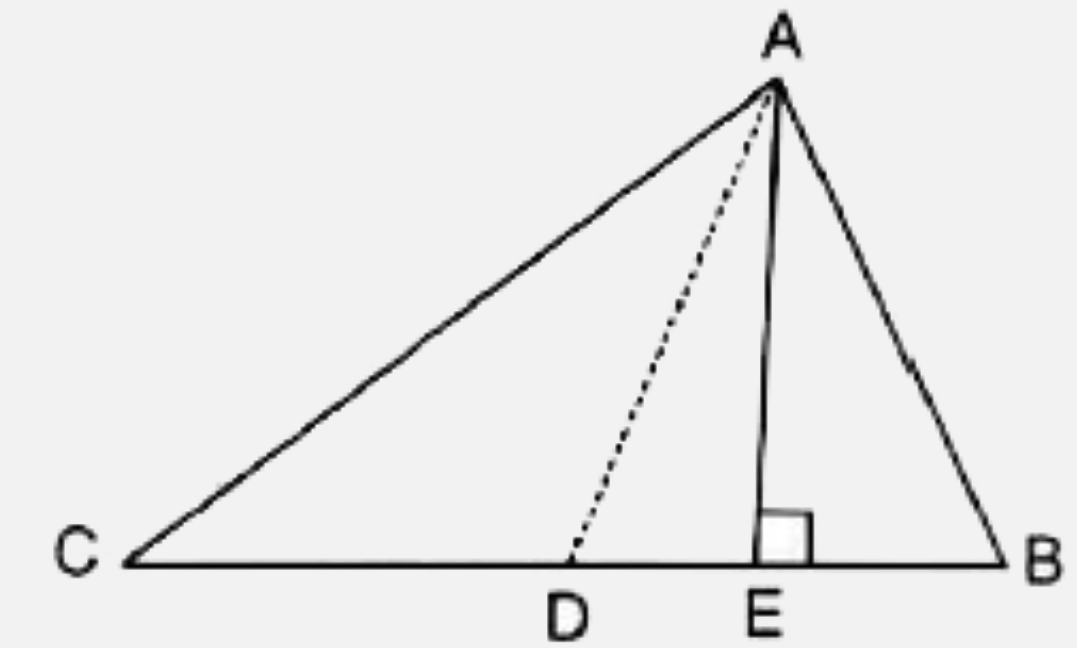
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that

AB2=BC×BD
View Solution
