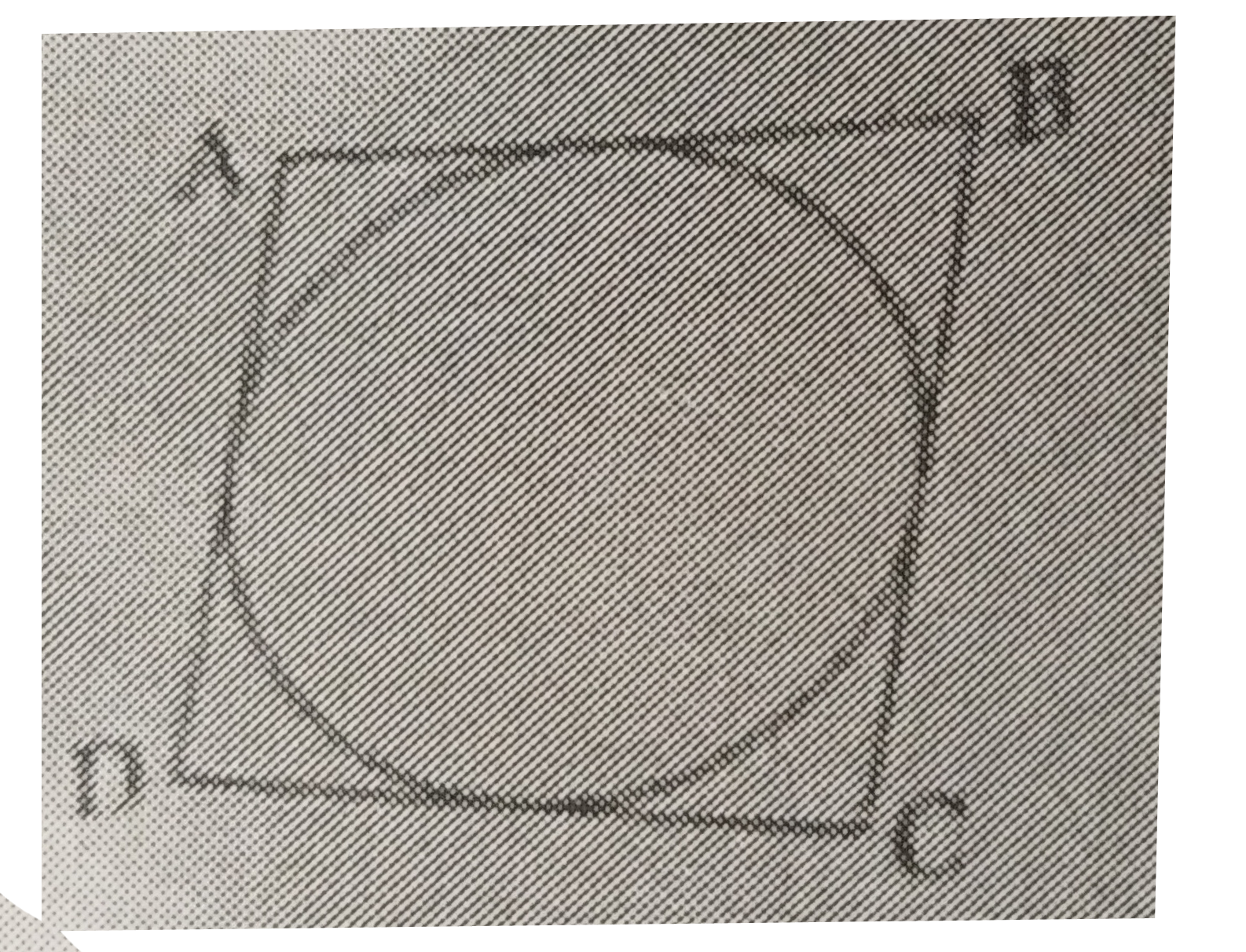
In Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
Step by step video solution for In Fig.2, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Constructions) (VERY SHORT ANSWER TYPE QUESTIONS)
2 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Constructions) (Long Answer Type Questions)
16 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Circles) (Very short Answer type questions)
6 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment
15 Videos
Similar Questions
Knowledge Check
A quadrilateral ABCD is drawn to circumscribe a circle such that its sides. AB , BC ,CD and DA touch the circle at P,Q,R and S , respectively . If AB = x cm BC = 7 cm , CR = 3 cm and AS = 5 cm , then x= ?
 A10 cmB8 cmC9 cmD7 cm
A10 cmB8 cmC9 cmD7 cmQuadrilateral ABCD is circumscribed to a circle. If AB=6cm, BC=7cm and CD=4cm then the length of AD is
A3cmB4cmC6cmD7cmIf the sides of a quadrilateral ABCD touch a circle and AB = 6 cm, CD = 5 cm, BC = 7 cm, then the length of AD in cm is :
A4 cmB5 cmC3 cmD6 cm
In figure, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3cm and AS = 5cm, then x = ______.

View SolutionA circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
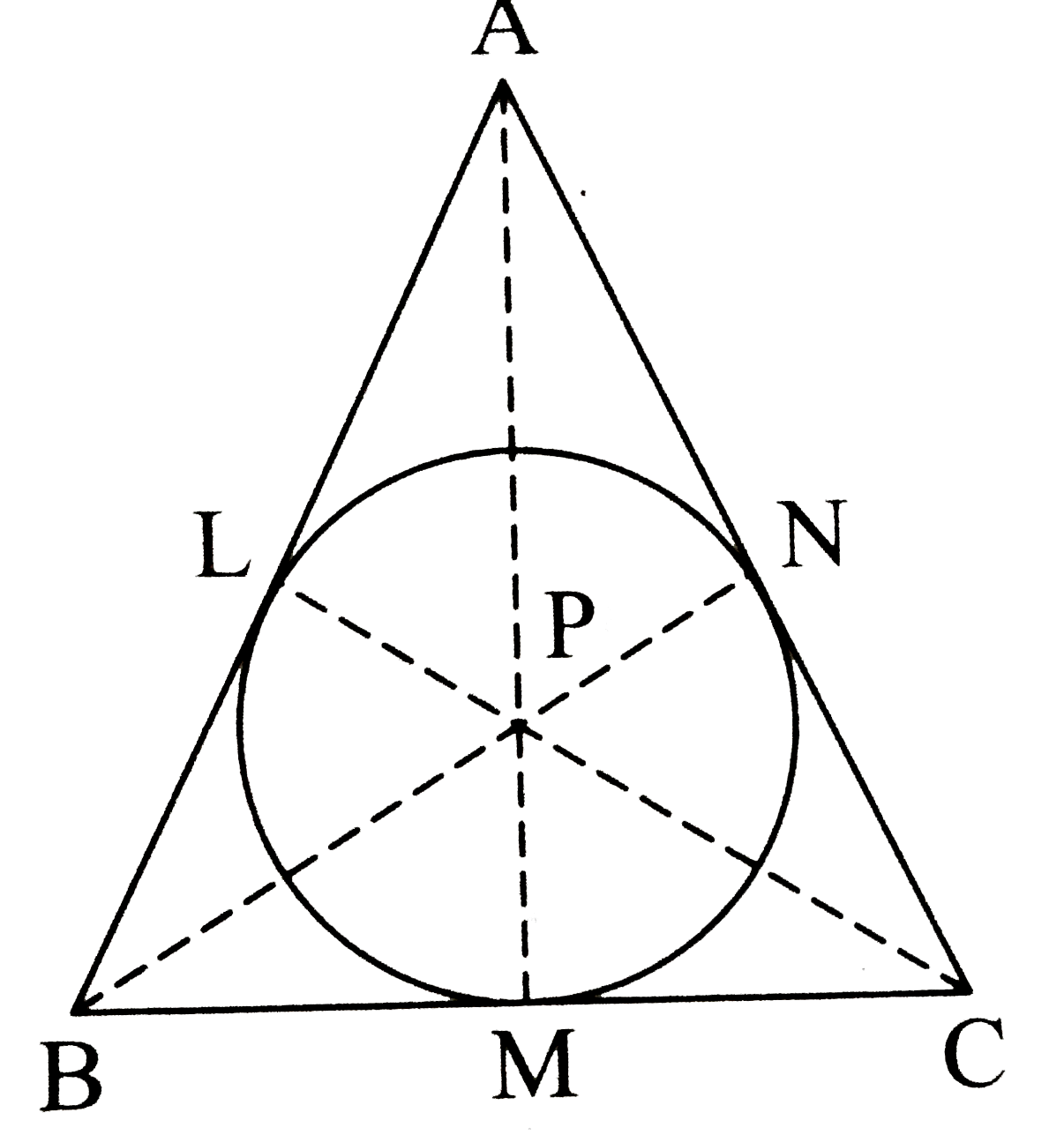
View SolutionThe sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P, Q, and R respectively.
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC.
or
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB+CD=BC+DA.
View SolutionA circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA
View Solution