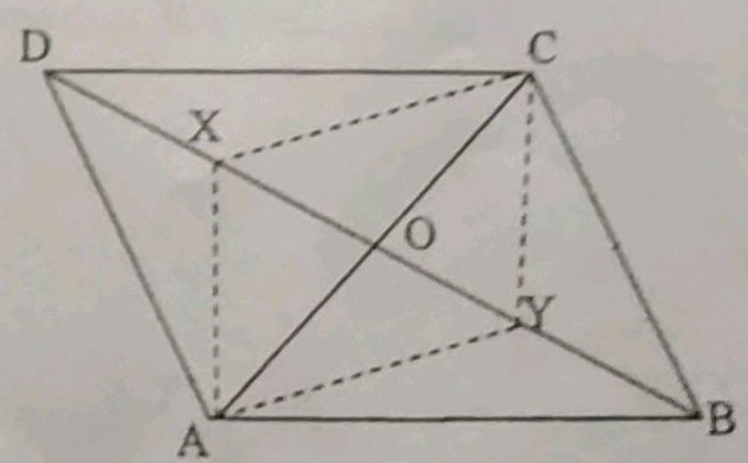
In Figure, is a parallelogram and are points on the diagonal such that . Prove that is a parallelogram (ii) (iv)
To prove the statements given in the question, we will follow these steps systematically.
Given:
- ABCD is a parallelogram.
- Points X and Y are on diagonal BD such that DX=BY.
To Prove:
1. AXCY is a parallelogram.
2. AX=CY and AY=CX.
3. △AYB≅△CXD.
4. △AXD≅△CYB.
Proof:
Step 1: Prove that AXCY is a parallelogram.
1. Consider triangles AYB and CXD:
- We know that AB∥CD (opposite sides of a parallelogram).
- Therefore, ∠AYB=∠CXD (alternate interior angles).
- Also, DX=BY (given).
- Lastly, AB=CD (opposite sides of a parallelogram).
By the criteria of congruence (ASA), we can conclude:
△AYB≅△CXD
Step 2: Show AY=CX.
From the congruence of triangles AYB and CXD, we have:
AY=CX
Step 3: Prove AX=CY.
2. Now consider triangles AXD and CYB:
- Again, AB∥CD implies ∠AXD=∠CYB (alternate interior angles).
- We know DX=BY (given).
- Also, AD=BC (opposite sides of a parallelogram).
By the criteria of congruence (ASA), we can conclude:
△AXD≅△CYB
Step 4: Show AX=CY.
From the congruence of triangles AXD and CYB, we have:
AX=CY
Step 5: Conclude that AXCY is a parallelogram.
Since we have shown:
- AX=CY
- AY=CX
This means that both pairs of opposite sides are equal, which proves that AXCY is a parallelogram.
Final Statements:
1. AXCY is a parallelogram.
2. AX=CY and AY=CX.
3. △AYB≅△CXD.
4. △AXD≅△CYB.
- ABCD is a parallelogram.
- Points X and Y are on diagonal BD such that DX=BY.
1. AXCY is a parallelogram.
2. AX=CY and AY=CX.
3. △AYB≅△CXD.
4. △AXD≅△CYB.
- We know that AB∥CD (opposite sides of a parallelogram).
- Therefore, ∠AYB=∠CXD (alternate interior angles).
- Also, DX=BY (given).
- Lastly, AB=CD (opposite sides of a parallelogram).
By the criteria of congruence (ASA), we can conclude:
△AYB≅△CXD
AY=CX
- Again, AB∥CD implies ∠AXD=∠CYB (alternate interior angles).
- We know DX=BY (given).
- Also, AD=BC (opposite sides of a parallelogram).
By the criteria of congruence (ASA), we can conclude:
△AXD≅△CYB
AX=CY
- AX=CY
- AY=CX
1. AXCY is a parallelogram.
2. AX=CY and AY=CX.
3. △AYB≅△CXD.
4. △AXD≅△CYB.
Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
 View Solution
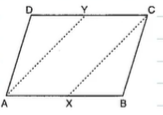
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
 View Solution
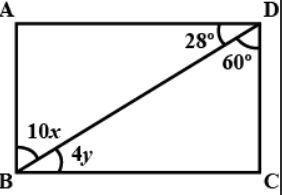
View SolutionIn Figure, ABCD is a parallelogram. Compute the values of x and y
 View Solution
View SolutionIn a ABC median AD is produced to X such that AD=DX . Prove that ABXC is a parallelogram.
View SolutionABCD is a parallelogram and line segments AX,CY bisect the angles AandC, respectively. Show that AX∣∣CY
View SolutionABCD is a parallelogram X and Y are the mid-points of BC and CD respectively. Prove that ar(AXY)=38ar(∣∣gmABCD)
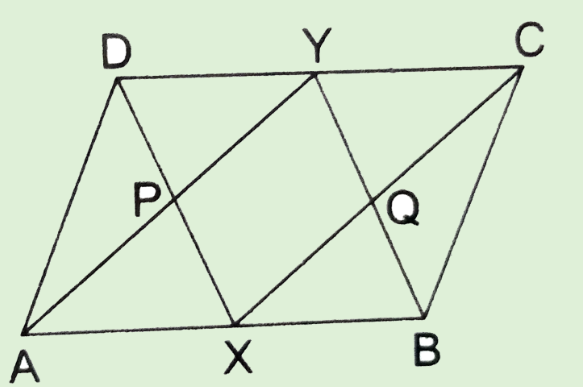
View SolutionIn Figure, X, Y are the mid-points of opposite sides AB and DC of a parallelogram ABCD.AY and DX are joined intersecting in P;CX and BY are joined intersecting in Q . Show that AXCY is a parallelogram (ii) DXBY is a parallelogram quadrilateral PXQY is a parallelogram
 View Solution
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View SolutionABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionABCD is a trapezium with AB∣∣DC . A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View Solution

