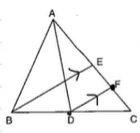
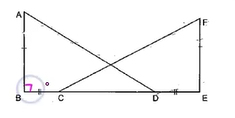
In Figure, AD and BE
are medians of ABC and BE∣∣DF
. Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14AC
Topper's Solved these Questions
Similar Questions
In Figure, AD, and BE are medians of ABC and BE∣∣DF. Prove that CF=14AC.
 View Solution
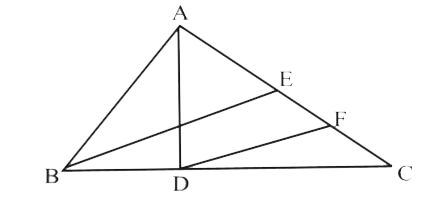
View SolutionIn the given figure AD and BE are the medians of ΔABC and BE || DF . Prove that CF=1/4AC.
 View Solution
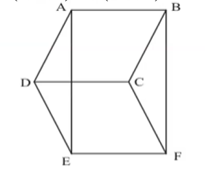
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
 View Solution
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
 View Solution
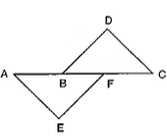
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE= ≅CBD
 View Solution
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).
 View Solution
View SolutionThe AD,BEandCF are the medians of a cABC, then (AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
View SolutionIn Fig. 4.101, AD and CE are two altitudes of ABC . Prove that AEF~CDF (ii) ABD~CBE (iii) AEF~ADB (iv) FDC~BEC (FIGURE)
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
 View Solution
View Solution

