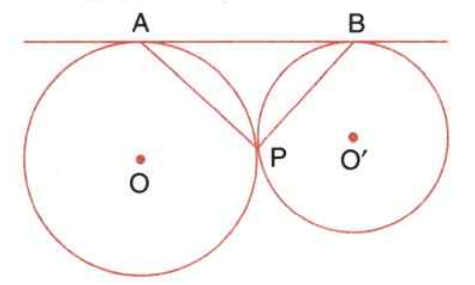
In figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB=CD

Given AB and CD are common tangent to two circles of unequal radius
To prove AB=CD

Construction Produce AB and CD, to intersect at P.
Proof PA=PC
[the length of tangents drawn from an internal point to a circle are equal]
Also, PB=PD
[the lengths of tangents drawn from an internal point to a circle are equal]
∴PA−PB=PC−PD
AB=CD Hence proved.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS14videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.2 VERY SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure, AB and CD are the diameters of the circle. What is the value of x?
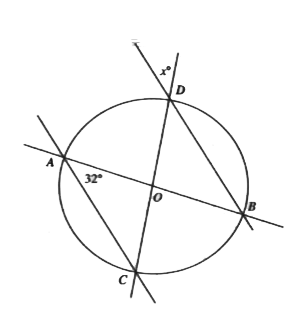 A16∘B18∘C26∘D32∘
A16∘B18∘C26∘D32∘ - Question 2 - Select One
Column Ain the figure, P and Q are center of the two circle of radii 3 and 4 respectively. A and B are the points at which a common tangent touches each circleColumn BABPQ
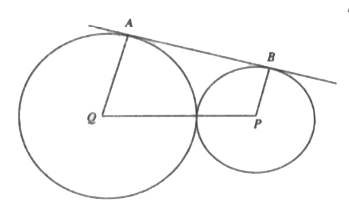 AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.
 View Solution
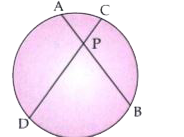
View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
 View Solution
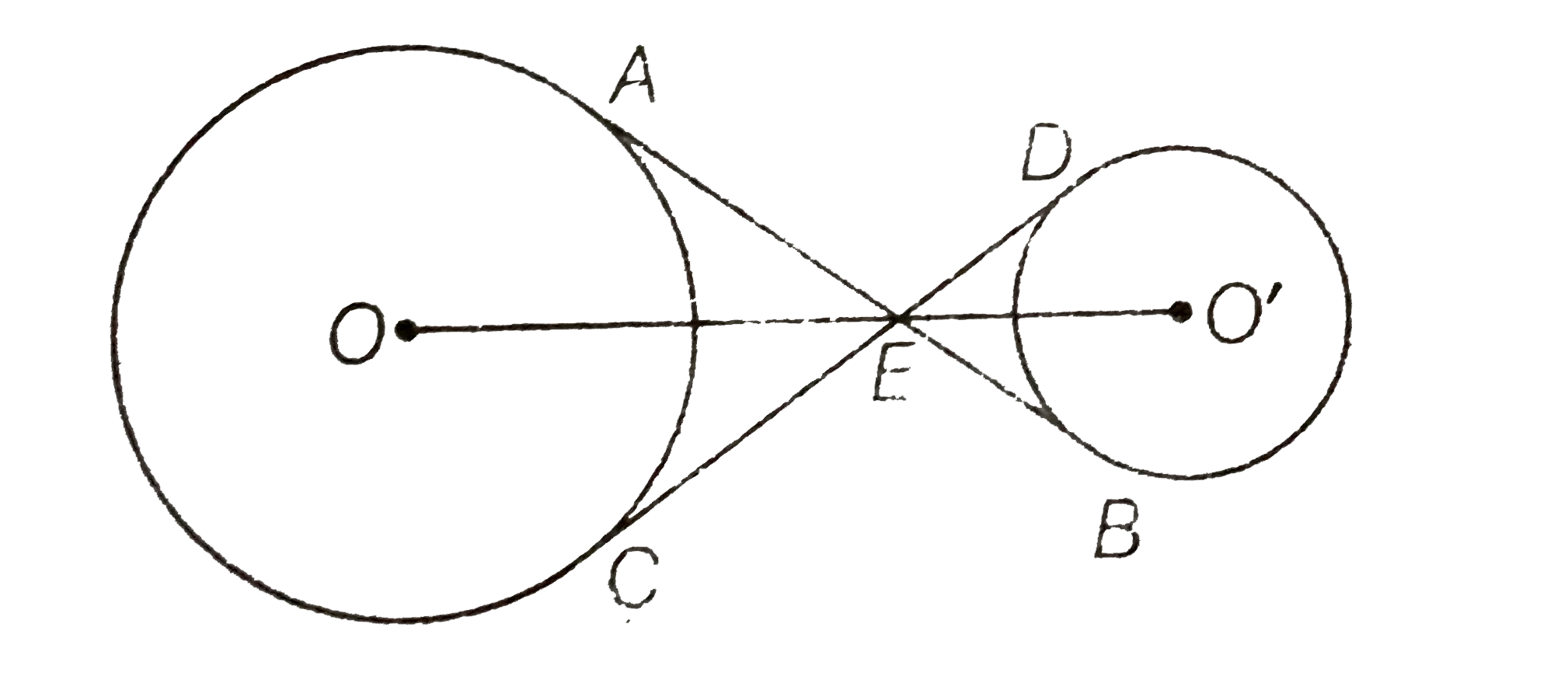
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
 View Solution
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
 View Solution
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
 View Solution
View SolutionIn the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
(i) tangent at point P bisects AB
(ii) angle APB=90∘View Solution



