In Figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘
OC=OD=CD
equilateral triangle
∠COD=600
∠COD=2∠CBD
∠CBD=300
∠ECB=900
In ∠ECB
∠ECB+∠CBE+∠CEB=1800
∠CEB=1800
∠CEB=180−90−30=600.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 10.2
2 Videos
- CIRCLESBOOK - NCERT ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.3
3 Videos
- CIRCLESBOOK - NCERT ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 10.5
11 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERT ENGLISHCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Solved Examples
4 Videos
- CONSTRUCTIONSBOOK - NCERT ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE 11.2
5 Videos
Similar Questions
In the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionAB is a diameter of a circle C(O, r). Chord CD is equal to radius OC. If AC and BD when produced intersect at P, prove that ∠APB is constant.
View SolutionAB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB=60∘
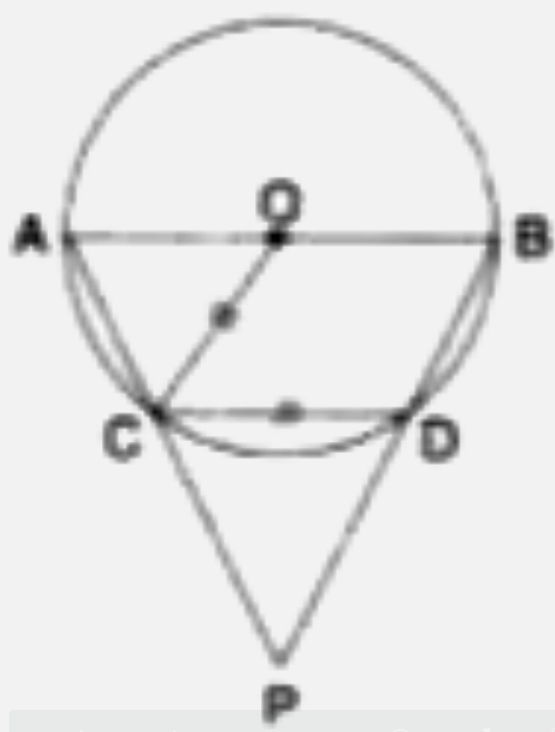
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
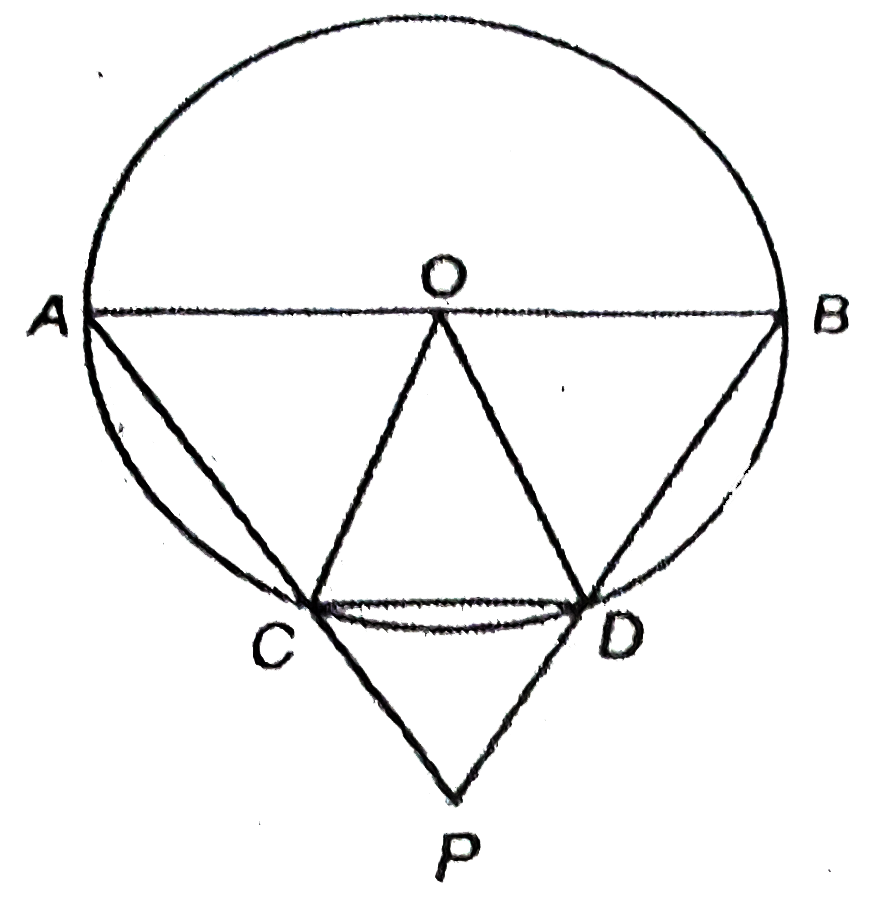
View SolutionABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB=60∘ .
View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View SolutionThe given figure shows, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that:
AB2=AC×AP
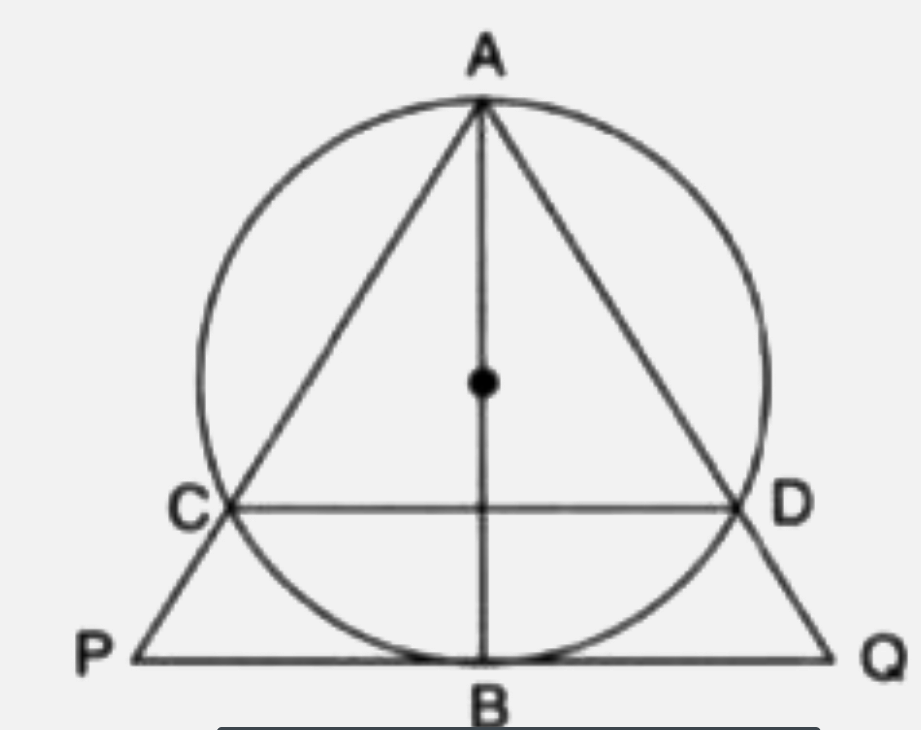
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View Solution
