AB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
To solve the problem, we will follow these steps systematically:
Step 1: Draw the Circle and Label Points
- Draw a circle with diameter AB. Let O be the center of the circle.
- Mark points A and B on the circle such that AB is the diameter.
- Draw chord AC such that angle BAC = 30°.
- Extend line AB to point D where the tangent at point C intersects.
Hint: Remember that a diameter divides the circle into two equal halves.
Step 2: Identify Angles
- Since AB is the diameter, angle ACB is a right angle (90°) because the angle inscribed in a semicircle is always 90°.
- We have angle BAC = 30°.
Hint: Use the property of angles in a semicircle to find angle ACB.
Step 3: Calculate Angle CBA
- In triangle ABC, the sum of angles is 180°.
- Therefore, angle ACB + angle BAC + angle CBA = 180°.
- Substitute the known values: 90° + 30° + angle CBA = 180°.
- This simplifies to angle CBA = 180° - 120° = 60°.
Hint: Remember the triangle angle sum property: the sum of angles in a triangle is always 180°.
Step 4: Use Linear Pair to Find Angle CBD
- Since D is on the extended line AB, angle CBA + angle CBD = 180°.
- Substitute the known value: 60° + angle CBD = 180°.
- Thus, angle CBD = 180° - 60° = 120°.
Hint: A linear pair of angles on a straight line always sums to 180°.
Step 5: Apply Alternate Segment Theorem
- By the alternate segment theorem, angle BCD = angle BAC = 30°.
Hint: Recall that the alternate segment theorem states that the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
Step 6: Calculate Angle DBC in Triangle CBD
- In triangle CBD, the sum of angles is 180°.
- Therefore, angle CDB + angle BCD + angle DBC = 180°.
- Substitute the known values: angle CDB + 30° + 120° = 180°.
- This simplifies to angle CDB = 180° - 150° = 30°.
Hint: Use the triangle angle sum property again to find the missing angle.
Step 7: Conclude that BC = BD
- In triangle CBD, we have angle DBC = 30° and angle CDB = 30°.
- Since two angles are equal, the sides opposite those angles are also equal (BC = BD).
Hint: Remember that in a triangle, if two angles are equal, the sides opposite those angles are also equal.
Final Answer
Thus, we conclude that BC = BD.
---
- Draw a circle with diameter AB. Let O be the center of the circle.
- Mark points A and B on the circle such that AB is the diameter.
- Draw chord AC such that angle BAC = 30°.
- Extend line AB to point D where the tangent at point C intersects.
- Since AB is the diameter, angle ACB is a right angle (90°) because the angle inscribed in a semicircle is always 90°.
- We have angle BAC = 30°.
- In triangle ABC, the sum of angles is 180°.
- Therefore, angle ACB + angle BAC + angle CBA = 180°.
- Substitute the known values: 90° + 30° + angle CBA = 180°.
- This simplifies to angle CBA = 180° - 120° = 60°.
- Since D is on the extended line AB, angle CBA + angle CBD = 180°.
- Substitute the known value: 60° + angle CBD = 180°.
- Thus, angle CBD = 180° - 60° = 120°.
- By the alternate segment theorem, angle BCD = angle BAC = 30°.
- In triangle CBD, the sum of angles is 180°.
- Therefore, angle CDB + angle BCD + angle DBC = 180°.
- Substitute the known values: angle CDB + 30° + 120° = 180°.
- This simplifies to angle CDB = 180° - 150° = 30°.
- In triangle CBD, we have angle DBC = 30° and angle CDB = 30°.
- Since two angles are equal, the sides opposite those angles are also equal (BC = BD).
Thus, we conclude that BC = BD.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
In the given figure AB is the diameter and AC is the chord of a circle such that ∠BAC=30∘. The tangent at C intersects AB produced at D. Prove that :BC=BD.
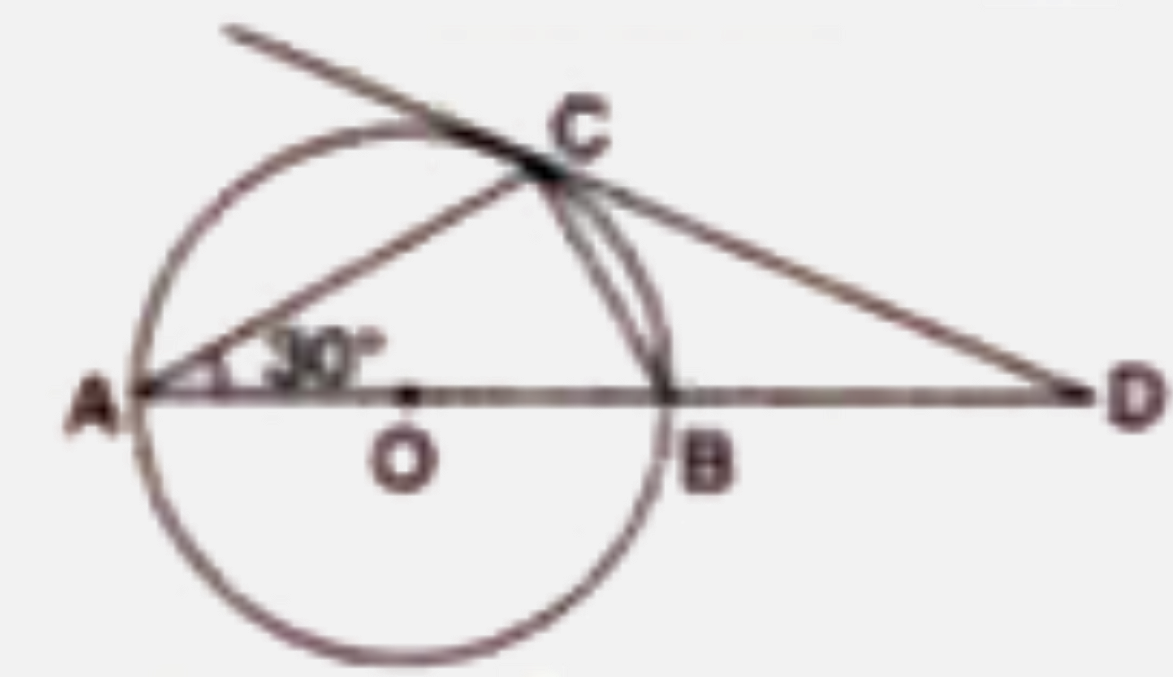 View Solution
View SolutionIn figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
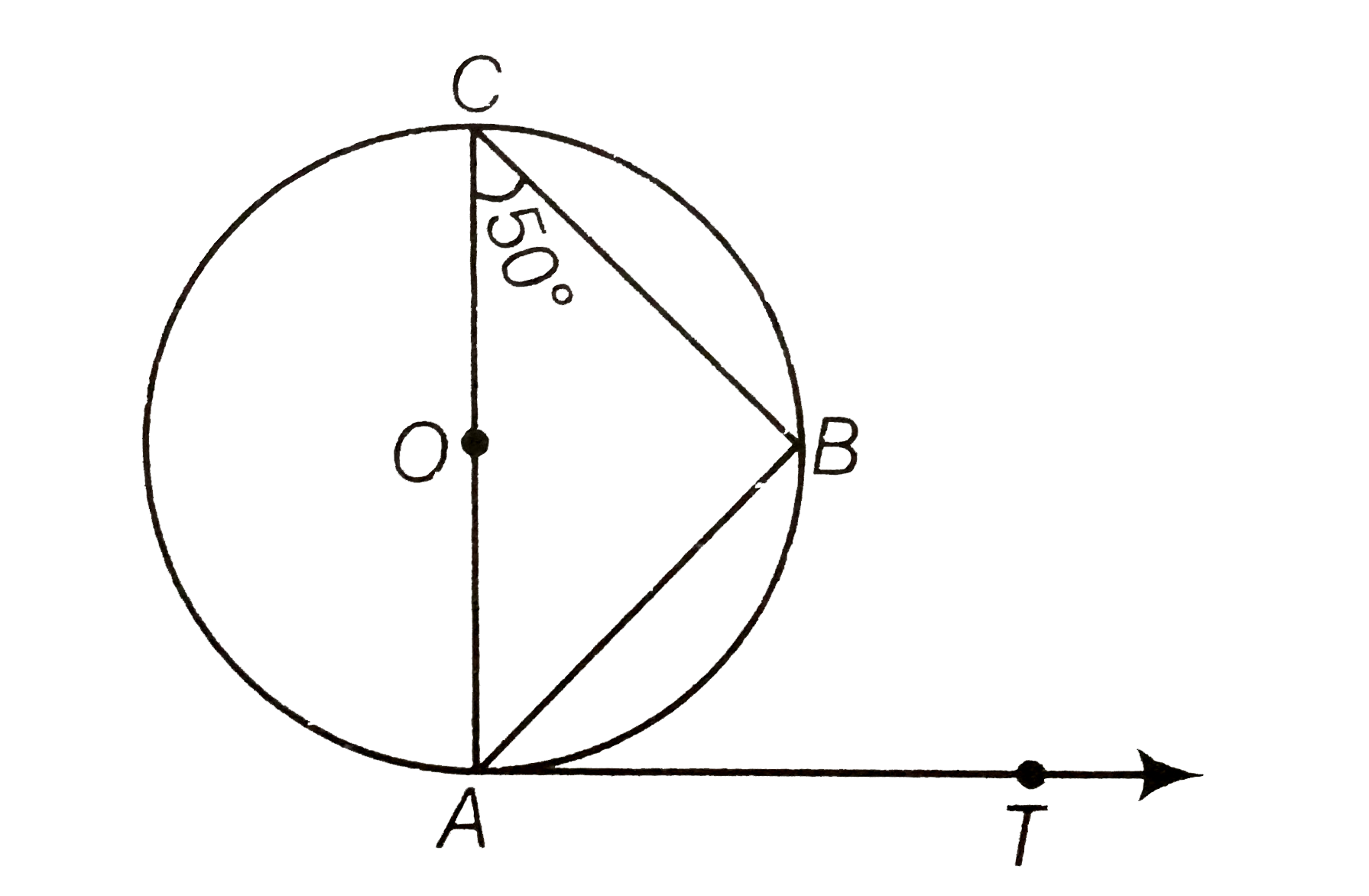 View Solution
View SolutionIn figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then angleBAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View SolutionIf AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.
 View Solution
View SolutionIn Figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘
View SolutionAD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
View SolutionIn the adjoining figure, O is the centre of the circle and AC is its diameter. If ∠BAC=30∘, then find ∠BOC.
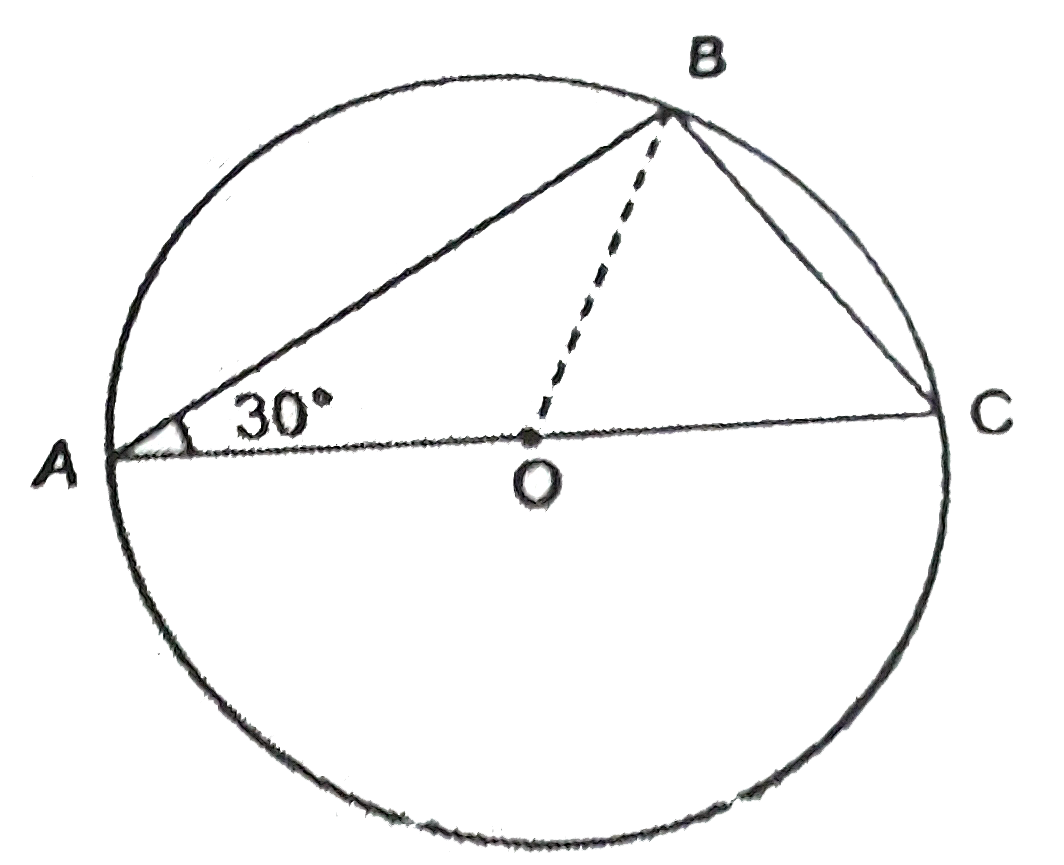 View Solution
View Solution

