In Figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘
To solve the problem step by step, we will use the properties of circles and triangles.
Step 1: Understand the Given Information
- AB is the diameter of the circle.
- CD is a chord equal to the radius of the circle.
- AC and BD when extended intersect at point E.
Step 2: Identify the Key Properties
Since AB is the diameter, we know that angle ACB is a right angle (90 degrees) because of the angle in a semicircle theorem.
Step 3: Analyze Triangle OCD
Since CD is equal to the radius of the circle, we have:
- OC = OD = CD (all are equal to the radius of the circle).
This implies that triangle OCD is an equilateral triangle, where all sides are equal.
Step 4: Calculate Angle COD
In an equilateral triangle, all angles are equal. Therefore:
- Angle COD = 60 degrees.
Step 5: Relate Angle COD to Angle CBD
Angle COD subtends arc CD at the center O and angle CBD at point B. By the inscribed angle theorem:
- Angle COD = 2 * angle CBD.
Thus:
- 60∘=2∗angleCBD
- Therefore, angleCBD=60∘2=30∘.
Step 6: Calculate Angle ACB
Since AB is the diameter:
- Angle ACB = 90 degrees (angle in a semicircle).
Step 7: Find Angle BCE
Angles ACB and BCE are a linear pair:
- angleACB+angleBCE=180∘.
Thus:
- 90∘+angleBCE=180∘.
So:
- angleBCE=180∘−90∘=90∘.
Step 8: Analyze Triangle ECB
In triangle ECB, the sum of angles is 180 degrees:
- angleCEB+angleECB+angleCBE=180∘.
Substituting known values:
- angleCEB+90∘+30∘=180∘.
This simplifies to:
- angleCEB+120∘=180∘.
Thus:
- angleCEB=180∘−120∘=60∘.
Conclusion
We have proved that:
- angleAEB=60∘.
- AB is the diameter of the circle.
- CD is a chord equal to the radius of the circle.
- AC and BD when extended intersect at point E.
Since AB is the diameter, we know that angle ACB is a right angle (90 degrees) because of the angle in a semicircle theorem.
Since CD is equal to the radius of the circle, we have:
- OC = OD = CD (all are equal to the radius of the circle).
This implies that triangle OCD is an equilateral triangle, where all sides are equal.
In an equilateral triangle, all angles are equal. Therefore:
- Angle COD = 60 degrees.
Angle COD subtends arc CD at the center O and angle CBD at point B. By the inscribed angle theorem:
- Angle COD = 2 * angle CBD.
Thus:
- 60∘=2∗angleCBD
- Therefore, angleCBD=60∘2=30∘.
Since AB is the diameter:
- Angle ACB = 90 degrees (angle in a semicircle).
Angles ACB and BCE are a linear pair:
- angleACB+angleBCE=180∘.
Thus:
- 90∘+angleBCE=180∘.
So:
- angleBCE=180∘−90∘=90∘.
In triangle ECB, the sum of angles is 180 degrees:
- angleCEB+angleECB+angleCBE=180∘.
Substituting known values:
- angleCEB+90∘+30∘=180∘.
This simplifies to:
- angleCEB+120∘=180∘.
Thus:
- angleCEB=180∘−120∘=60∘.
We have proved that:
- angleAEB=60∘.
Topper's Solved these Questions
Similar Questions
In the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionAB is a diameter of a circle C(O, r). Chord CD is equal to radius OC. If AC and BD when produced intersect at P, prove that ∠APB is constant.
View SolutionAB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB=60∘
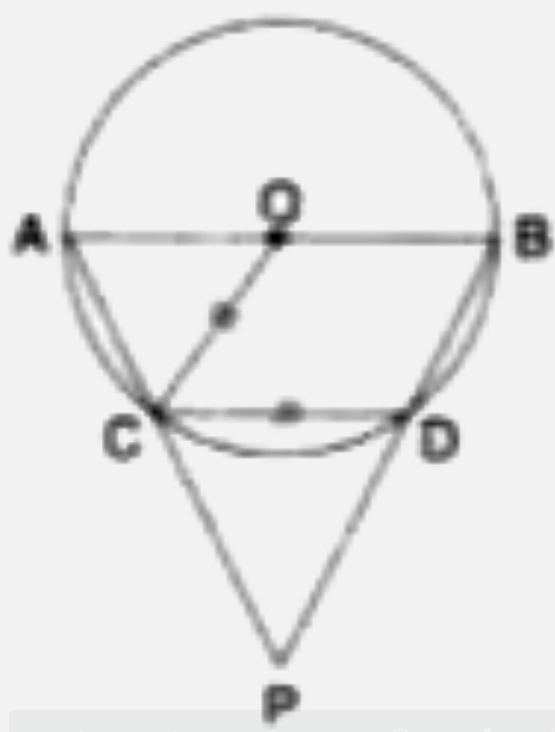
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
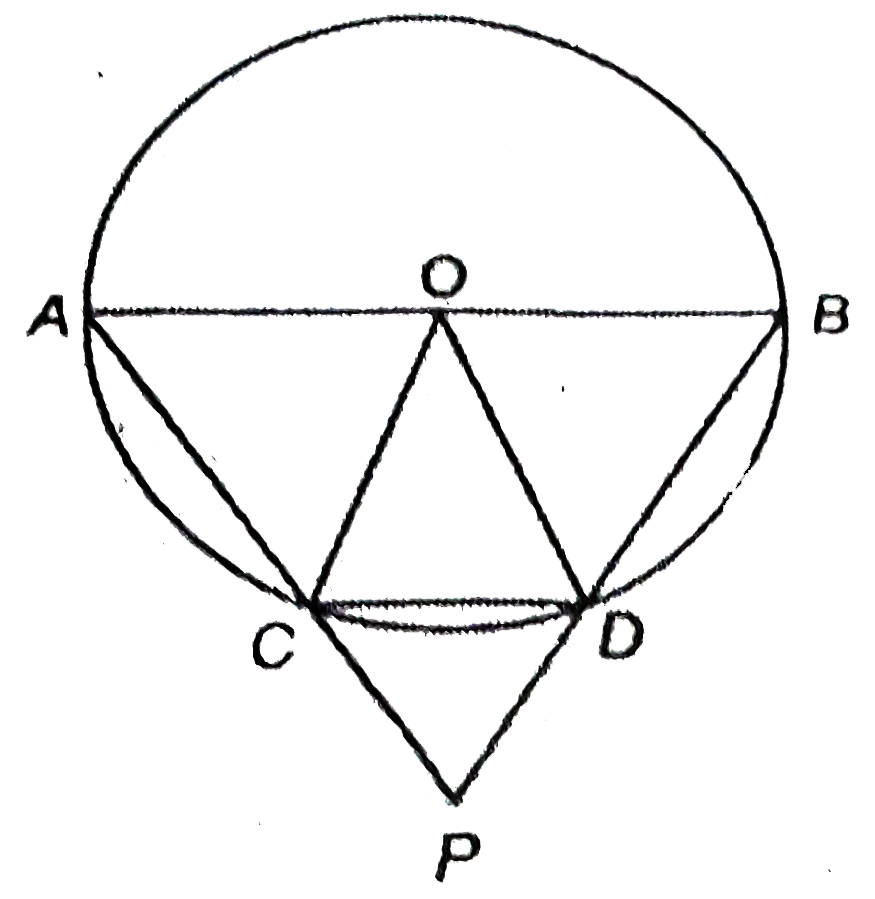
View SolutionABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB=60∘ .
View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

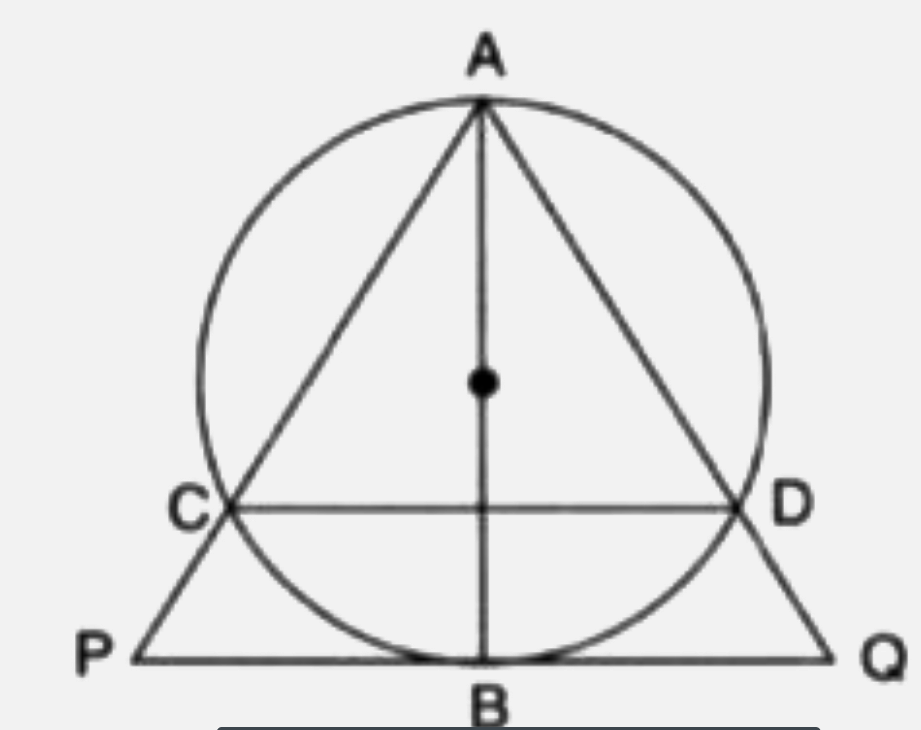
View SolutionThe given figure shows, AB is a diameter of the circle. Chords AC and AD produced meet the tangent to the circle at point B in points P and Q respectively. Prove that:
AB2=AC×AP
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View Solution
