In figure, AB||DE, AB=DE, AC||DF and AC=DF. Prove that BC||EF and BC=EF.
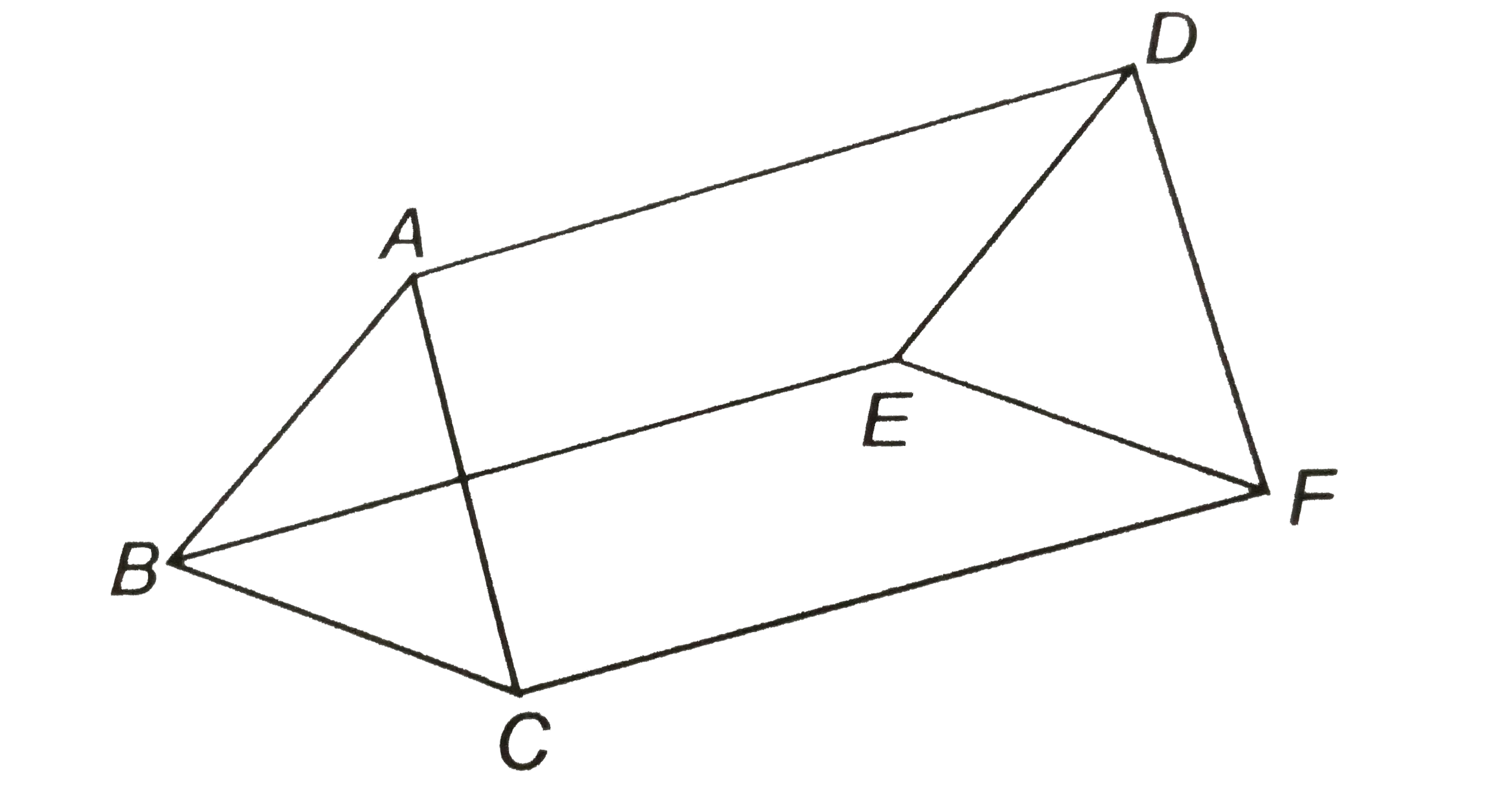
Given: AB||DE.AB=DE,AC||DFandAC||=DFTo prove:BC||EFandBC=EF Proof:
Prove: AC||DF (given)
and AC=DF (given)
∴ACFD is a parallelogram.
⇒ AD||CF (∵opposite sides of a parallelogram are parallel)...(1)
and AD||CF (∵opposite sides of a parallelogram are equal)...(2)
Now, AB||DE (given)
and AB||DE (given)
∴ ABED is a parallelogram.
⇒ AD||BE (∵opposite sides of a parallelogram are parallel)...(3)
⇒ AD=BE (∵opposite sides of a parallelogram are equal)...(4)
From (1) and (3), we get
CF||BE
And, from (2) and (4), we get
CF=BE
∴ BCEF is a parallelogram.
⇒ BC||EF (∵opposite sides of a parallelogram are parallel)
⇒ BC=EF (∵opposite sides of a parallelogram are equal)
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b
15 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)
5 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
In figure, DE||ABandBD||BEF. Prove that DC2=CF×AC
View SolutionIn the given figure, if DE||AQ and DF||AR. Prove that EF||QR.

View SolutionIn Figure DE||BC and CD||EF. Prove that AD2=AB⋅AF.
View SolutionIn the given figure, AC=AE,AB=AD and ∠BAD=∠EAC. Prove that BC=DE.
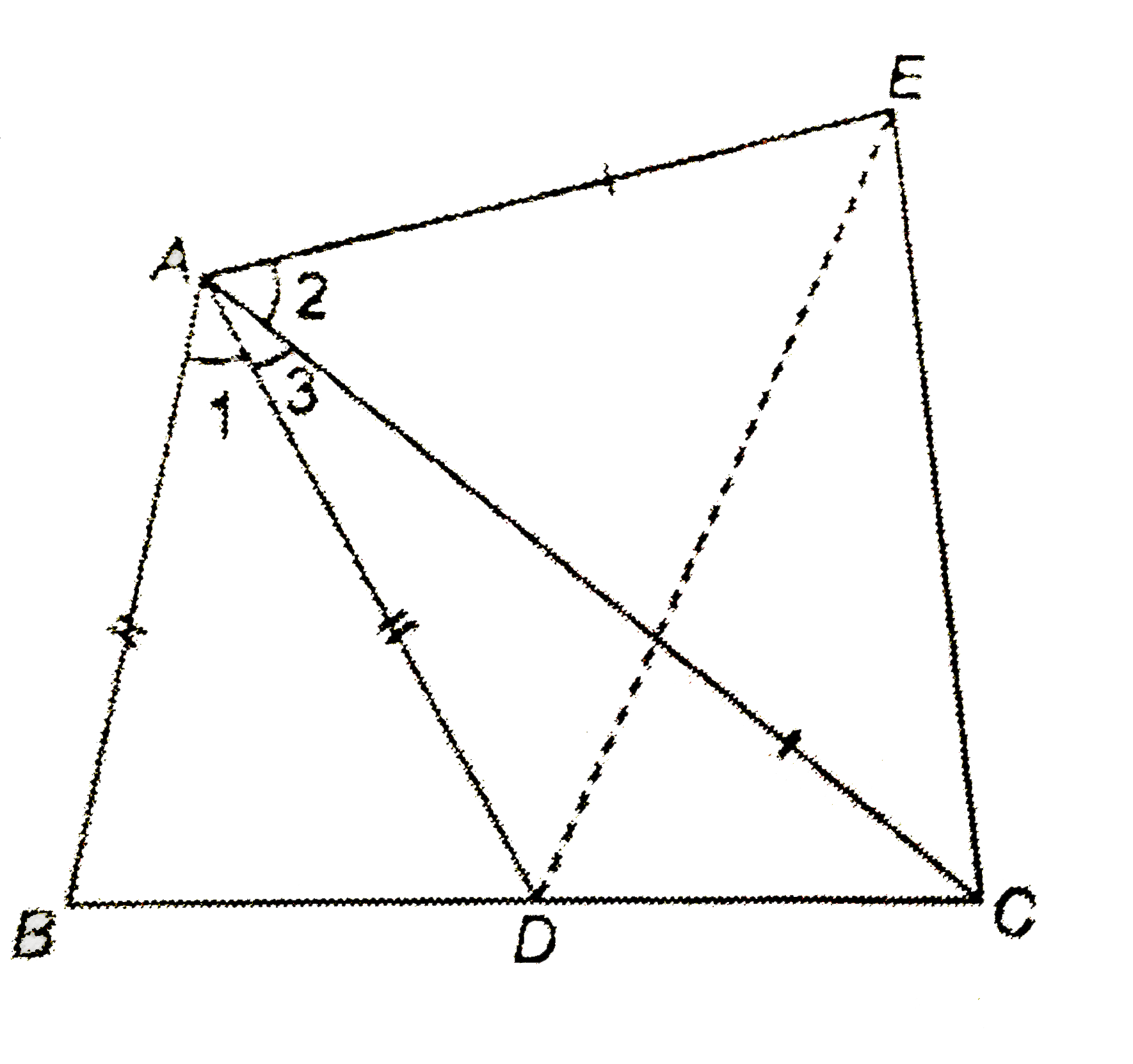
View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC

View SolutionIn the adjoining figure, AB=EF,BC=DE,∠ABC=∠FED=90∘, prove that AD=CF.
View SolutionIn a given figure, AB//DC//EF,AD//BEandDE//AF. Prove that the area of prallelogram DEFH is equal to the area of parallelogram ABCD.

View SolutionIn a given figure, AB//DC//EF,AD//BEandDE//AF. Prove that the area of prallelogram DEFH is equal to the area of parallelogram ABCD.

View SolutionIn the given figure D is mid-point of AB. DE//BC and DF //AC . Prove that : DE = BF

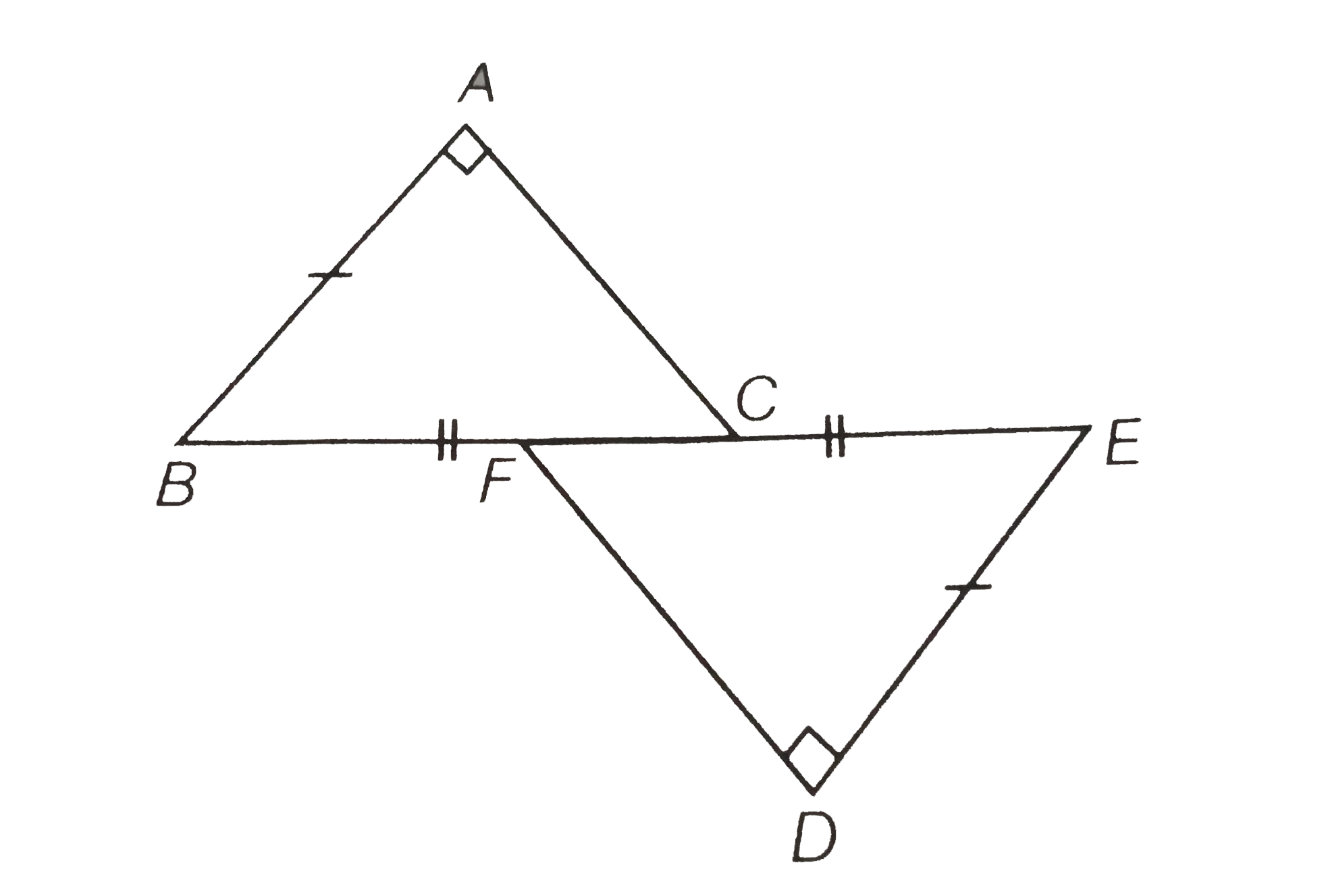
View SolutionIn figure ,BA⊥AC,DE⊥DF such that BA = DE and BF = EC. Show that ΔABC≅ΔDEF.
View Solution
