In figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
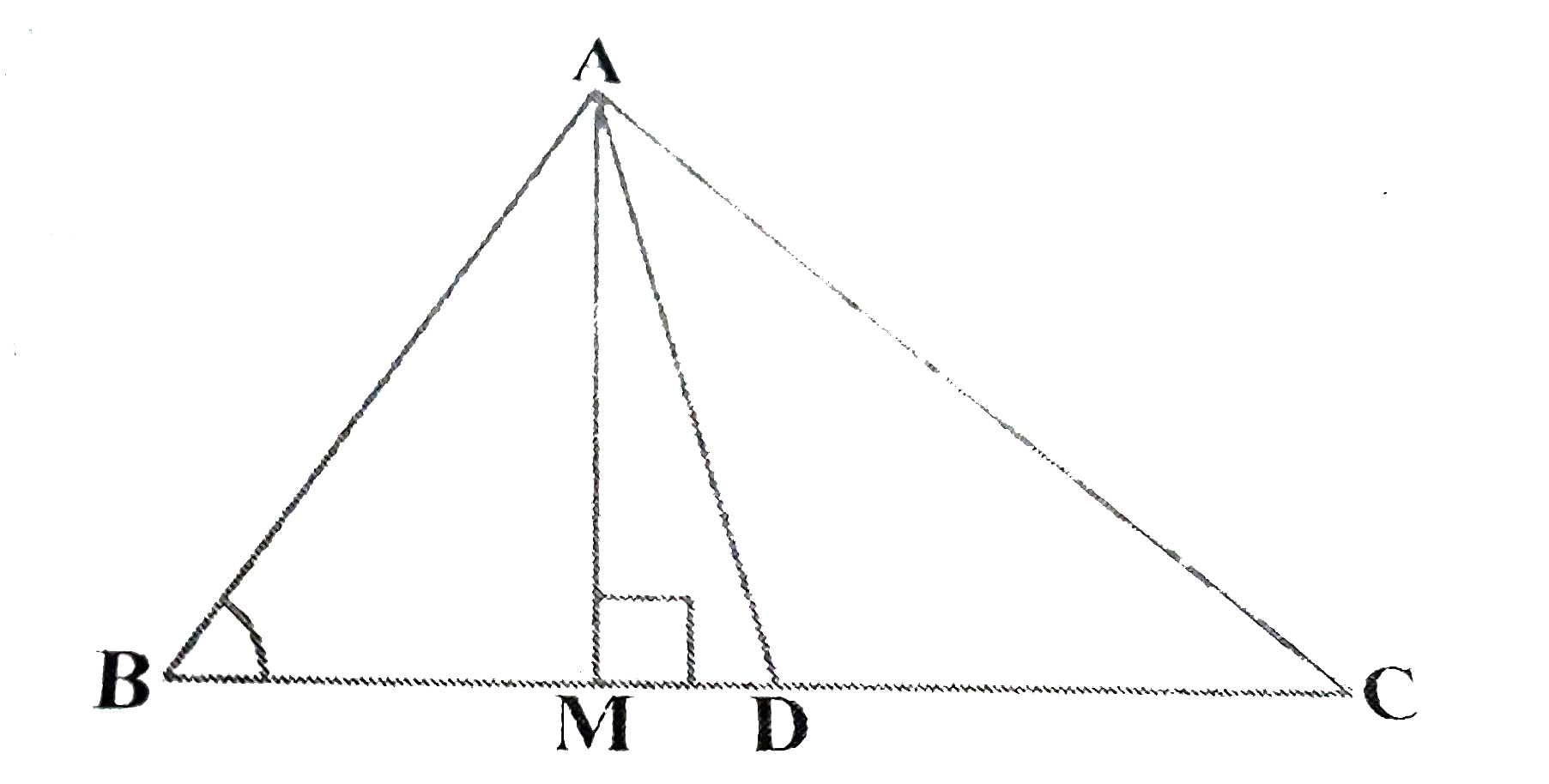
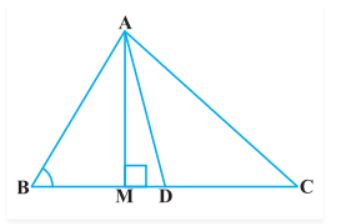
Given:
In ΔABC,ADis a median, AM⊥BC.
To Prove
(i) (AC)2=(AD)2+BC.DM+(BC2)2
(ii) (AB)2=(AD)2–BC.DM+(BC2)2
(iii) (AC)2+(AB)2=2(AD)2+12(BC)2
Proof:
i) In obtuse ΔADC,∠D>90∘
(AC)2=(AD)2+(DC)2+2DC.DM
(AC)2=(AD)2+(BC2)2+2(BC2).DM
(AC)2=(AD)2+(BC2)2+BC.DM
Or (AC)2=(AD)2+BC.DM+(BC2)2
II)In acute triangle ABD,
∠D>90∘
(AB)2=(AD)2+(BD)2+2BD.DM
(AB)2=(AD)2+(BC2)2−2(BC2).DM
(AB)2=(AD)2+(BC2)2−BC.DM
Or
(AB)2=(AD)2−BC.DM+(BC2)2
iii) Adding i and ii
(AC)2+(AB)2=(AD)2+BC.DM+(BC2)2+(AD)2−BC.DM+(BC2)2
=2(AD)2+BC42+BC42
=2(AD)2+12.BC42
=2(AD)2+(BC)2
Topper's Solved these Questions
Similar Questions
In figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn Figure, ∠B of ABC is an acute angle and AD⊥BC , prove that AC2=AB2+BC2−2 BC×BD
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
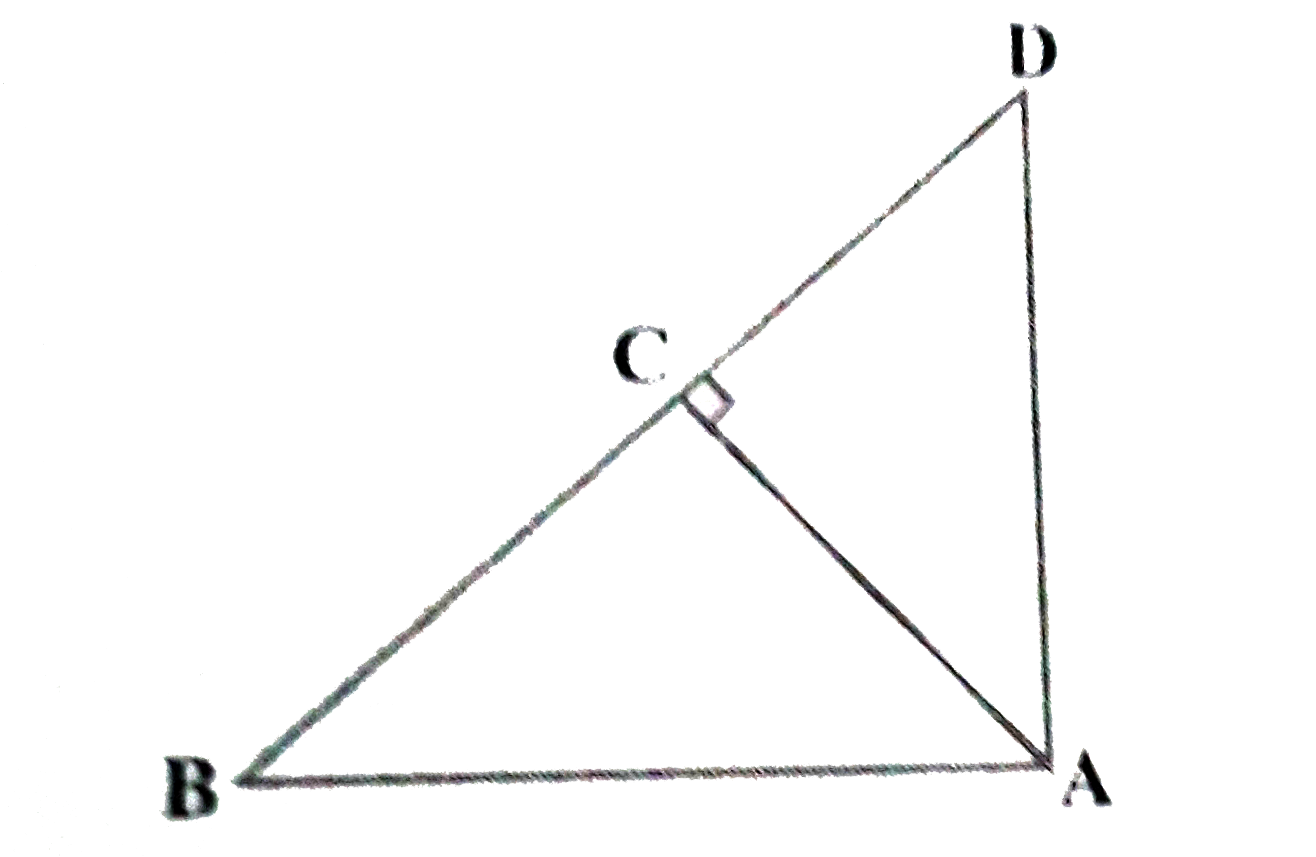
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BC.DE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BC⋅DE+14BC2
View SolutionIn figure, ABC is triangle in which ∠ABC>90∘ and AD⊥CBproduced. Prove that AC2=AB2+BC2+2BC.BD.

View SolutionIn an equilateral ABC , AD⊥BC , prove that AD2=3 BD2
View SolutionIn fig., if AD⊥BC, prove thatAB2+CD2=BD2+AC2.
View SolutionIn Figure, AD⊥BC and BD=13CD. Prove that 2CA2=2AB2+BC2
View SolutionIn Figure, ABC is an obtuse triangle, obtuse angled at B . If AD⊥CB , prove that AC2=AB2+BC2+2 BC×BD .
View Solution
