In figure, altitudes YZ and XT of intersect at P. Prove that
is cyclic
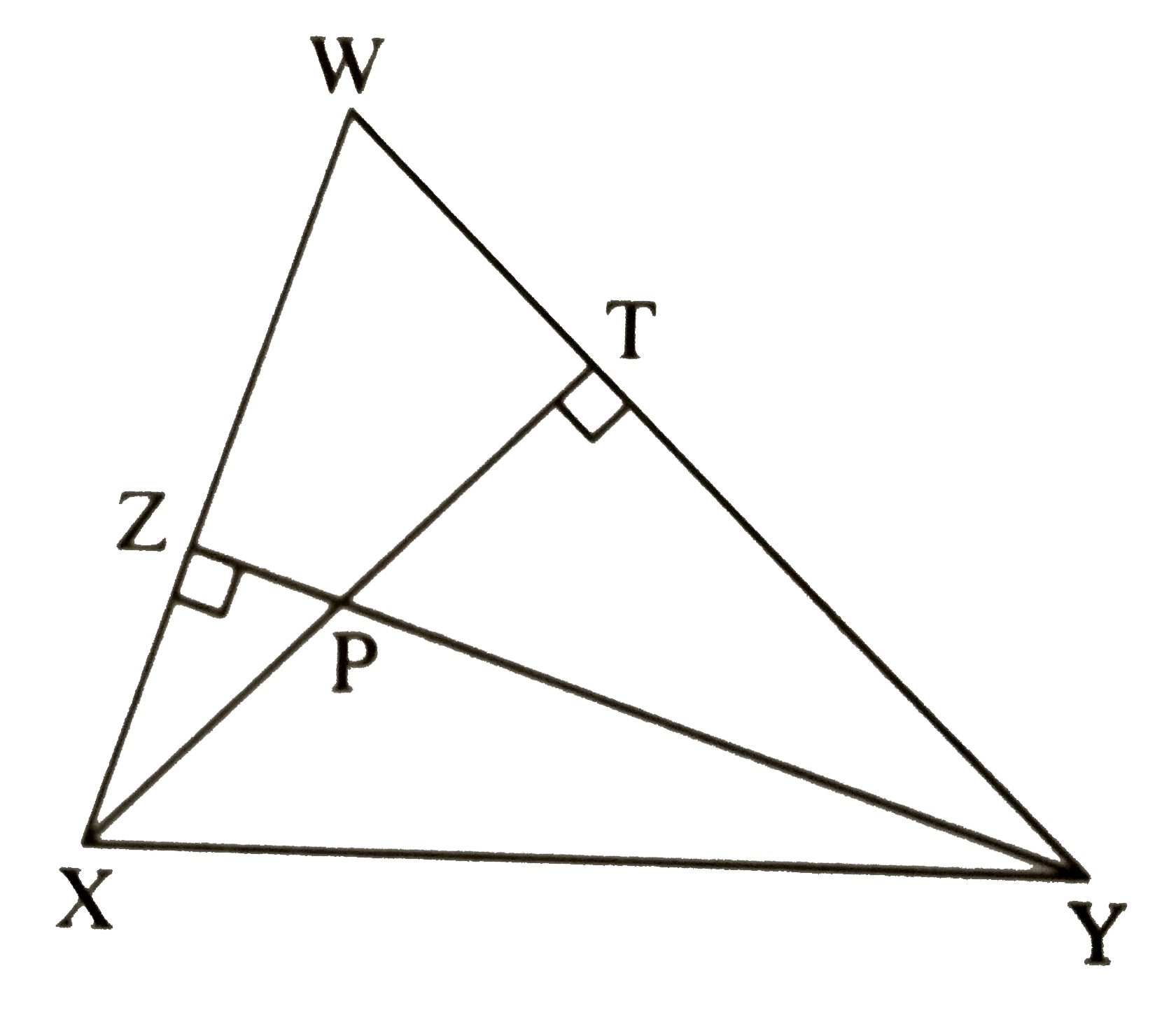
by converse of cyclic qyadrilateral theorem, is cyclic.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.56videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PROBLEM SET 350videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.33videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
In figure, altitudes YZ and XT of △WXY intersect at P. Prove that
Points X,Z,T,Y are concyclic.
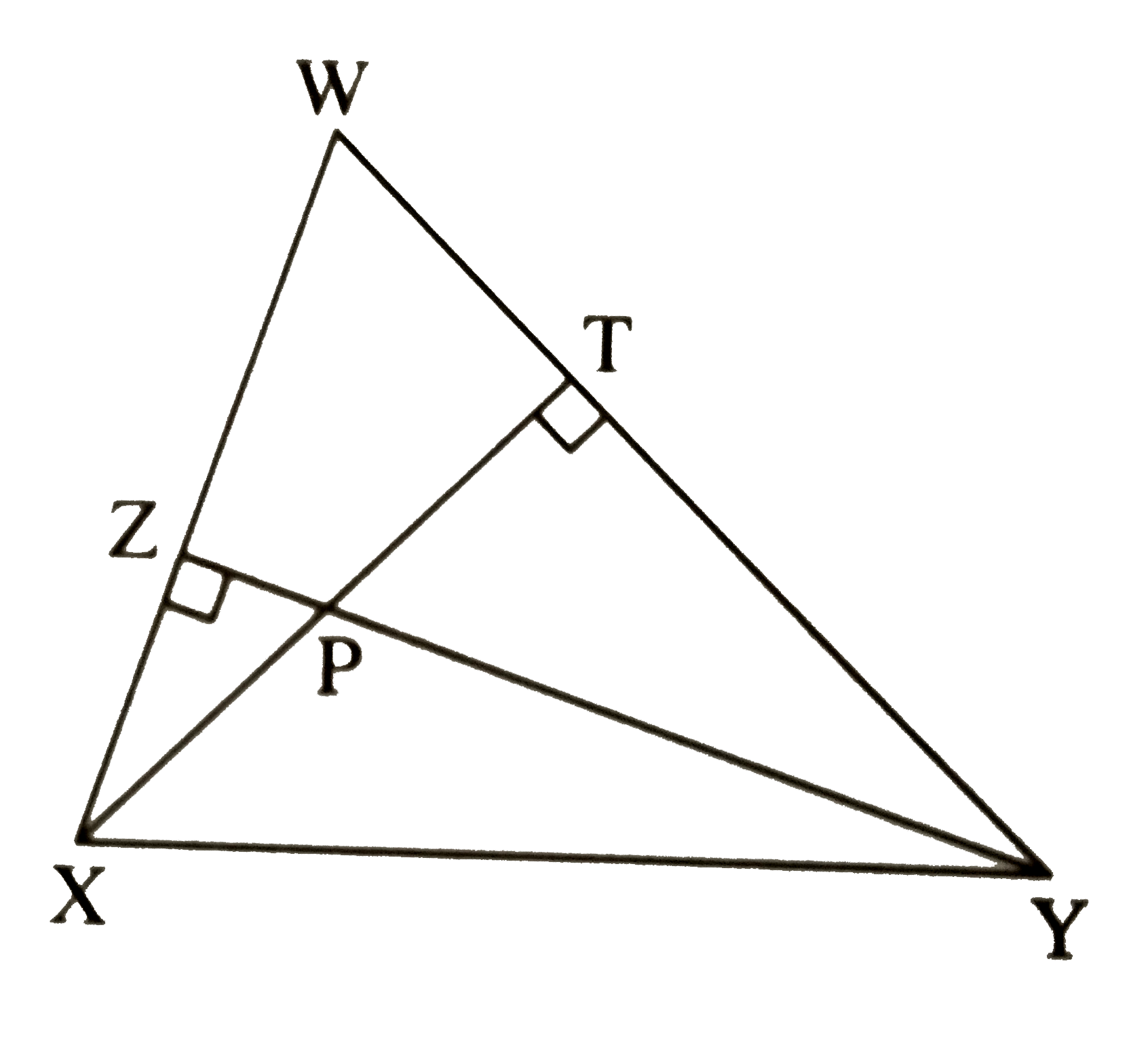 View Solution
View SolutionIn figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If the altitudes of a triangle are in A.P,then the sides of the triangle are in
AA.P.BG.P.CH.P.Dnone of these
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral, so formed is cyclic.
View SolutionIn the figure , altitudes AD and CE of ΔABC intersect each other at the point P . Show that :
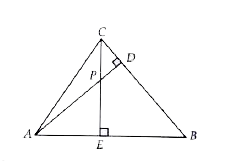
ΔAEP~ΔCDPView SolutionA circle intersects the side AD of a parallelogram ABCD at P and BC produced at Q. Prove that square PDQC is cyclic .
View SolutionIn the figure, if ∠ADC=∠CBP then prove that □ABCD is cyclic.
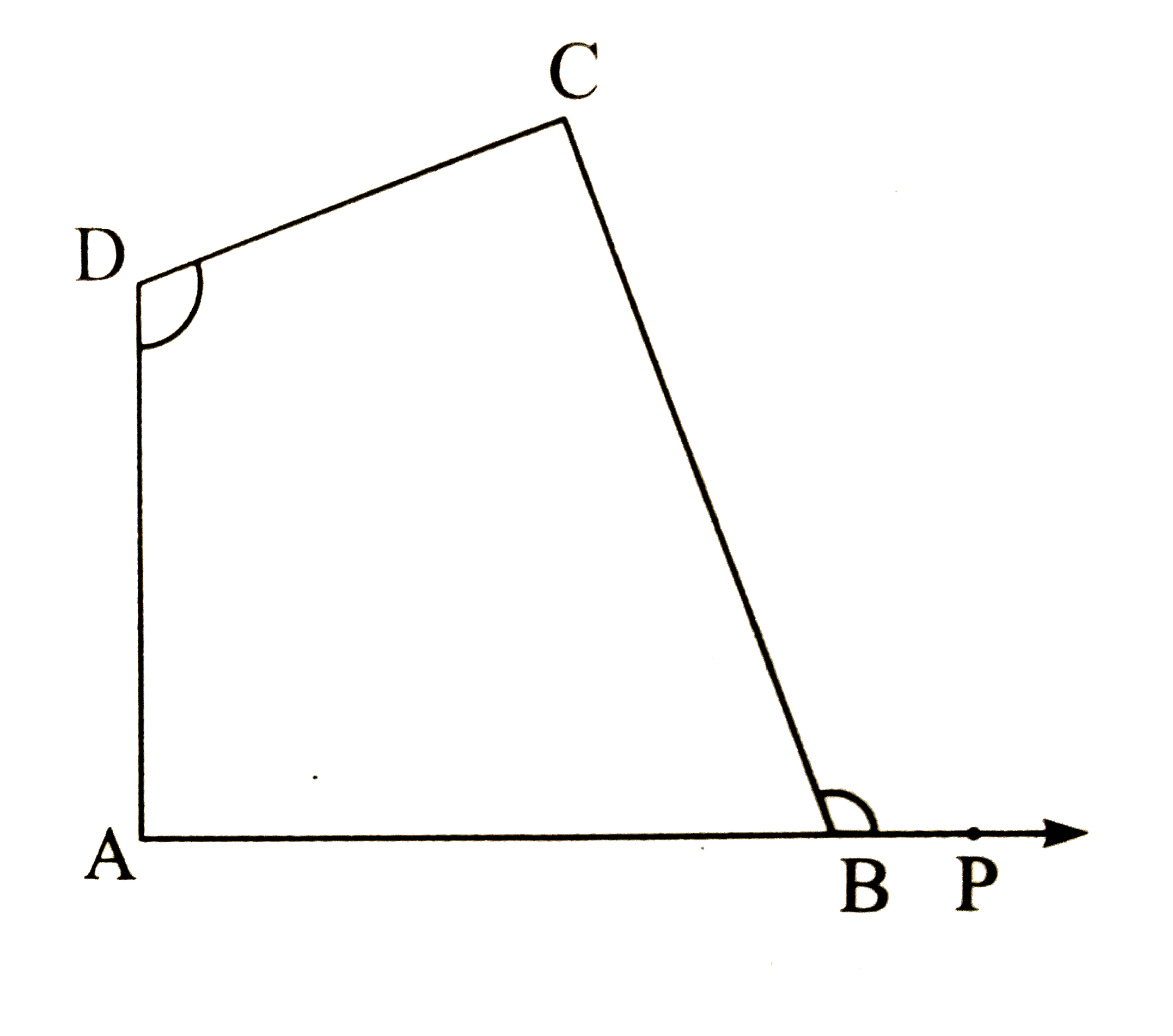 View Solution
View SolutionIn the given figure, points S,T and U are the midpoints of sides PQ,QR and PR respectively. IF PV⊥QR, then prove that □ SVTU is a cyclic quadrilateral.
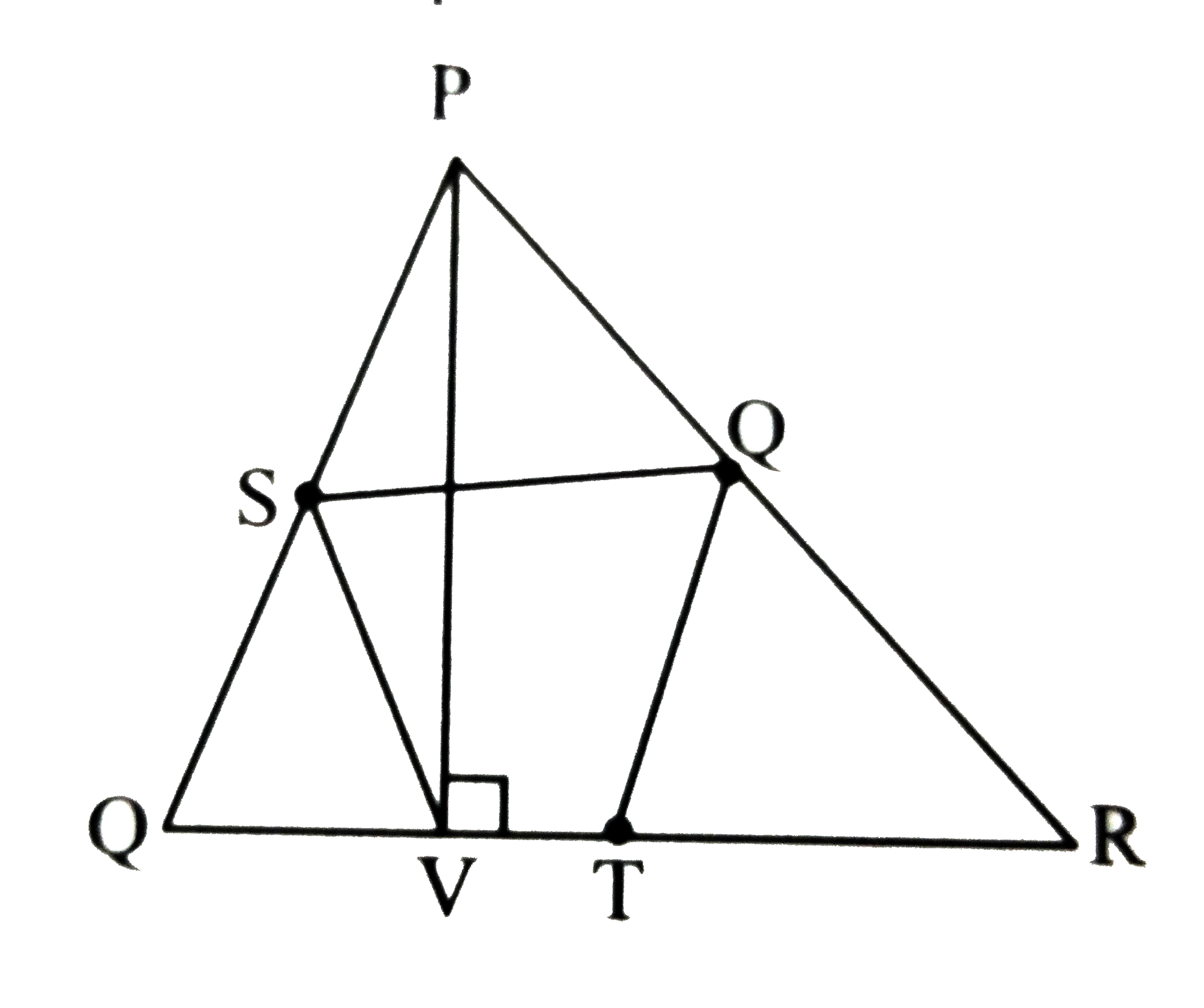 View Solution
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : ΔAPC~ΔDPB
 View Solution
View SolutionIn ΔABC, P,Q and R are midpoints of sides AB,AC and BC respectively. Seg AS⊥BC and PQ || BR side BC. Prove that □ PQRS is a cyclic quadrilateral.
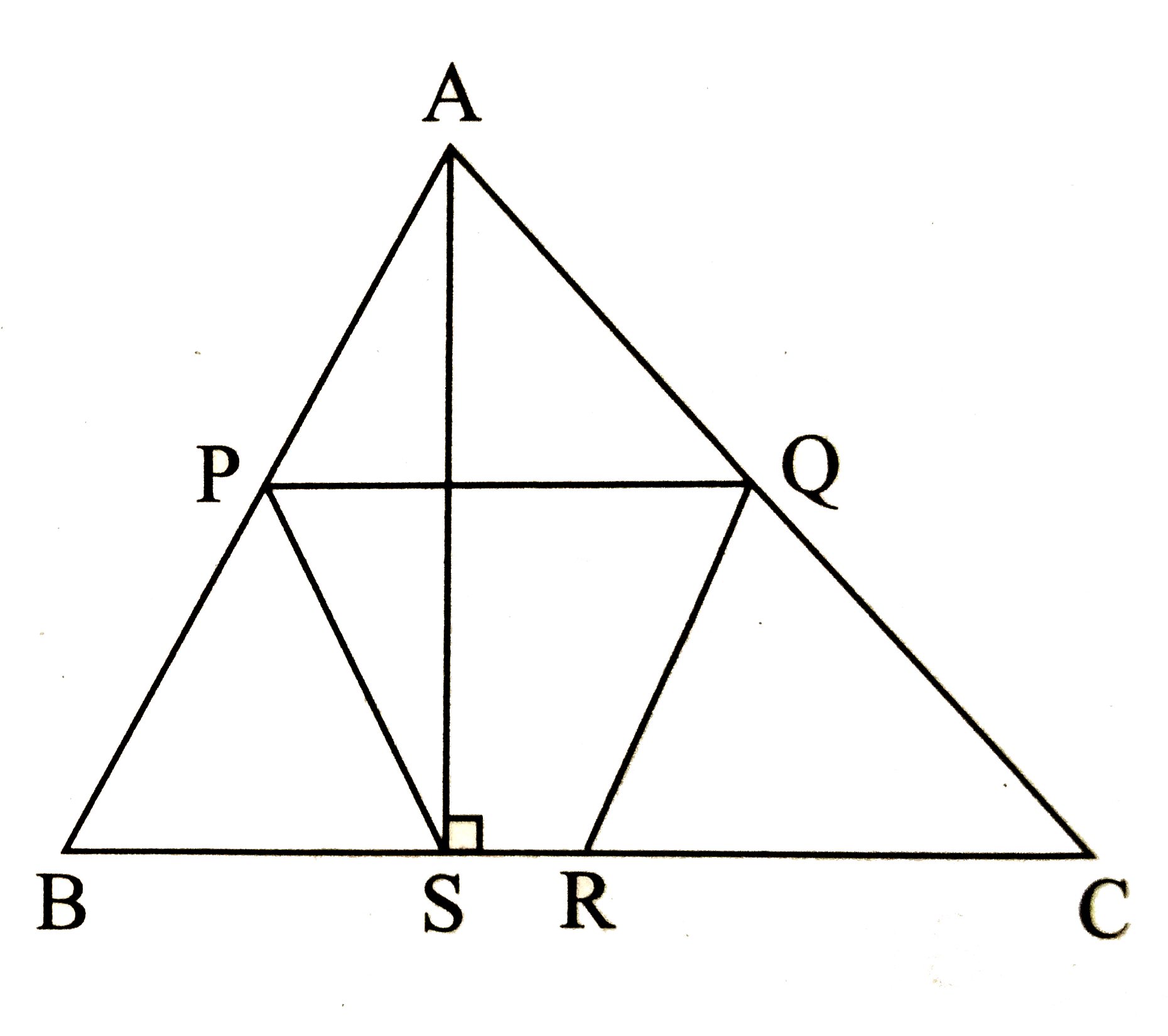 View Solution
View Solution

