Question

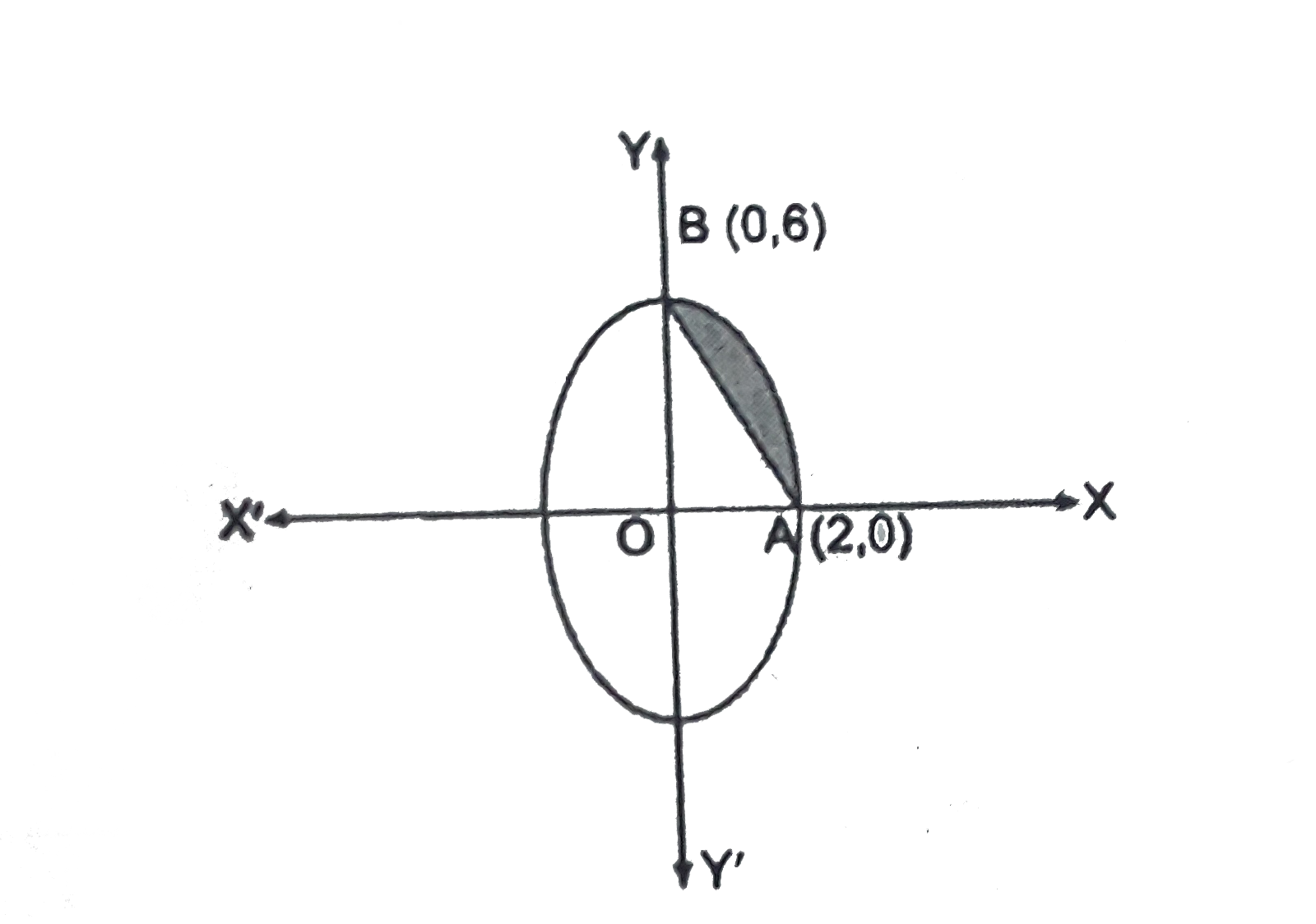
In Figure, AOBA is the part of the ellipse $9x^2+y^2=36$in the first quadrant such that $OA=2andOB=6$. Find the area between the arc AB and the chord AB.

Explanation

To find the area between the arc AB and the chord AB of the ellipse given by the equation $$9x^2+y^2=36$$ in the first quadrant, we will follow these steps:

Step 1: Rewrite the equation of the ellipse
We start with the equation of the ellipse:
\( 9x^2 + y^2 = 36 \)
To rewrite this in standard form, we divide both sides by 36:
\( \frac{x^2}{4} + \frac{y^2}{36} = 1 \)
This tells us that the semi-major axis \(a = 6\) (along the y-axis) and the semi-minor axis \(b = 2\) (along the x-axis).

Step 2: Identify points A and B
From the problem, we know:
- Point \(O\) is at the origin \((0, 0)\).
- Point \(A\) is at \((2, 0)\) since \(OA = 2\).
- Point \(B\) is at \((0, 6)\) since \(OB = 6\).

Step 3: Find the area of the sector OAB
To find the area between the arc AB and the chord AB, we first need to find the area of the sector OAB. The area under the curve from \(O\) to \(A\) can be calculated using integration.

The equation for \(y\) in terms of \(x\) is:
\( y = \sqrt{36 - 9x^2} \)

Step 4: Calculate the area under the curve from \(O\) to \(A\)
We calculate the area \(A_{OACB}\) under the curve from \(x = 0\) to \(x = 2\):
\( A_{OACB} = \int_{0}^{2} \sqrt{36 - 9x^2} \, dx \)

To solve this integral, we can use the substitution \(x = \frac{2}{3} \sin \theta\):
\( dx = \frac{2}{3} \cos \theta \, d\theta \)
The limits change as follows:
- When \(x = 0\), \(\theta = 0\)
- When \(x = 2\), \(\theta = \frac{\pi}{2}\)

The integral becomes:
\( A_{OACB} = \int_{0}^{\frac{\pi}{2}} \sqrt{36 - 9\left(\frac{2}{3} \sin \theta\right)^2} \cdot \frac{2}{3} \cos \theta \, d\theta \)
Simplifying inside the square root:
\( = \int_{0}^{\frac{\pi}{2}} \sqrt{36 - 4\sin^2 \theta} \cdot \frac{2}{3} \cos \theta \, d\theta \)
\( = \int_{0}^{\frac{\pi}{2}} \sqrt{36(1 - \frac{1}{9}\sin^2 \theta)} \cdot \frac{2}{3} \cos \theta \, d\theta \)
\( = 6 \cdot \frac{2}{3} \int_{0}^{\frac{\pi}{2}} \sqrt{1 - \frac{1}{9}\sin^2 \theta} \cos \theta \, d\theta \)

Step 5: Calculate the area of triangle OAB
The area of triangle \(OAB\) can be calculated using the formula:
\( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times OA \times OB = \frac{1}{2} \times 2 \times 6 = 6 \)

Step 6: Find the required area
The area between the arc AB and the chord AB is given by:
\( \text{Required Area} = A_{OACB} - \text{Area of triangle OAB} \)

Final Calculation
After performing the integration and substituting the values, we find:
\( \text{Required Area} = 3\pi - 6 \)