In the adjoining, OABO is the region of the ellips $9 x^{2} + y^{2} = 36$ which lies in first quadrant. If $O A = 2, O B = 6,$ then find the area of the region bounded by chord AB and arc AB.

Video Solution

Text Solution

Verified by Experts

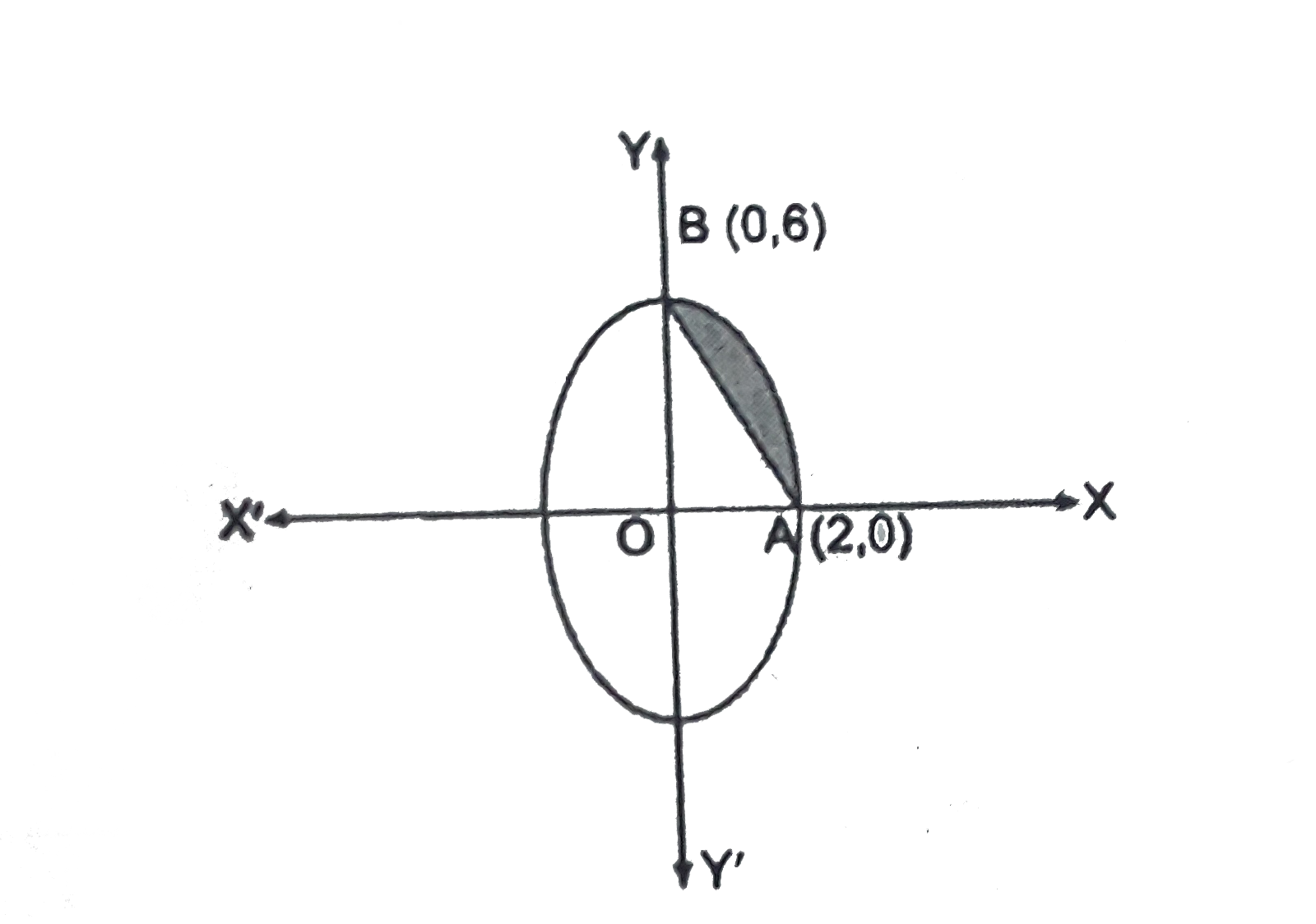
Equation of AB
$y - 0 = \frac{6 - 0}{0 - 2} (x - 2)$
$\Rightarrow y = - 3 x + 6$
Required area
$= \int_{0}^{2} 3 \sqrt{4 - x^{2}} d x - \int_{0}^{2} (- 3 x + 6) d x$
$= 3 {[\frac{x}{2} \sqrt{4 - x^{2}} + \frac{4}{2} {sin}^{- 1} \frac{x}{2}]}_{0}^{2} - {[\frac{- 3 x^{2}}{2} + 6 x]}_{0}^{2}$
$= 3 [(0 + 2 {sin}^{- 1} 1) - (0 + 0)] - [(- 6 + 12) - (0 + 0)]$
$= (3 π - 6) s q .$ units.

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF INTEGRALS-Miscellaneous Exercise

Home
Ask Doubt
Profile