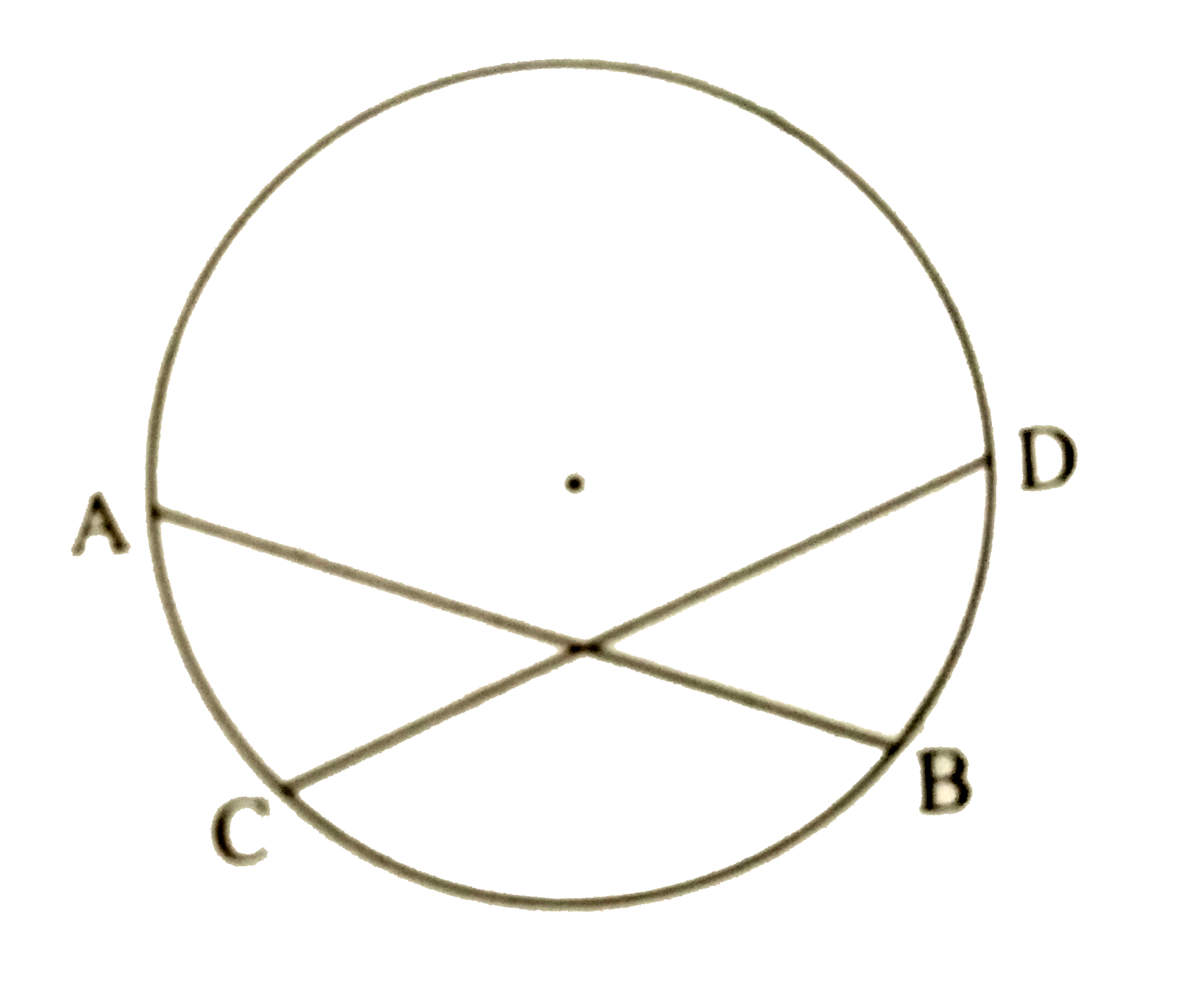
In figure, chord AB ≅ chord CD, Prove that, arc AC ≅ arc BD.
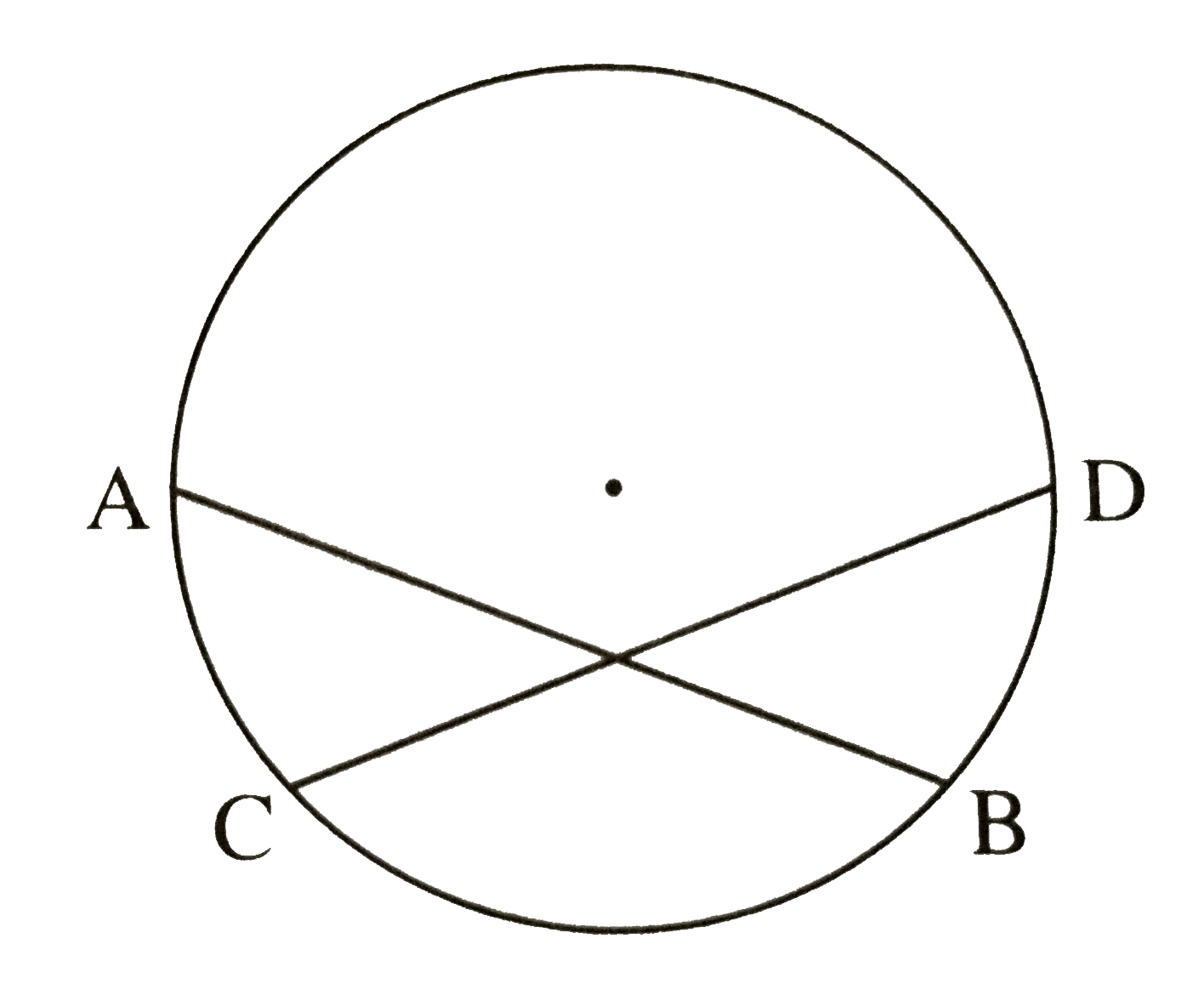
Chord AB ≅ chord CD ………( Given )
∴ArcACB≅arcCBD
………( Arcs corresponding to congruent chords )
∴m(arcACB)=m(arcCBD) ……(1)
But m(arcACB)=m(arcAC)+m(arcCB)……(2)
and m(arcCBD)=m(arcCB)+m(arcBD)……(3)
From (1),(2), and (3), we get,
m(arcAC)+m(arcCB)=m(arcCB)+m(arcBD)
∴m(arcAC)=m(arcBD)
∴arcAC≅arcBD.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.415videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.56videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.28videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
If AB≅CD then
AAB<CDBAB+CD=0CAB=CDDAB>CD
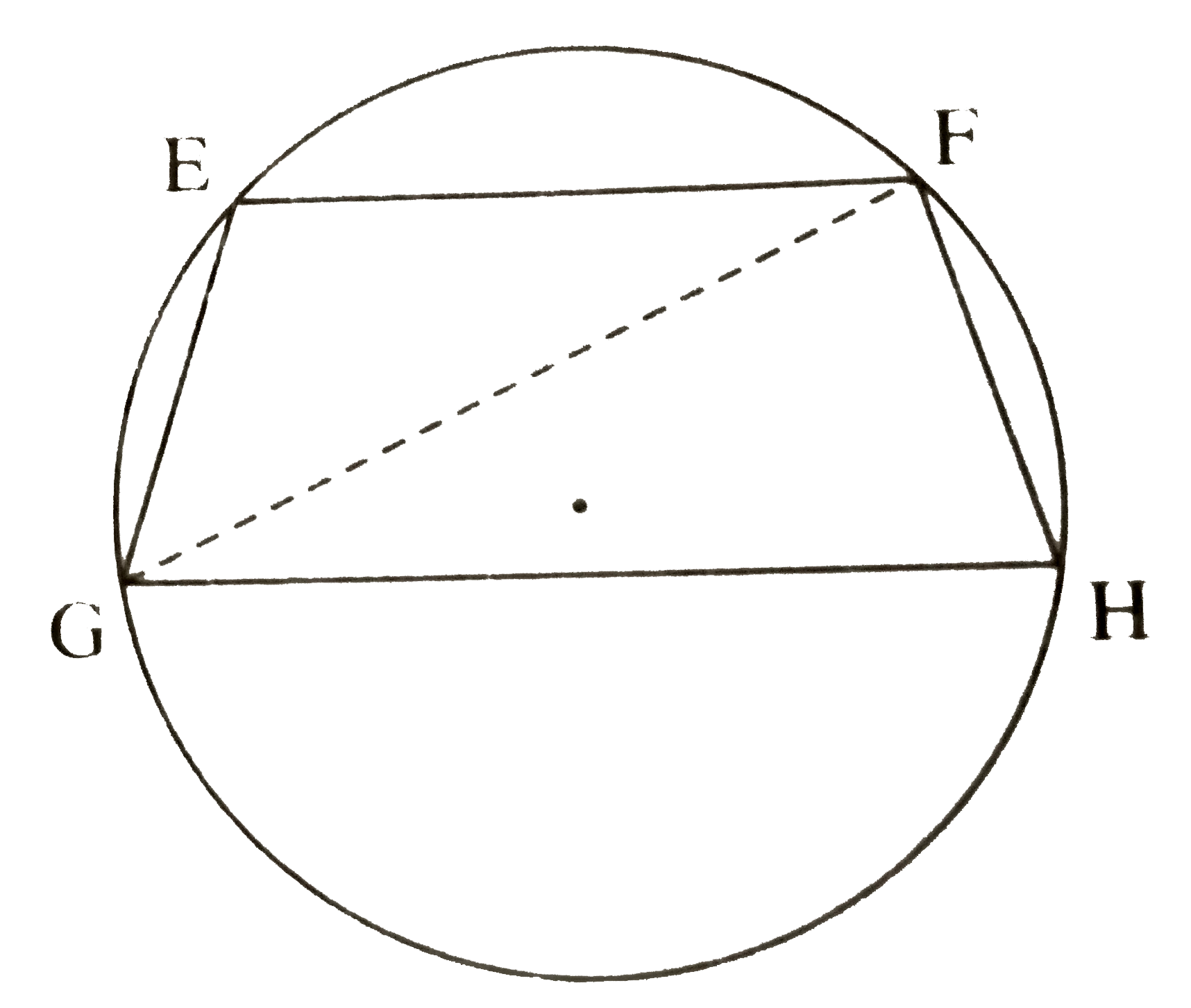
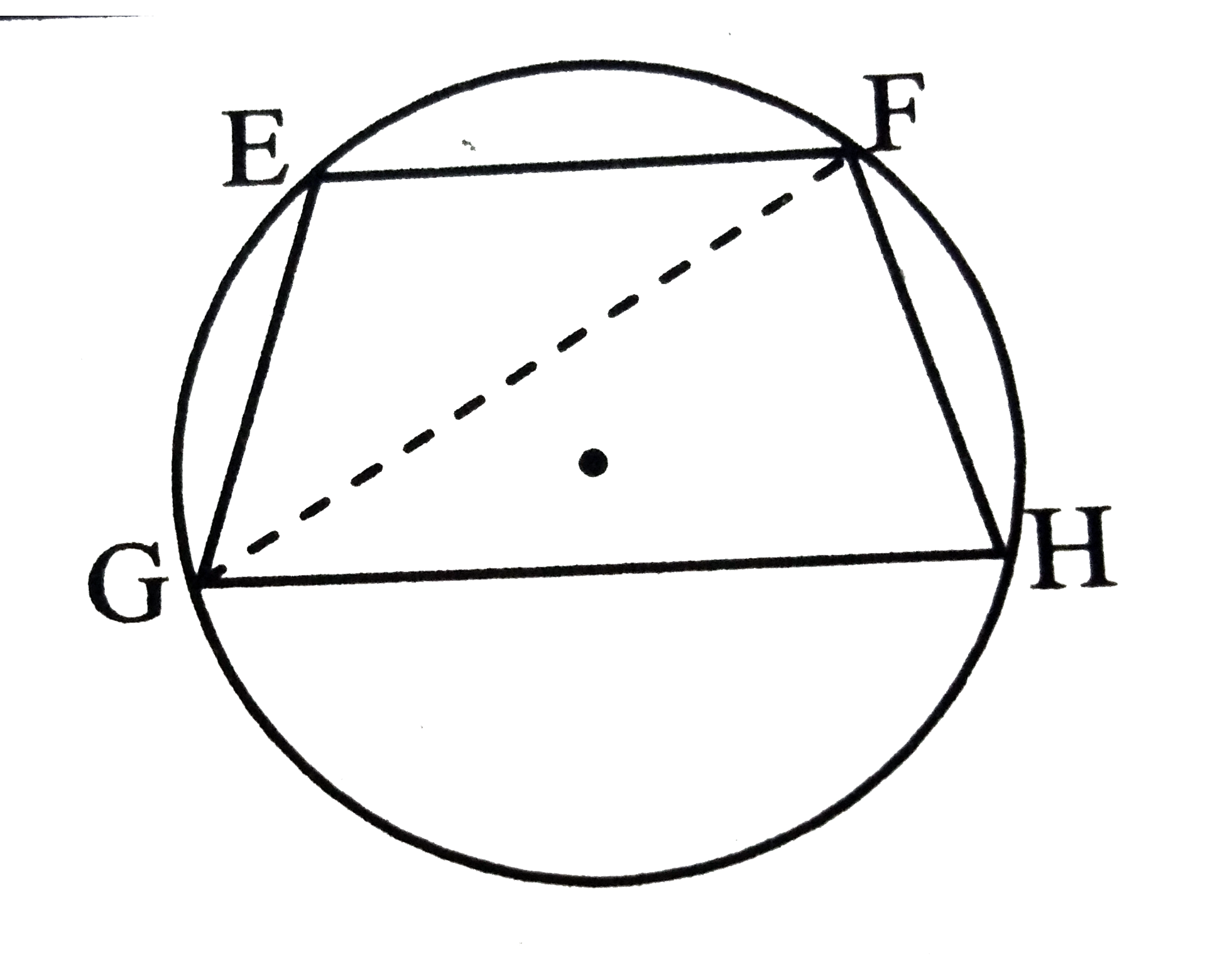
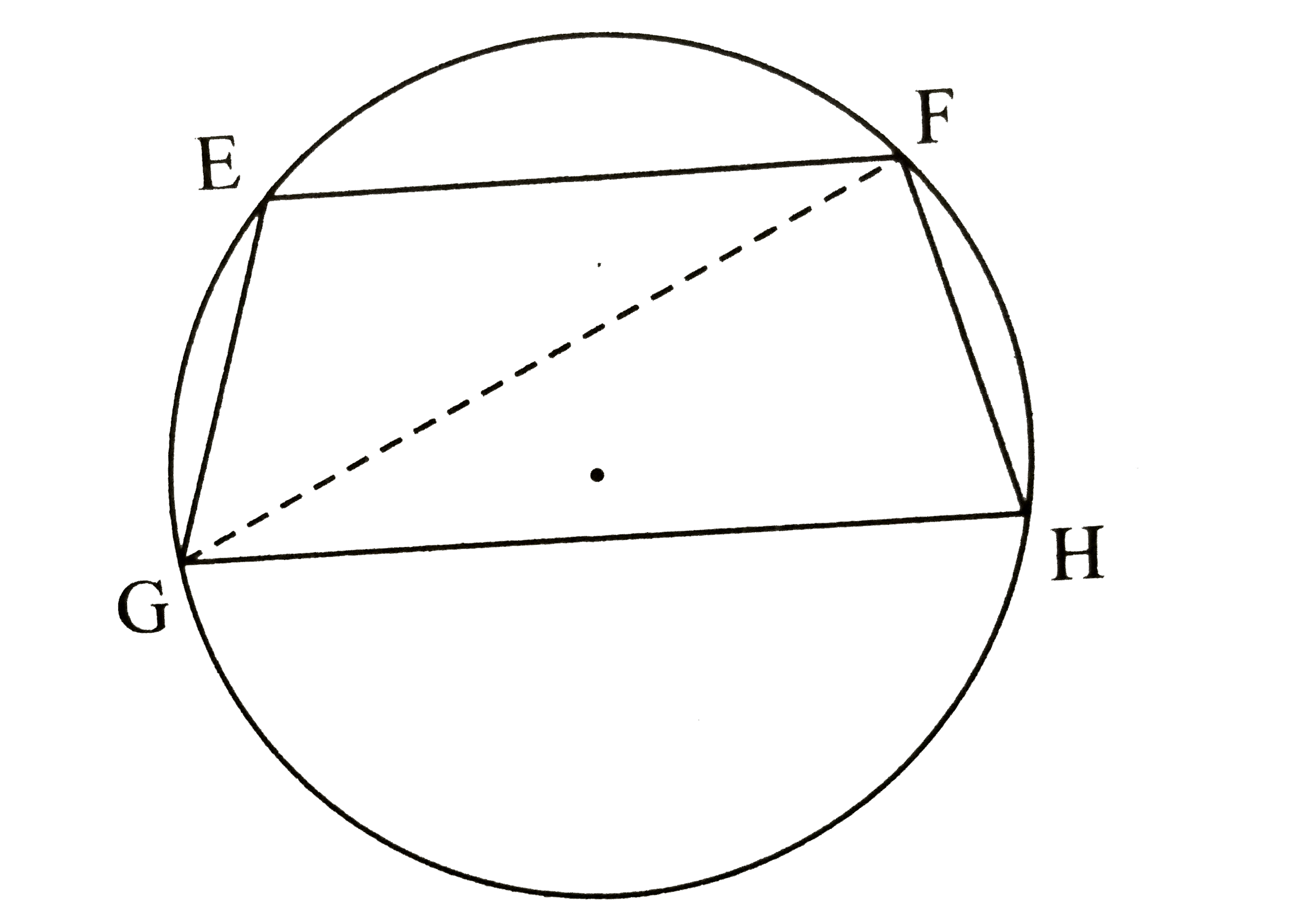
In the adjoining figure ,chord EF ∣∣ chord GH. Prove that, chord EG≅chord FH. Fill in the blanks and write the proof.
 View Solution
View SolutionIn the figure, chord EF∣∣ chord GH.
Prove that ,
chord EG ≅ chord FH .
Fill in the blanks and write the proof .
Proof : Draw seg GF.
∠EFG=∠FGH ….( □) …..(1)
∠EFG=□ …(Inscribed angle theorem ) ...(2)
∠FGH=□ ....(Inscribed angle theorem ) ...(3) ∴ m ( arc EG ) =□ ....[From (1), (2) and (3) ]
∴ Chord EG ≅ Chord FGH ....(Corresponding chords of congruent arcs )
 View Solution
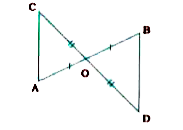
View SolutionIn the given figure AB and CD bisect each other at O. Prove that AC = BD.
 View Solution
View SolutionIf the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc PXA≅arc PYB.
 View Solution
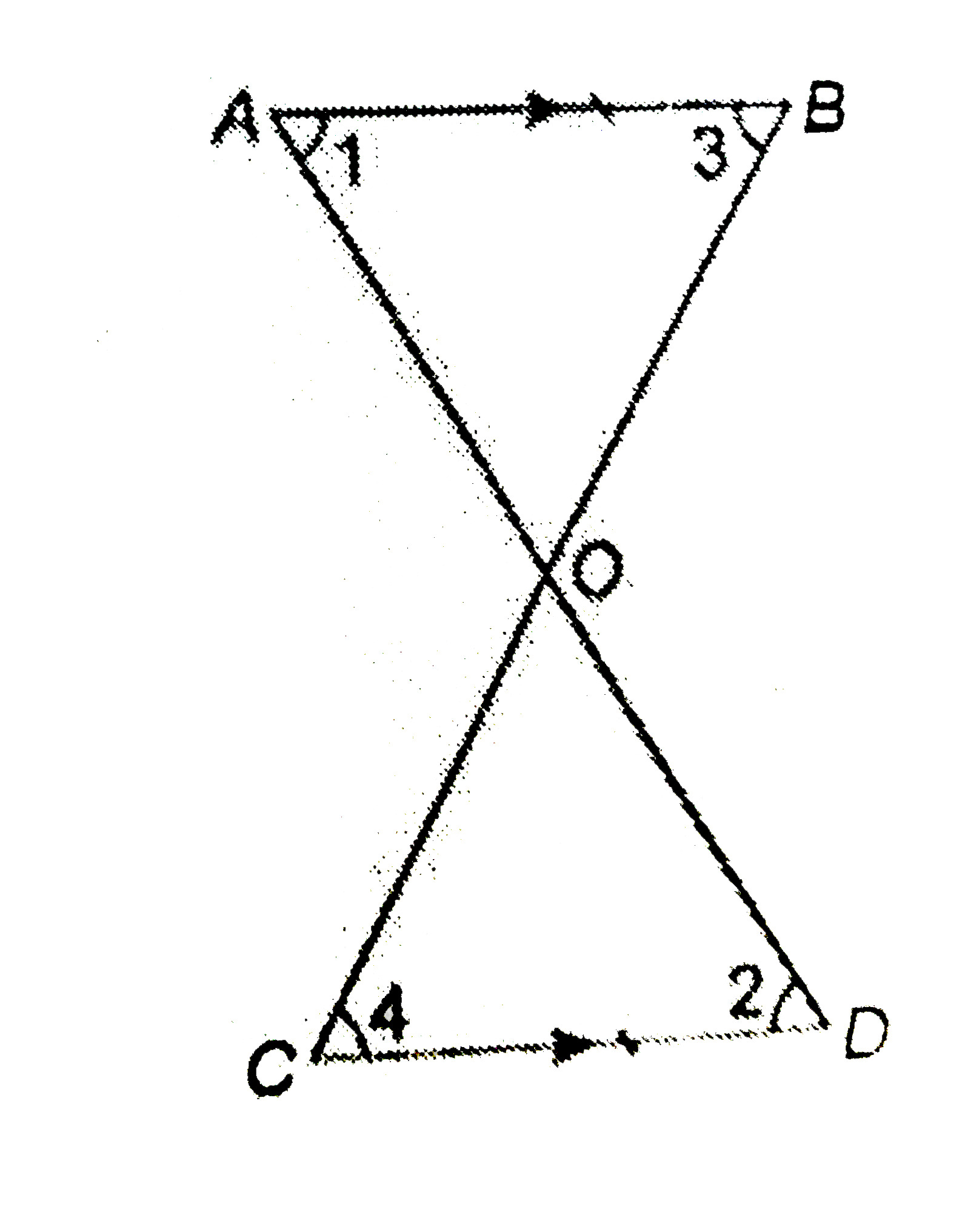
View SolutionIn the adjoining figure, AB = CD and AB||CD prove that
(i) ΔAOB≅ΔDOC
(ii) AD and BC bisect each other at the point O.
 View Solution
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : ΔAPC~ΔDPB
 View Solution
View SolutionIn the figure, two chords AB and CD intersect each other at the point P.
Prove that : AP. PB = CP. DP
 View Solution
View Solution