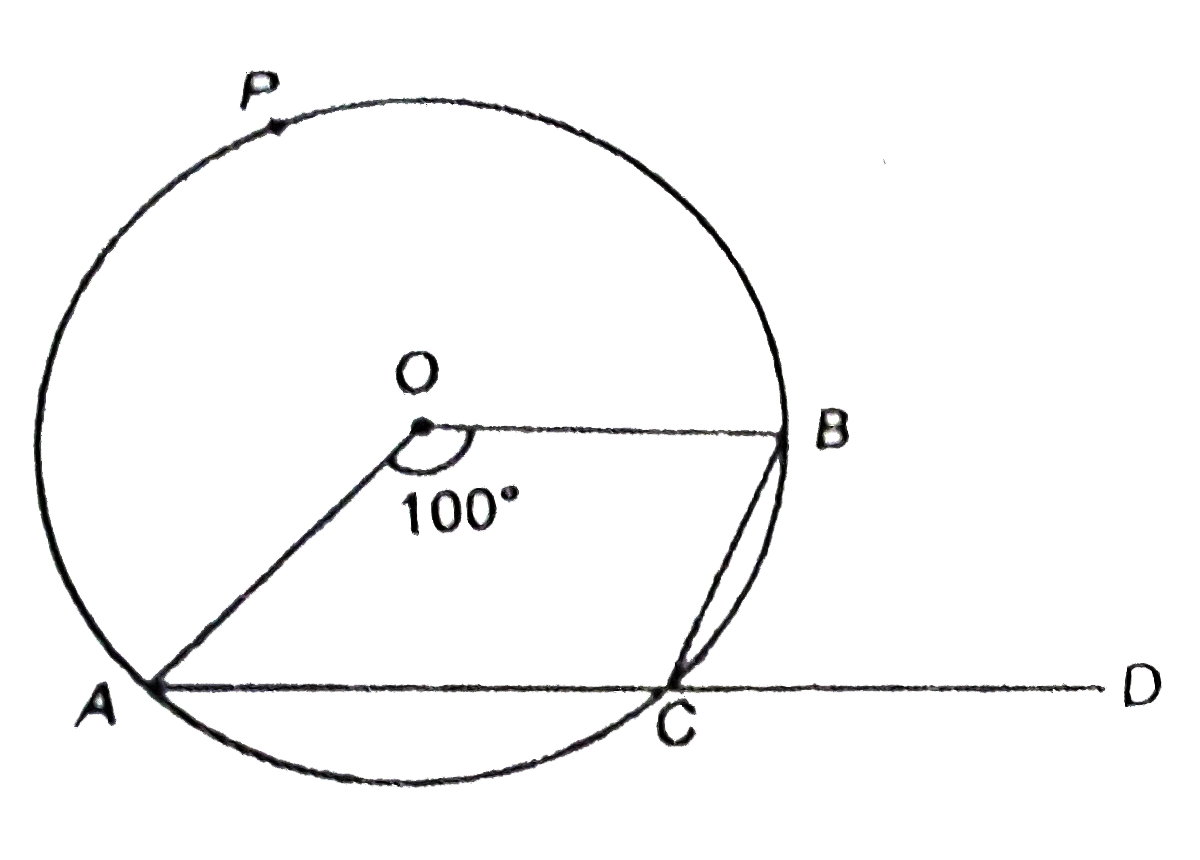
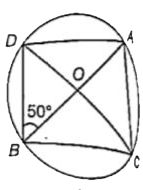
In figure, O is the centre of the circle ∠BCO=30∘ . Find X and Y.
Video Solution
Text Solution
Given, O is the centre of the circle and ∠BCO=30∘. In the given figure join OB and AC.
In ΔBOC,
CO=BO [both are the radius of circle]
∴∠OBC=∠OCB=30∘
[angles opposite to equal sides are equal]
∴∠BOC=180∘−(∠OBC+∠OCE)
[ by angle sum property of a triangle]
=180∘−(30∘+30∘)=120∘
∠BOC=2∠BAC
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
∴∠BAC=120∘2=60∘
Also, ∠BAE=∠CAE=30∘ [[AE is an angle bisector of angle A]
⇒∠BAE=x=30∘
In ΔABE,∠BAE+∠EBA+anlg≤AEB=180∘
[by angle sum property of a triangle]
⇒30∘+∠EBA+90∘=180∘
∴∠EBA=180∘−(90∘+30∘)=180∘−120∘=60∘
Now, ∠EBA=60∘
⇒∠ABD+y=60∘
⇒12×∠AOD+y=60∘
[in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle]
⇒90∘2+y=60∘[∵∠AOD=90∘, given]
⇒45∘+y=60∘
⇒y=60∘−45∘
∴y=15∘
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In Fig, O is the center of the circle. Find the angle of △ABC.
 A130∘B150∘C135∘Dcan't be determined
A130∘B150∘C135∘Dcan't be determinedIn the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.
 A=60∘B=45∘C=30∘D=50∘
A=60∘B=45∘C=30∘D=50∘In the given figure, O is the centre of the circle. If ∠BAO=30∘ and ∠BCO=50∘ , then ∠AOC is equal to:
 A60∘B80∘C40∘D160∘
A60∘B80∘C40∘D160∘
In Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
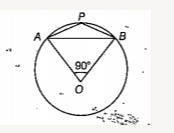
View SolutionIn the given figure, O is the centre of the circle∠AOB=90∘ Find m∠APB
View SolutionIn the adjoining figure, O is the centre of the circle and D ∠OBD=50∘. Find the ∠BAD :
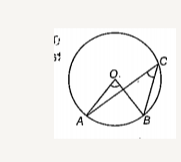
View SolutionIn the given figure, O is the centre of the circle and ∠ACB=25∘ Find ∠AOB
View Solution