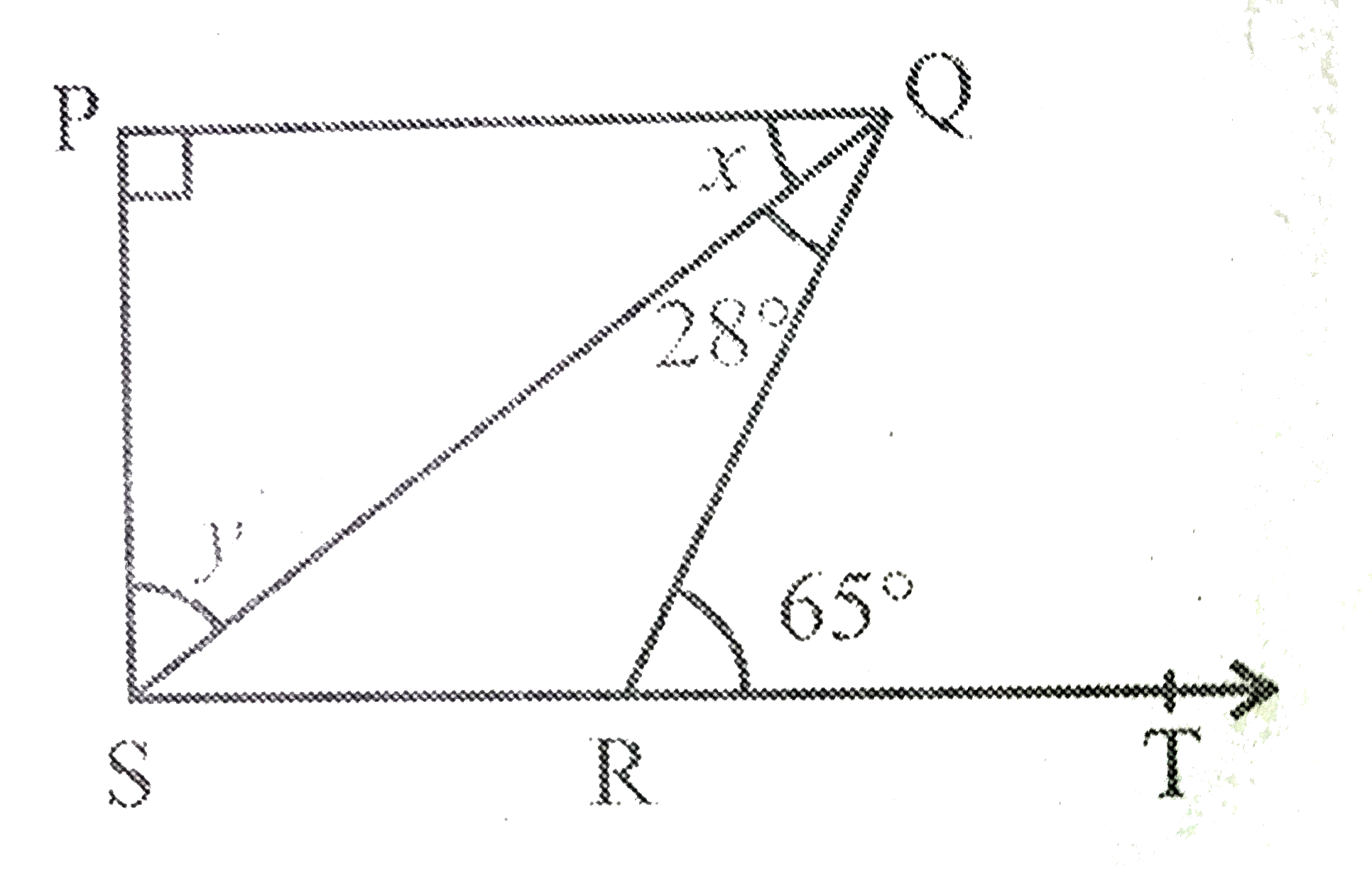
Given ∠POR=3xand∠QOR=2x+10, find the value of x for which POQ will be a line
Since QOR, POP are linear pairs
∠OOR+∠POR=180∘
2x+10+3x=180∘[:∠QOR=2x+10,POR=3x]
5x+10=180∘
⇒5x=180∘−10
⇒5x=170∘
⇒x=34∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If x#y=x+yxy, then the value of P#(q#r) for every p, q, in N :
Aa. pq+qr+r2p(q+q+r)Bb. pqr+q+rp(q+r)Cc. p(qr+q+r)pqrDd. None of these
In a triangle PQR , let ∠PQR=30o and the sides PQ and QR have lengths 10√3 and 10, respectively. Then, which of the following statement(s) is (are) TRUE? ∠QPR=45o (b) The area of the triangle PQR is 25√3 and ∠QRP=120o (c) The radius of the incircle of the triangle PQR is 10√3−15 (d) The area of the circumcircle of the triangle PQR is 100 π
View SolutionConsider two points P and Q with position vectors −−→OP=3→a−2→b and −−→OQ=→a+→bFind the position vector of a point R which divides the line joining P and Q in the ratio 2:1,
(i) internally, and (ii) externally.View SolutionThe line x+y=p meets the x- and y-axes at AandB , respectively. A triangle APQ is inscribed in triangle OAB,O being the origin, with right angle at Q.P and Q lie, respectively, on OBandAB . If the area of triangle APQ is 38th of the are of triangle OAB, the AQBQ is equal to (a)2(b) 23 (c) 13 (d)3
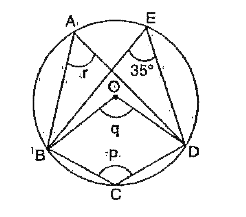
View SolutionO is the centre of the circle. Find the values of p, q and r.
 View Solution
View SolutionIn Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that: PL=QM (ii) LO=OM
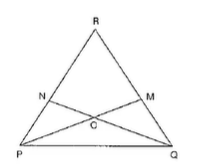
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
 View Solution
View SolutionP is a point on positive x-axis, Q is a point on the positive y-axis and 'O' is the origin. If the line passing through P and Q is tangent to the curve y=3−x2 then find the minimum area of the triangle OPQ , is 3 (b) 4 (c) 5 (c) 6
View Solution