In figure, ⌢AB≅⌢AC and O is the centre of the circle,Prove that OA is the perpendicualr bisector of BC.
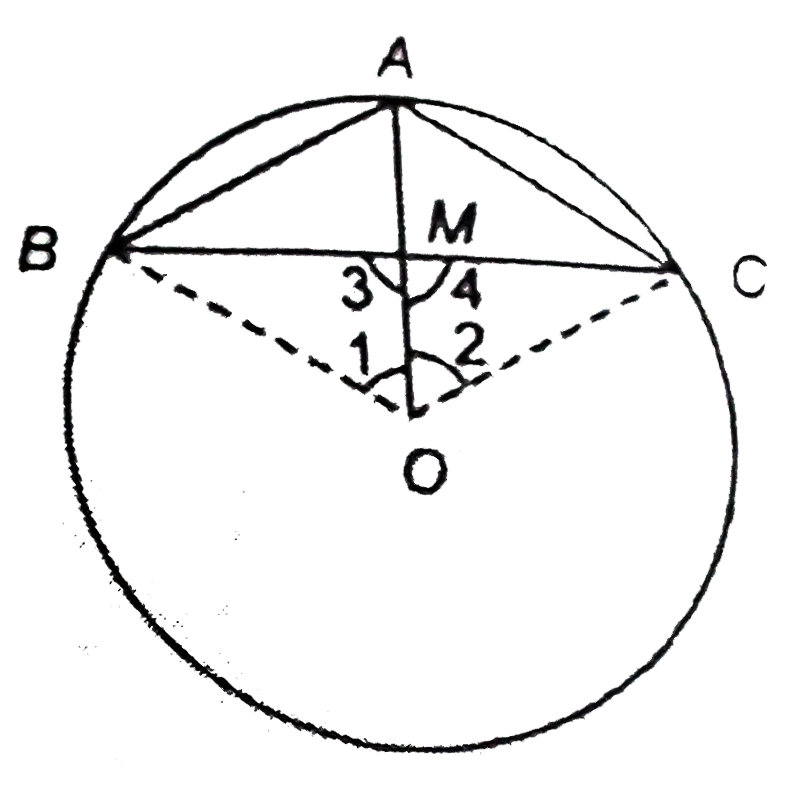
Since ⌢AB≅⌢AC (given)
⇒AB=AC (corresponding chords of congruent arcs are equal)
In ΔOAB and ΔOAC,
∵ ⎧⎪⎨⎪⎩AB=AC(just proved)OA=OA(common)OB=OC(each radii)
∴ΔOAB≅ΔOAC (by SSS congruency)
∴∠1=∠2 (c.p.c.t)
Now, in ΔOMB and ΔOMC,
∵ ⎧⎪⎨⎪⎩OB=AC(each radii)∠1=∠2(just proved)OM=OM(common)
∴ΔOMB≅ΔOMC (by S.A.S. congruency)
∴BM=MC (c.p.c.t) .......(1)
Also, ∠3=∠4 (c.p.c.t)
But ∠3+∠4=180∘ (L.P.A.)
⇒∠3=∠4=90∘ ......(2)
From (1) and (2) , we get
OM is the perpendicular bisector of BC.
⇒OA is the perpendicular bisector of BC.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Knowledge Check
AB and AC are tangents to the circle with centre O. Then x equals.
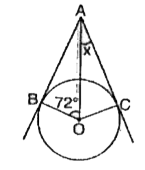 A22∘B18∘C20∘D36∘
A22∘B18∘C20∘D36∘
A, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
View SolutionIn the figure, O is the center of the circle and BO is the bisector of angle ABC show that AB=BC
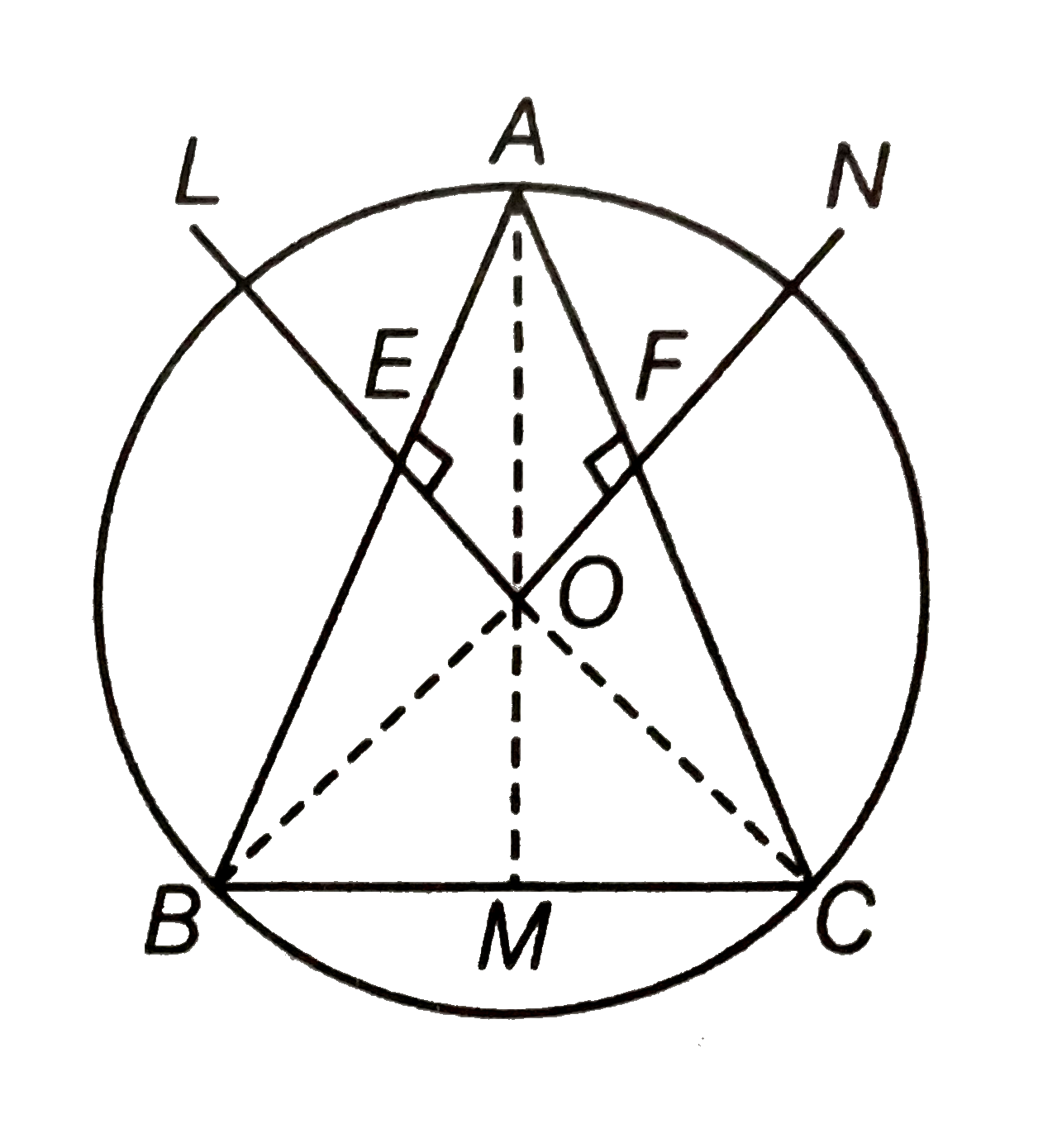
View SolutionFrom an external point P, two tangents PAandPB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
View Solution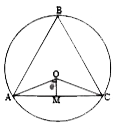
In the figure given above, O is the centre of the circle OA = 3 cm, AC = 3 cm and OM is perpendicular to AC. What is ∠ABC equal to ?
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.

View SolutionFrom a point P outside a circle with centre O, tangents PA and PB are drawn to the circle. Prove that OP is the right bisector of the line segment AB.
View Solution
