In Figure, is a transversal to lines and . Prove that
To prove that lines m and n are parallel given that angle 2=120∘ and angle 5=60∘, we can follow these steps:
Step 1: Identify the angles
We know from the problem statement that:
- ∠2=120∘
- ∠5=60∘
Step 2: Find angle 1
Since angles 2 and 1 form a linear pair (they are adjacent angles on a straight line), we can use the property that the sum of angles in a linear pair is 180∘.
∠1+∠2=180∘
Substituting the value of ∠2:
∠1+120∘=180∘
Now, solving for ∠1:
∠1=180∘−120∘=60∘
Step 3: Compare angles 1 and 5
Now we have:
∠1=60∘and∠5=60∘
Since ∠1 and ∠5 are corresponding angles (they are in the same relative position at each intersection of the transversal with the two lines), we can conclude:
∠1=∠5
Step 4: Conclude that lines m and n are parallel
According to the Corresponding Angles Postulate, if a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel.
Since ∠1=∠5, we can conclude that:
m∥n
Final Statement
Therefore, we have proved that lines m and n are parallel.
---
We know from the problem statement that:
- ∠2=120∘
- ∠5=60∘
Since angles 2 and 1 form a linear pair (they are adjacent angles on a straight line), we can use the property that the sum of angles in a linear pair is 180∘.
Now we have:
According to the Corresponding Angles Postulate, if a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel.
Therefore, we have proved that lines m and n are parallel.
Topper's Solved these Questions
Similar Questions
In Figure, if ∠2=1200and ∠5=600, show that m∣∣n.
View SolutionIn Fig. 54, if ∠2=1200 and ∠5=600, show that m∣∣n.
View SolutionIn Figure, transversal l intersects two lines m and n , ∠4=1100 and ∠7=650 . Is m∣∣n?
View SolutionIn the given figure, a transversal n cuts two lines l and m such that ∠2=650 and ∠8=650. Are the lines parallel?
View SolutionIn the given figure, a transversal n cuts two lines l and m if ∠1=700 and ∠7=800, is l ∣∣ m?
View SolutionIn Figure, if ∠3=610and ∠7=1180 . Is m∣∣n ?
View SolutionIn Fig., if l||m||n and ∠1=600, find ∠2.
View SolutionIn Figure, ∠1=600and ∠2=(23)rd of a right angle. Prove that l∣∣m
View SolutionIn Figure, AP and BQ are perpendiculars to the line segment AB and AP=BQ . Prove that O is the mid-point of line segment AB and PQ
View SolutionIn Figure, line n is a transversal to line landm . Identify the following Alternate and corresponding angles in
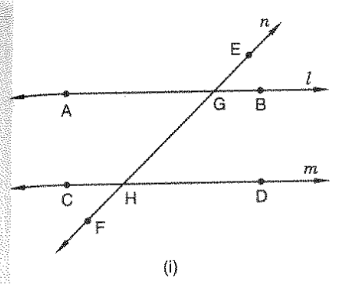
(ii) Angles alternate to ∠d a n d /_gand∠scorrespond∈g→∠s/_f\ a n d\ /_h∈figure<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/VI_RD_15_005_Q02.pngwh=80%mx-autosty≤=background:white;><br>(iii)Ang≤a<ernative→/_P Q R,∠correspond∈g→/_R Q Fand∠a<ernate→/_P Q E in Figure (iv) Pairs of interior and exterior angles on the same side of the transversal m in
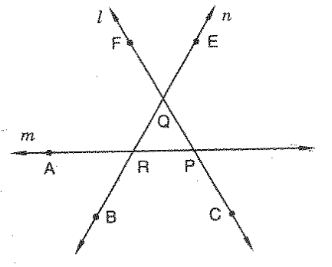 View Solution
View Solution

