In the given figure, a transversal n cuts two lines l and m if ∠1=700 and ∠7=800, is l ∣∣ m?
To determine whether lines l and m are parallel based on the given angles ∠1=70∘ and ∠7=80∘, we can follow these steps:
1. Identify the Angles: We are given that ∠1=70∘ and ∠7=80∘.
2. Determine Vertically Opposite Angles: Since ∠7 is given as 80∘, we know that ∠5, which is vertically opposite to ∠7, is also 80∘.
Thus, ∠5=∠7=80∘ (Vertically opposite angles)
3. Identify Corresponding Angles: Now, we look at ∠1 and ∠5. These angles are corresponding angles because they are on the same side of the transversal n and in corresponding positions relative to the two lines l and m.
4. Compare the Corresponding Angles: We compare the measures of ∠1 and ∠5:
∠1=70∘and∠5=80∘
Since 70∘≠80∘, we find that the corresponding angles are not equal.
5. Conclusion: According to the properties of parallel lines, if the corresponding angles are not equal, then the lines are not parallel. Therefore, we conclude that:
Lines l and m are not parallel.
Final Answer:
Lines l and m are not parallel.
Thus, ∠5=∠7=80∘ (Vertically opposite angles)
∠1=70∘and∠5=80∘
Since 70∘≠80∘, we find that the corresponding angles are not equal.
Lines l and m are not parallel.
Lines l and m are not parallel.
Topper's Solved these Questions
Similar Questions
In the given figure, a transversal n cuts two lines l and m such that ∠2=650 and ∠8=650. Are the lines parallel?
View SolutionIn Figure, transversal l intersects two lines m and n , ∠4=1100 and ∠7=650 . Is m∣∣n?
View SolutionIn Figure, p is a transversal to lines mandn and , ∠2=1200and ∠5=600 . Prove that m∣∣n
View SolutionIn the given figure, line l || m and a transversal n cuts them at P and Q respectively. If ∠1=750, find all other angles.
View SolutionIn the adjoining figure, transversal n cuts parallel lines l and m. If ∠5=65∘, find all other angles

View SolutionIn the given figure, AB||CD and a transversal PQ cuts them at L and M respectively. If ∠QMD=1000, find all other angles.
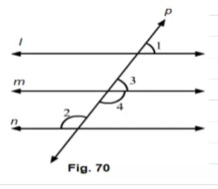
View SolutionIn Fig.70. if l||m||n and ∠1=60∘, find ∠2.
View SolutionIn the given figure, line l || m and n is a transversal. If ∠1=400, find all the angles and check that all corresponding angles and alternate angles are equal.
View SolutionIn Figure, line n is a transversal to line l and m. Identify the following:
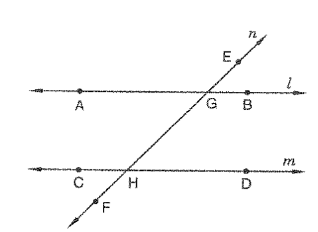
i) Alternate and corresponding angles in Figure
View SolutionIn the given figure, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively, If ∠CMQ=600 find all other angles in the figure.
View Solution
