In Figure PSSQ=PTTRand ∠PST=∠PRQ. Prove that PQR is an isosceles triangle.
Here, we are given,
PSSQ=PTTR
As, ST is dividing two sides of triangle in equal ratio, it will be parallel to third side.
So, ST∣∣QR
That means,
∠PST=∠PQR
We are given,
∠PST=∠PRQ
So, ∠PRQ=∠PQR
As two angles of triangle ΔPQR are equal, it is an isosceles triangle.
Similar Questions
In figure QRQS=QTPRand ∠1=∠2. Show that ΔPQS~ΔTQR.

View SolutionIn the given Fig. , if QTPR=QRQS and ∠1=∠2 . Prove that PQS~TQR . (FIGURE)
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.

View SolutionIf P + Q = R and P - Q = S, prove that R2+S2=2(P2+Q2)
View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.

View SolutionIn Fig. 4.90, if POS~ROQ , prove that PSQR . (FIGURE)
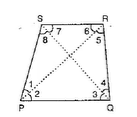
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
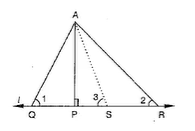
View SolutionIn Figure, AP ⊥l and PR>PQ . Show that AR>AQ Given: AP⊥l and PR>PQ To Prove: AR>AQ Construction: Mark a point S on PR such that PS=PQ. Join AS
View Solution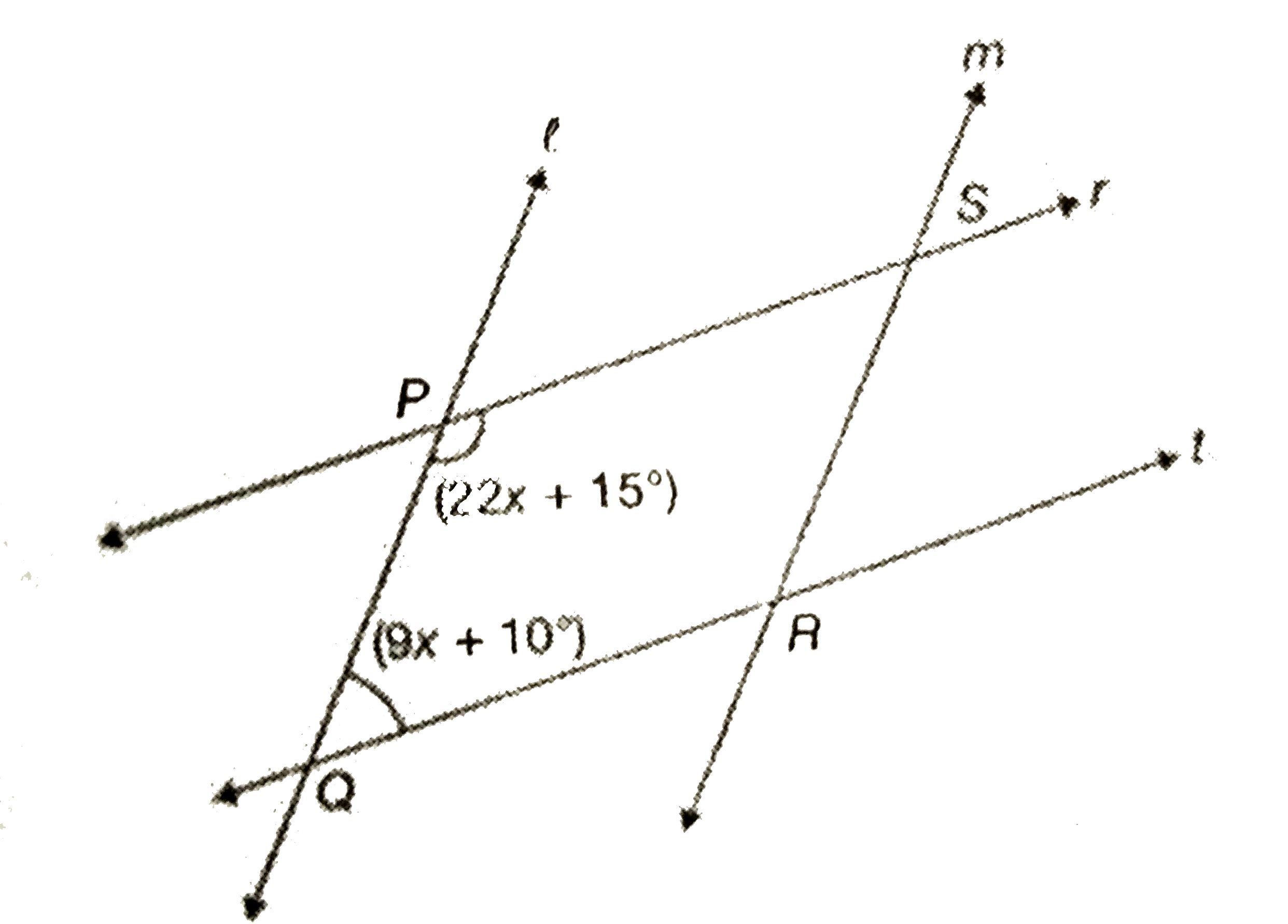
In the figure, l || mandr || t. They intersect at P, Q, R and S as shown in the figure. Find the angles of ∠SPQand∠PSR.
View Solution
