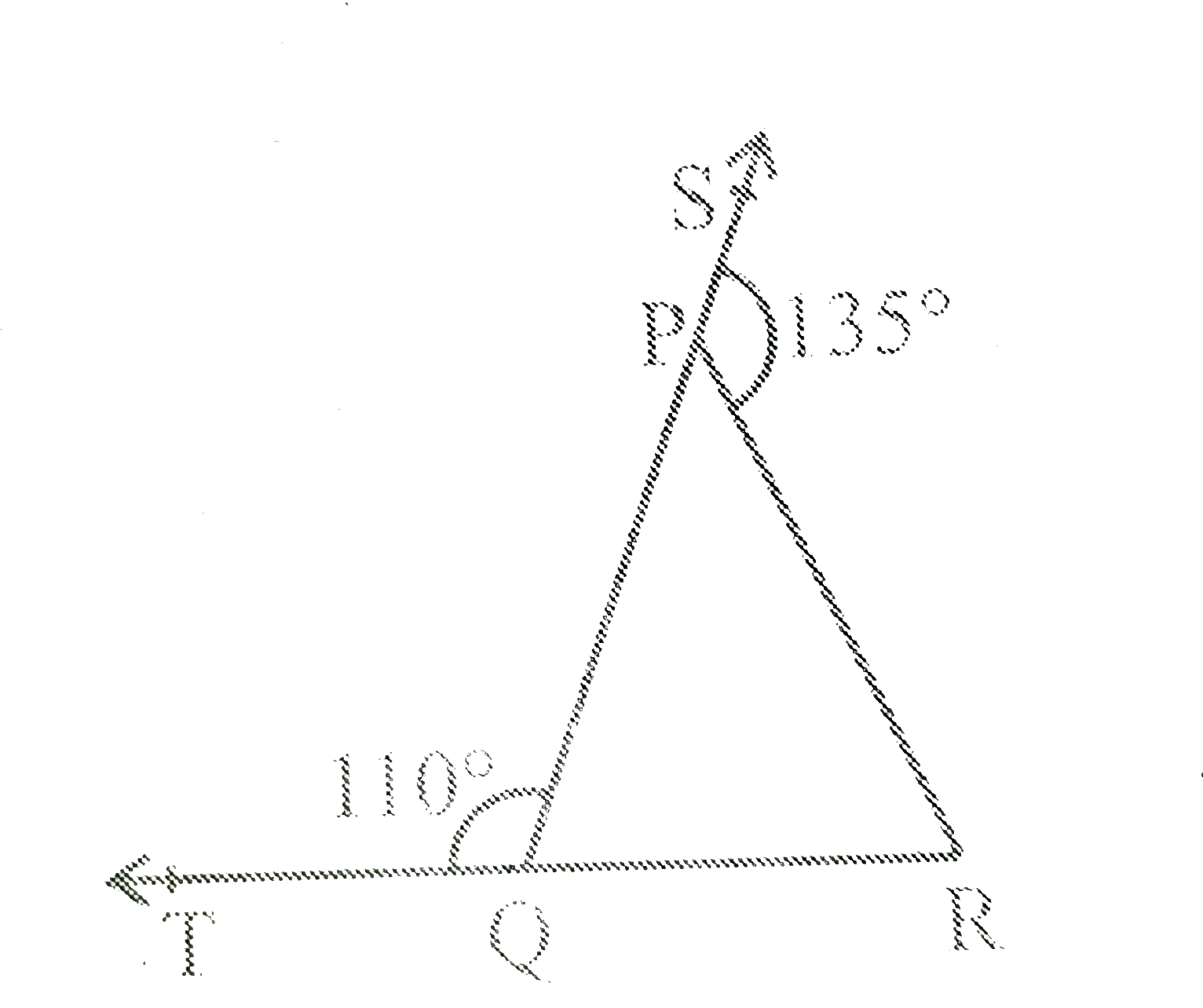
In Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.

Video Solution
Text Solution
Interior angles on the same side of the transversal:The pair of interior angles on the same side of the transversal are called consecutive interior angles or allied angles or co interior angles.
If a transversal intersects two Parallel Lines then each pair of interior angles on the same side of the transversal is supplementary.
If a transversal intersects two lines such that a pair of alternate interior angles is equal then the two lines are parallel.
SOLUTION :
Given :PQ || ST, ∠PQR=110∘ and ∠RST=130∘
Construction:A line XY parallel to PQ and ST is drawn.
∠PQR+∠QRX=180∘ (Angles on the same side of transversal.)
110∘+∠QRX=180∘
∠QRX=180∘−110∘
∠QRX=70∘
Also,∠RST+∠SRY=180∘ (Angles on the same side of transversal.)
130∘+∠SRY=180∘
∠SRY=50∘
Now, ∠QRX+∠SRY+∠QRS=180∘
70∘+50∘+∠QRS=180∘
∠QRS=60∘
Hence, ∠QRS=60∘
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES8videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.16videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - EXERCISE 4.42videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.121videos
NCERT THEOREMS
Similar Questions
Knowledge Check
- Question 1 - Select One
What should come next in the following letter series ?
P Q P Q R P Q R S P Q R S T P Q R S T L P Q R S T U V P Q R S TASBUCQDR
In Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
 View Solution
View SolutionIn Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.
 View Solution
View SolutionIn Fig. 4.90, if POS~ROQ , prove that PSQR . (FIGURE)
View SolutionIn Fig. 4.90, if PSQR , prove that POS~ROQ . (FIGURE)
View SolutionIn the given Fig. , if QTPR=QRQS and ∠1=∠2 . Prove that PQS~TQR . (FIGURE)
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
 View Solution
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.
 View Solution
View Solution