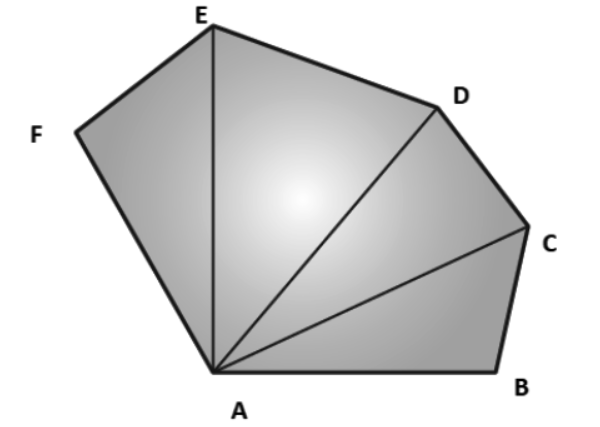
In five cornered fig. 18,AD,AC are joined. Find ∠EAB+∠ABC+∠BCD+∠CDE+∠DEA .
To solve the problem, we need to find the sum of the angles ∠EAB+∠ABC+∠BCD+∠CDE+∠DAE in the given five-cornered figure (pentagon).
1. Identify the Angles:
- Let’s label the angles in the pentagon ABCDE:
- ∠EAB=∠1+∠8+∠9
- ∠ABC=∠2
- ∠BCD=∠3+∠4
- ∠CDE=∠5+∠6
- ∠DAE=∠7
2. Use the Angle Sum Property of Triangles:
- In triangle ABC:
∠1+∠2+∠3=180∘(Equation 1)
- In triangle ACD:
∠9+∠5+∠4=180∘(Equation 2)
- In triangle ADE:
∠6+∠7+∠8=180∘(Equation 3)
3. Add the Equations:
- Now, we will add all three equations:
(∠1+∠2+∠3)+(∠9+∠5+∠4)+(∠6+∠7+∠8)=180∘+180∘+180∘
- This simplifies to:
∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9=540∘
4. Conclusion:
- Therefore, the sum of the angles ∠EAB+∠ABC+∠BCD+∠CDE+∠DAE is:
∠EAB+∠ABC+∠BCD+∠CDE+∠DAE=540∘
Final Answer:
The sum of the angles ∠EAB+∠ABC+∠BCD+∠CDE+∠DAE is 540∘.
- Let’s label the angles in the pentagon ABCDE:
- ∠EAB=∠1+∠8+∠9
- ∠ABC=∠2
- ∠BCD=∠3+∠4
- ∠CDE=∠5+∠6
- ∠DAE=∠7
- In triangle ABC:
∠1+∠2+∠3=180∘(Equation 1)
- In triangle ACD:
∠9+∠5+∠4=180∘(Equation 2)
- In triangle ADE:
∠6+∠7+∠8=180∘(Equation 3)
- Now, we will add all three equations:
(∠1+∠2+∠3)+(∠9+∠5+∠4)+(∠6+∠7+∠8)=180∘+180∘+180∘
- This simplifies to:
∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9=540∘
- Therefore, the sum of the angles ∠EAB+∠ABC+∠BCD+∠CDE+∠DAE is:
∠EAB+∠ABC+∠BCD+∠CDE+∠DAE=540∘
The sum of the angles ∠EAB+∠ABC+∠BCD+∠CDE+∠DAE is 540∘.
Topper's Solved these Questions
Similar Questions
In the six cornered figure, (fig.20), AC,AD and AE are joined. Find ∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠EFA.
View SolutionIn Figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC
View SolutionIn Figure, if △ABE≅△ACD , prove that △ADE~△ABC .
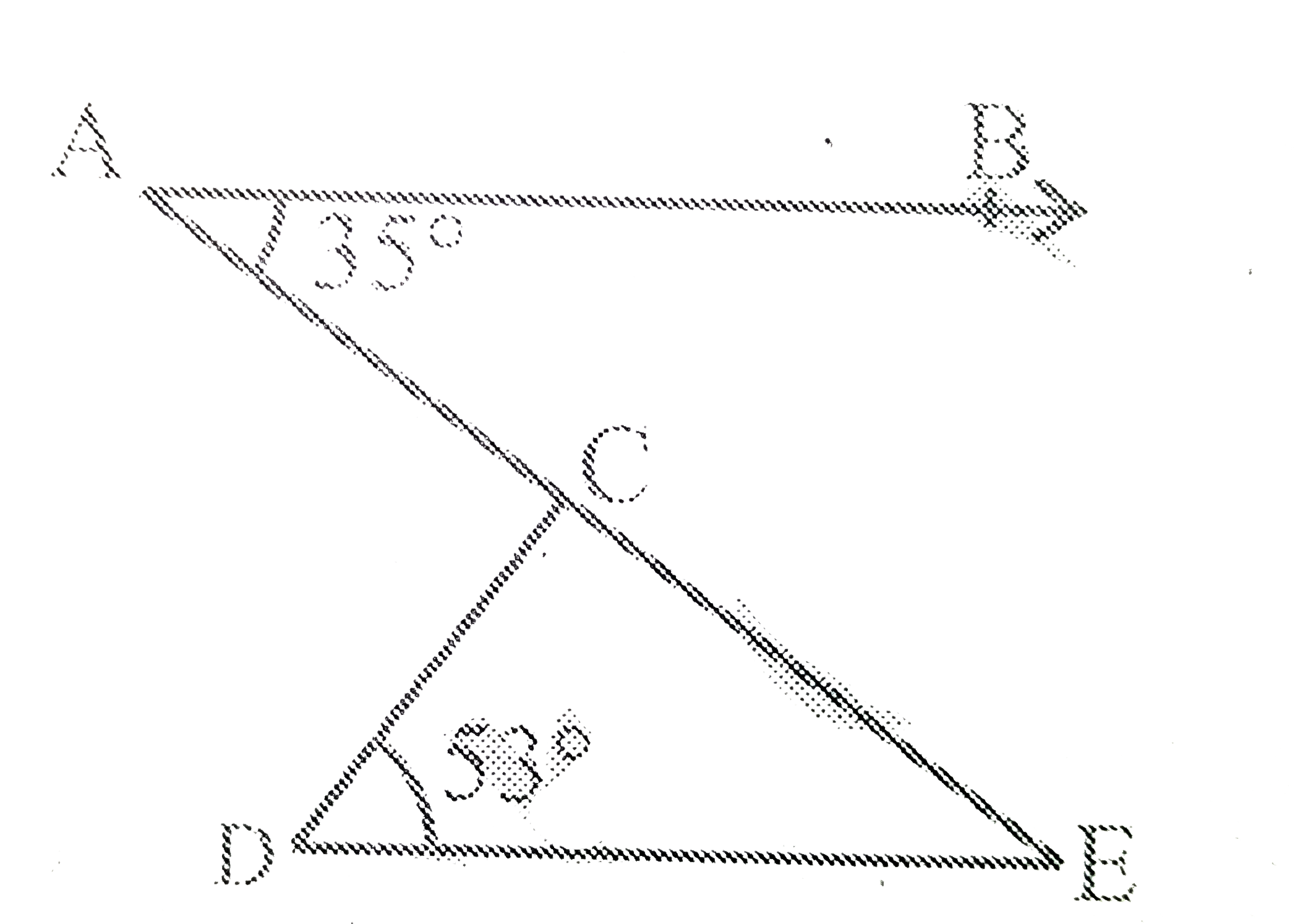
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
View SolutionIn Fig. 4.89, if EDC~EBA, ∠BEC=115o and ∠EDC=70o . Find ∠DEC, ∠DCE, ∠EAB, ∠AEB and ∠EBA . (FIGURE)
View SolutionIn Figure, AC=AE, AB=AD and ∠BAD=∠EAC. Prove that BC=DE
View SolutionIn Figure, if AB ∣∣DE, ∠BAC=350and ∠CDE=530, find ∠DCE.
View SolutionIn Fig. 4.241, DEBC and AD=12BD . If BC=4.5cm , find DE . (FIGURE)
View SolutionIn Figure, if AB∣∣DE,∠BAC=350 and ∠CDE=530 , find ∠DCE.
View SolutionIn Fig.81, side BC of ABC has been produced to D and CEBA. If ∠ABC=650, ∠BAC=550, find ∠ACE, ∠ECD and ∠ACD.
View Solution
