In parallelogram ABCD two points P and Q are taken on diagonal BD such that DP = BQ (set figure). Show that:
(i)ΔAPD≅CQB(ii)AP=CQ(iii)ΔAQB≅ΔCPD(iv)AQ=CP(v)APCQis a parallelogram. ltbegt 
ABCD is a parallelogram and P and Q are lie on BD such that
DP = BQ
(i) We have to show,
ΔAPD≅ΔCQB
Now, in ΔAPDandΔCQB, we have
∵⎧⎪⎨⎪⎩DP=AQ(give)AD=BC(opposite sides of parallelogram)∠1=∠2(alterate angle)
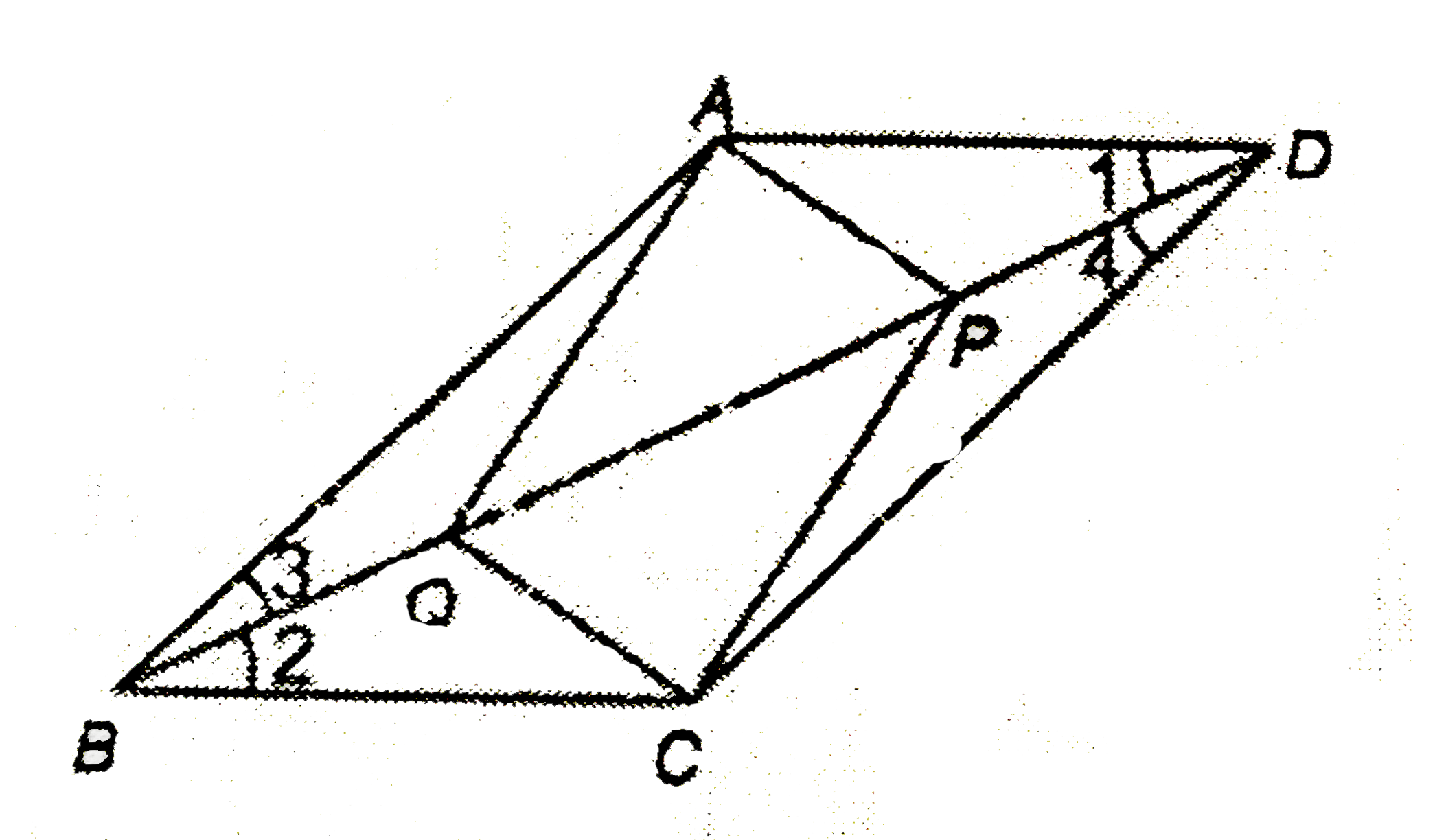
∴ ΔPAD≅ΔCQB (by SAS)
(ii) Since ΔAPD≅ΔCQB (just proved)
∴ AP=CQ
(iii) Here, we have to show, ΔAQB≅ΔCPD
Now, in ΔAQBandΔCPD, we have
∵⎧⎪⎨⎪⎩BQ=DP(given)AB=CD(opposite sides of parallelogram)∠3=∠4(alternate angles)
∴ ΔAQB≅ΔCPD (by SAS)
(iv) since ΔAQB≅ΔCPD
∴ AQ=Cp
(v) Now, since AP = CQ
and AQ = CP
∴□APCQis a parallelogram. (∵pairs of opposite sides are equal)
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b
15 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)
5 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔAQB≅ΔCPD
(iv) AQ=CP
(v) APCQ is a parallelogram.

View SolutionThe given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM=BN
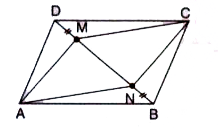 .
.
Prove that:
(i) ΔDMC≅ΔBNA and so CM=AN.
(ii) ΔAMD≅ΔCNB and so AM=CN.
(iii) ANCM is a parallelogram.
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that
(i) ΔAPB≅ ΔCQD
(ii) AP = CQ
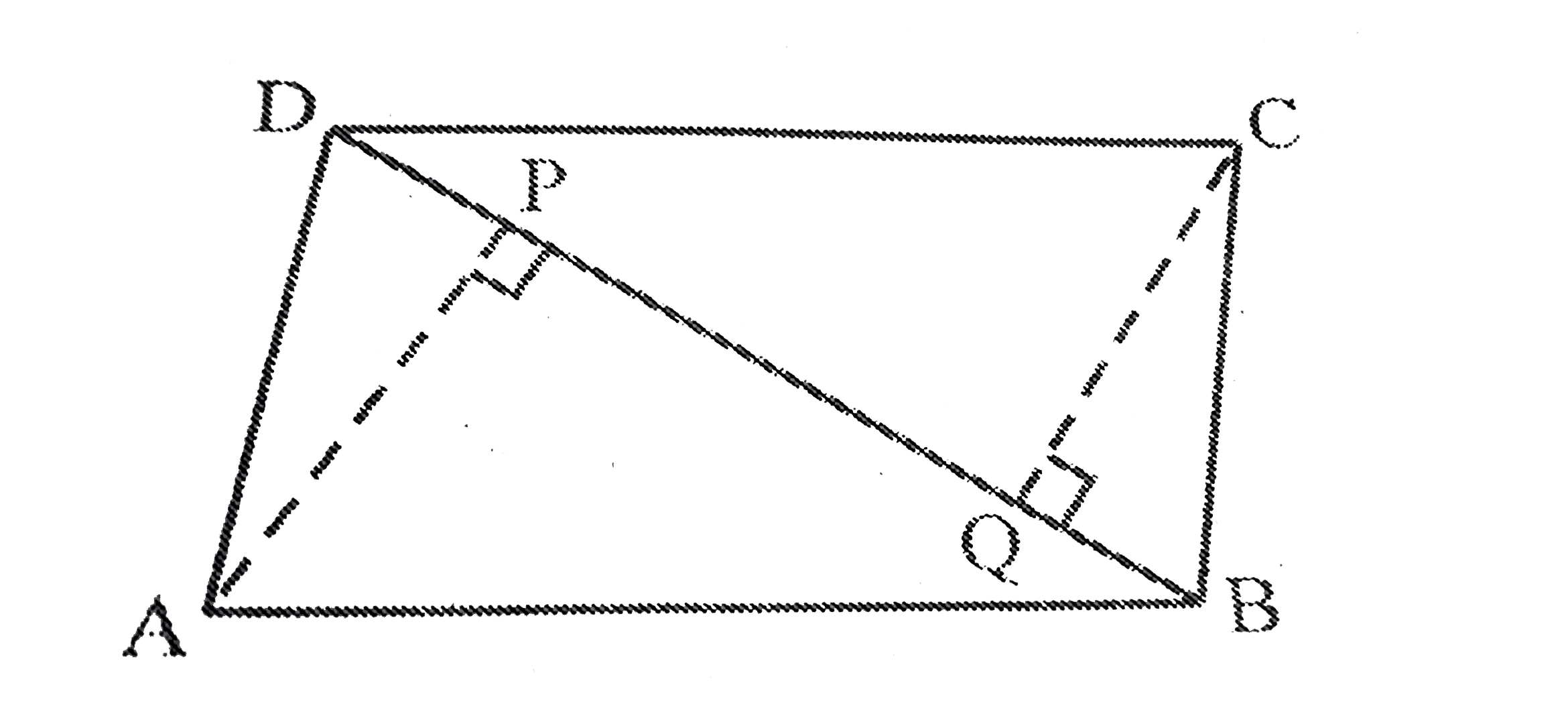
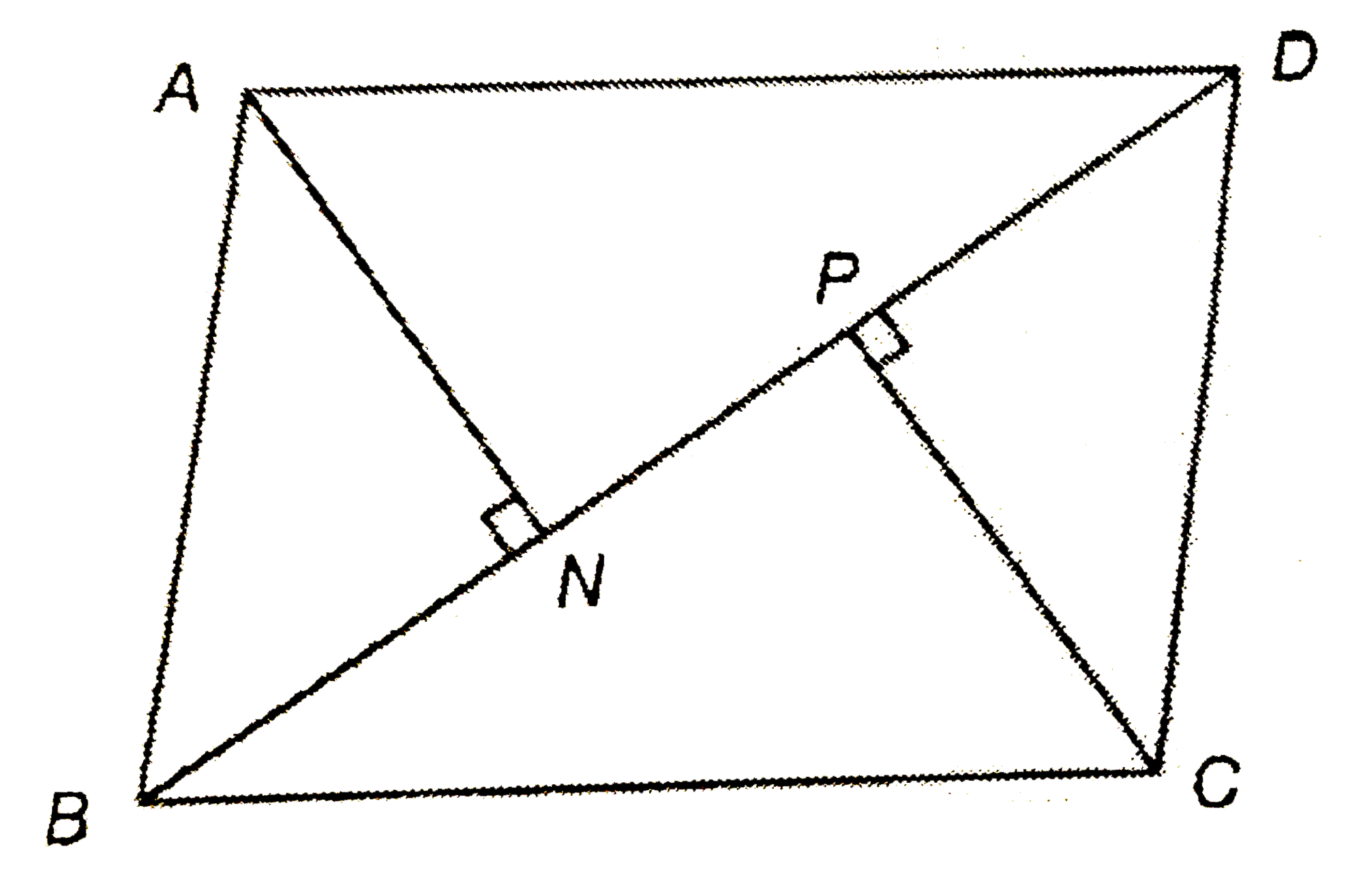
View SolutionIn the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
View SolutionABCD is a parallelogram. Two points P and Q are taken on sides AD and BC respectively such that AP 13ADandCQ=13BC. Prove that □AQCP is a parallelogram.
View SolutionIn parallelogram ABCD, P is a point on side AB and Q is a ponit on side BC.
Prove that :
(i) ΔCPD and ΔAQD are equal in area.
(ii) Area (ΔAQD)
=Area(ΔAPD)+Area(ΔCPB)
View SolutionIn parallelogram ABCD, P is a point on side AB and Q is a ponit on side BC.
Prove that :
(i) ΔCPD and ΔAQD are equal in area.
(ii) Area (ΔAQD)
=Area(ΔAPD)+Area(ΔCPB)
View SolutionABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: (i) APCQ is a parallelogram. (ii) DPBQ is a parallelogram.
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP.
View SolutionIn parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of ΔPOB=40cm2 and OP:OC= 1:2, find :
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
View Solution
