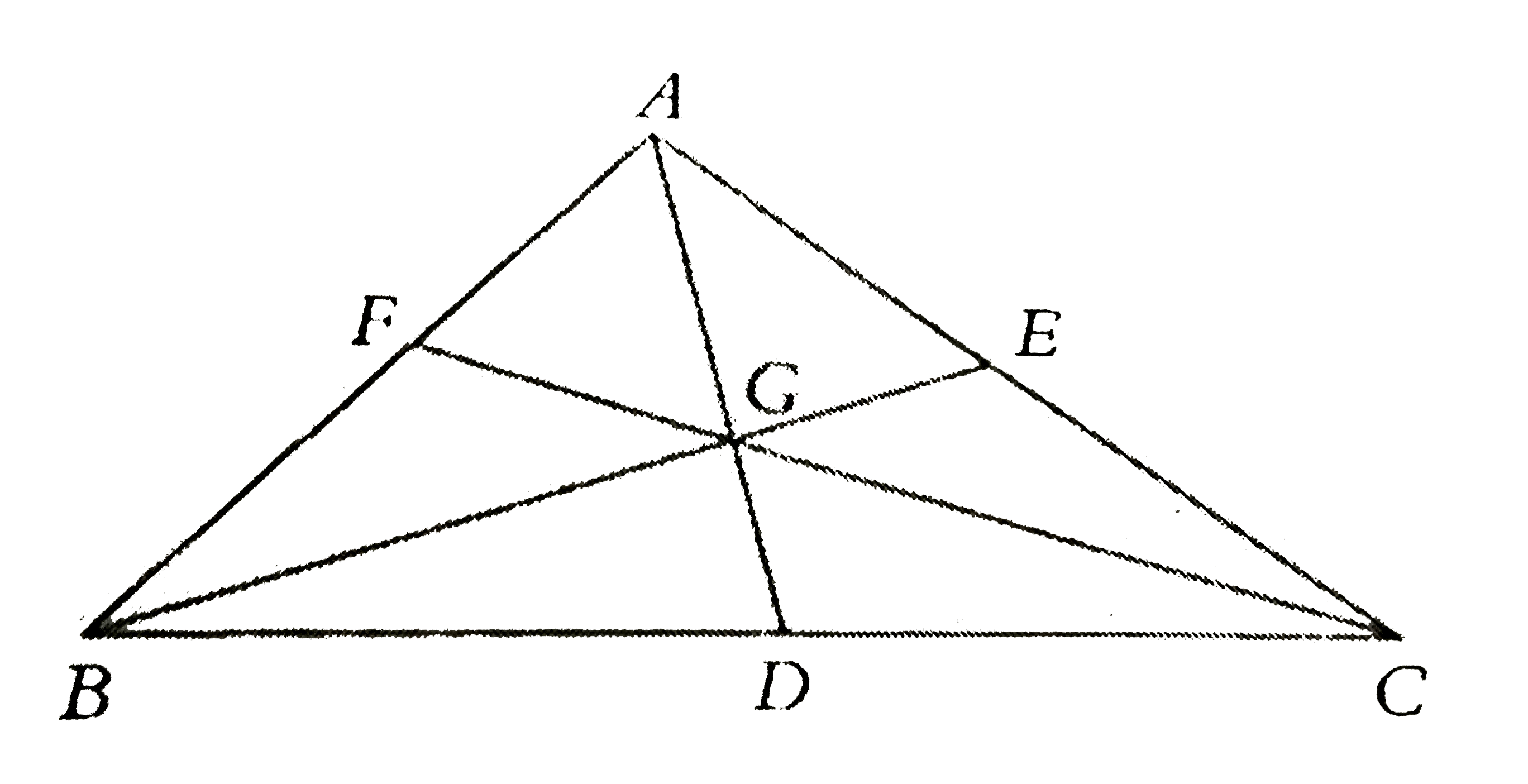
In the above ΔABC,¯¯¯¯¯¯AD,¯¯¯¯¯¯BE,and¯¯¯¯¯¯CF are the medians. G is the centroid. What is the ratio of the areas of ΔBGDandΔGCE?
Step by step video & image solution for In the above DeltaABC, bar(AD),bar(BE) , and bar(CF) are the medians. G is the centroid. What is the ratio of the areas of DeltaBGD and DeltaGCE? by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In ΔABC, the medians AD and BE meet at G. The ratio of the areas of ΔBDG and the quadrilateral GDCE is :
A1:2B1:3C2:3D3:4If G is the centroid of Δ ABC, then ¯¯¯¯¯¯CA+¯¯¯¯¯¯CB =
A3 ¯¯¯¯¯¯GCB3 ¯¯¯¯¯¯CGC3 ¯¯¯¯¯¯ABD3 ¯¯¯¯¯¯GAIn a ΔABC, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of ΔABC=72cm2
A12B16C24D8
In ΔABC,∣∣¯¯¯¯¯¯CB∣∣=a,∣∣¯¯¯¯¯¯CA∣∣=band∣∣¯¯¯¯¯¯AB∣∣=c.CD is the median through the vertex C. Then ¯¯¯¯¯¯CA.¯¯¯¯¯¯CD=
View SolutionLet O be an interior point of ΔABC such that ¯¯¯¯¯¯OA+2¯¯¯¯¯¯OB+3¯¯¯¯¯¯OC=0. Then the ratio of a ΔABC to area of ΔAOC is
View SolutionIn △ABC, the medians AD. BE and CF meet at O. What is the ratio of the area of △ABD to the area of △AOE ?
View SolutionIn △ABC , the medians AD, BE and CF meet at O. What is the ratio of the area of △ABD to the area of △AOE ?
View Solution
In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.
View Solution