In the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC<AB+AC.
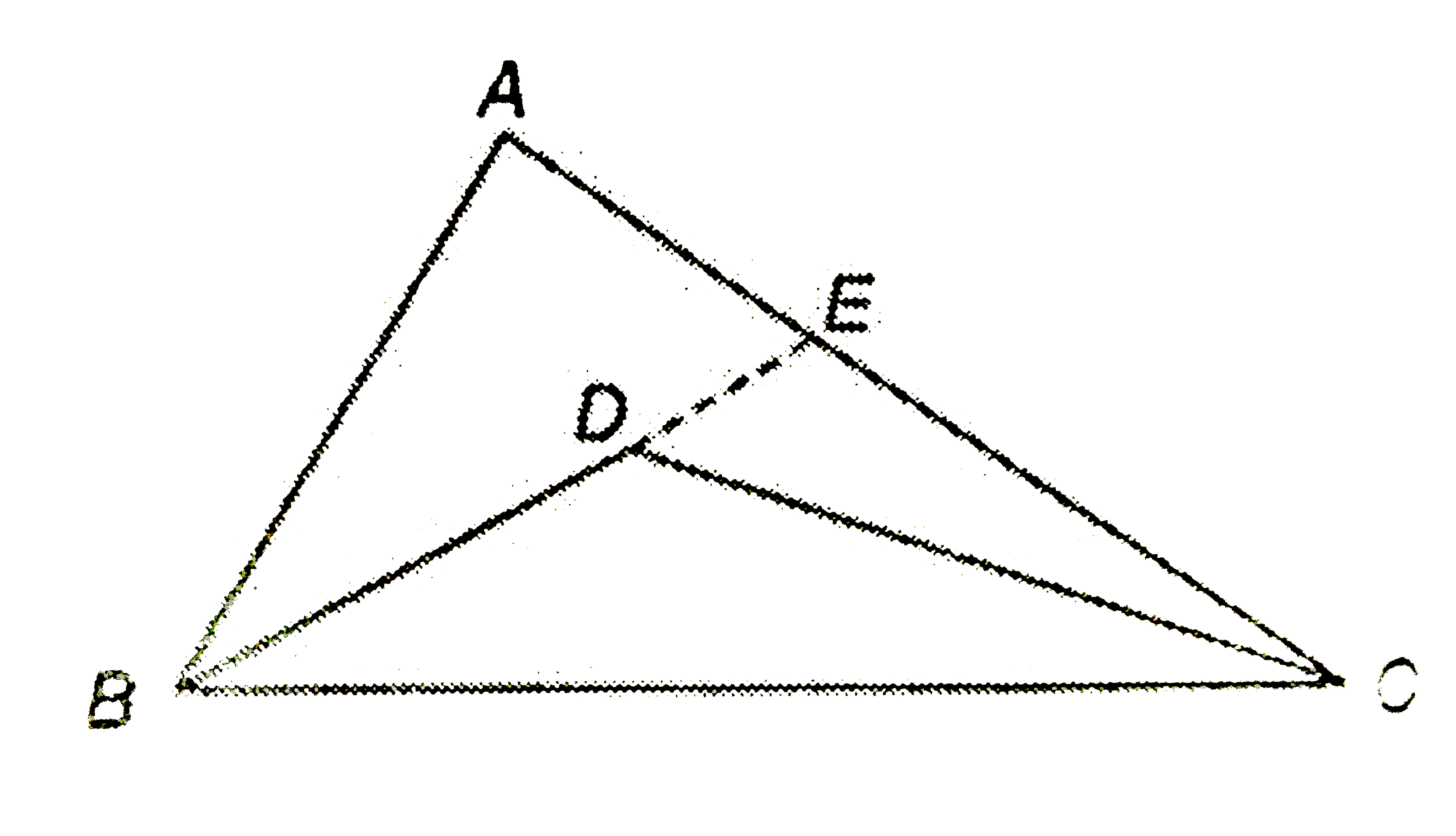
Step by step video & image solution for In the adjoining figure, ABC is a triangle and D is any point in its interior. Show that BD+DC lt AB +AC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.1)14videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.2)9videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - OLYMPAID/ HOTS CORNER10videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner20videos
STATISTICS
Similar Questions
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠A and ∠D
View SolutionIn the adjoinng figure, ΔABC is an isoceless triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠Aand∠D.
View Solution
Knowledge Check
- Question 1 - Select One
D is any point on side AC of a ΔABC with AB=AC then
ACD<BDBCD=BDCCD>BDDNONE
In the adjoining figure, E is a point on the median AD of a ΔABC. Show that ar (ΔABE)=(ΔACE).
View SolutionIn △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)
 View Solution
View SolutionIn the adjoining figure, ABC is a triangle in whcich AB=AC. If D and E are poitns on AB and AC respecrtively such that AD=AE, show that the points B,C,E and D are concyclic.
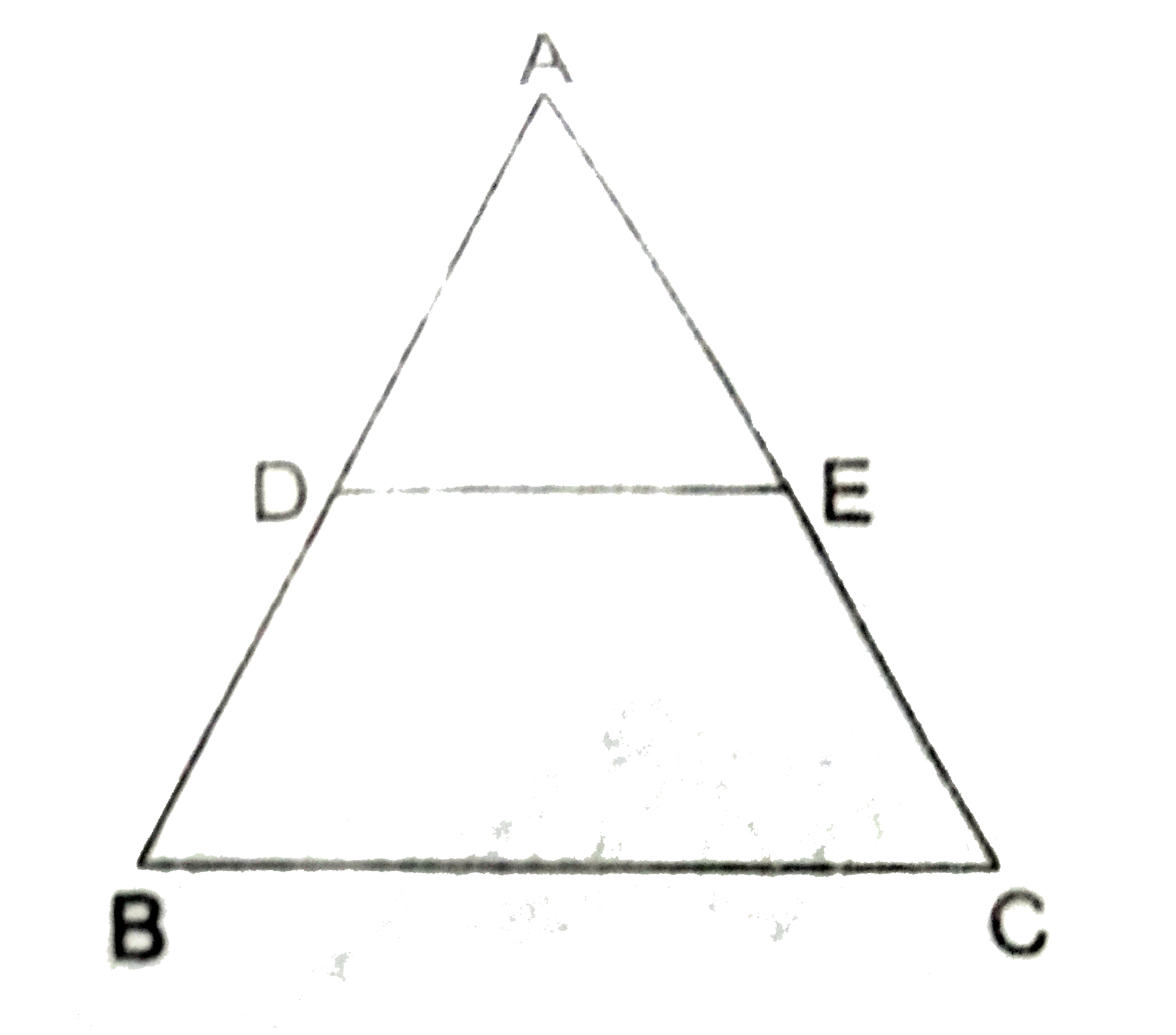 View Solution
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
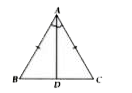
BD = CDView SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that
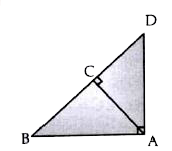
AD2=BD×DCView SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
View Solution
