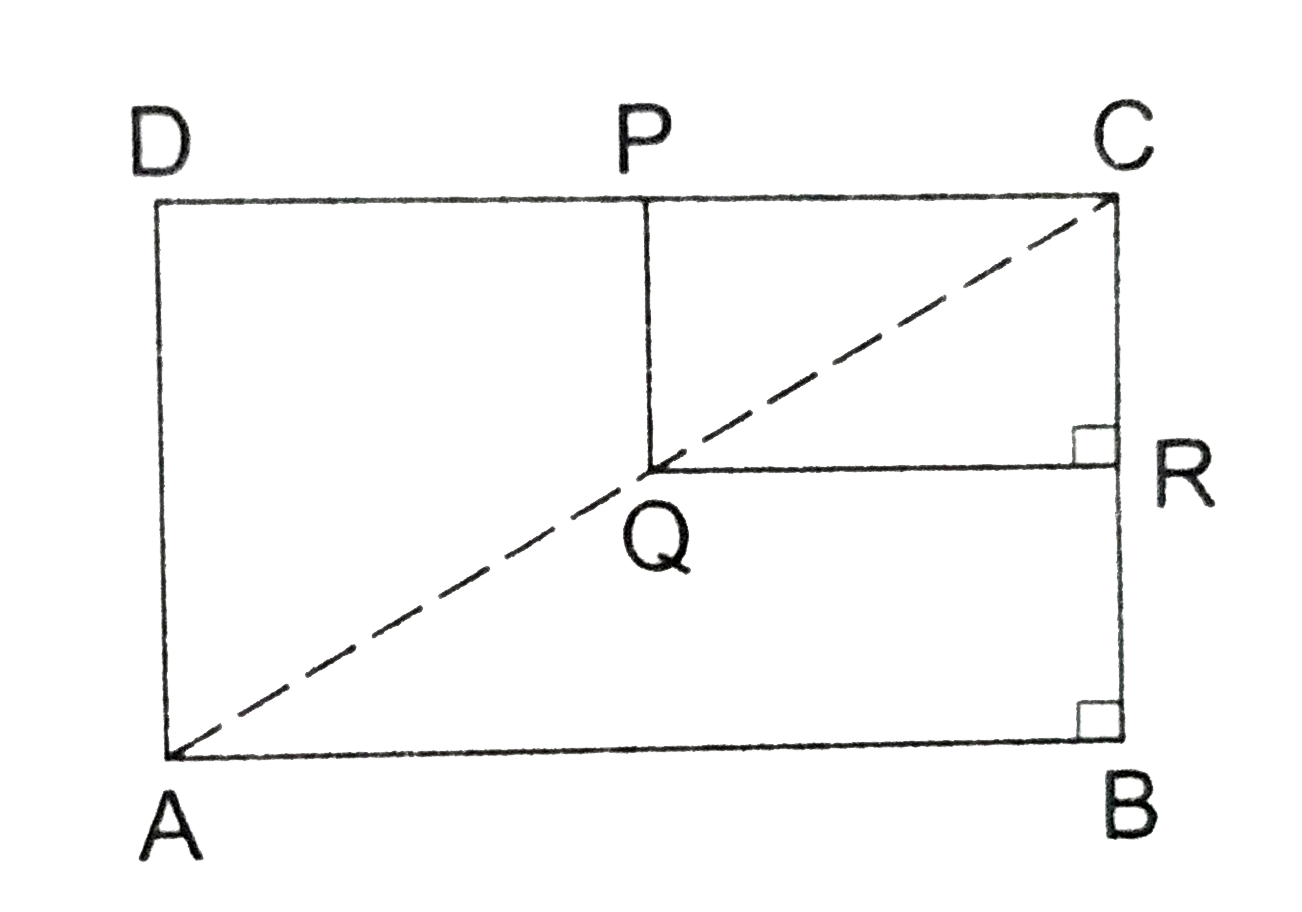
In the adjoining figure, ABCD and PQRC are rectangles, where Q is the midpoint of AC. Prove that
(i) DP=PC, (ii) PR=12AC.
Video Solution
Text Solution
∠CRQ=∠CBA=90∘⇒QR||AB.
In △ABC, Q is the midpoint of AC and QR||AB.
∴ R is the midpoint of BC, i.e., BR = RC.
Similarly, P is the midpoint of DC.
∴DP=PC.
In △CDB, P is the midpoint of DC and R is the midpoint of BC.
∴ PR||DB and PR=12DB=12AC [∵AC=BD].
|
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Knowledge Check
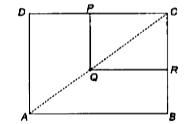
In the given figure, ABCD and PQRC are rectangle, where Q is the mid-point of AC, then DP is equal to
 APCBQACARDQC
APCBQACARDQC
In the adjoining figure if AB+AC=5AD and AC−AD=8 then the area of the rectangle ABCD is
View SolutionIn the adjoining figure PR||AB, PQ||BC and QR||AC. Then what is the relation between AC and QR?
View SolutionIn the given figure, PQ||ABandPR||AC.
Prove that QR∣∣BC
View SolutionIn the adjoining figure, MN∣∣QR.
Find (i) PN and (ii) PR.

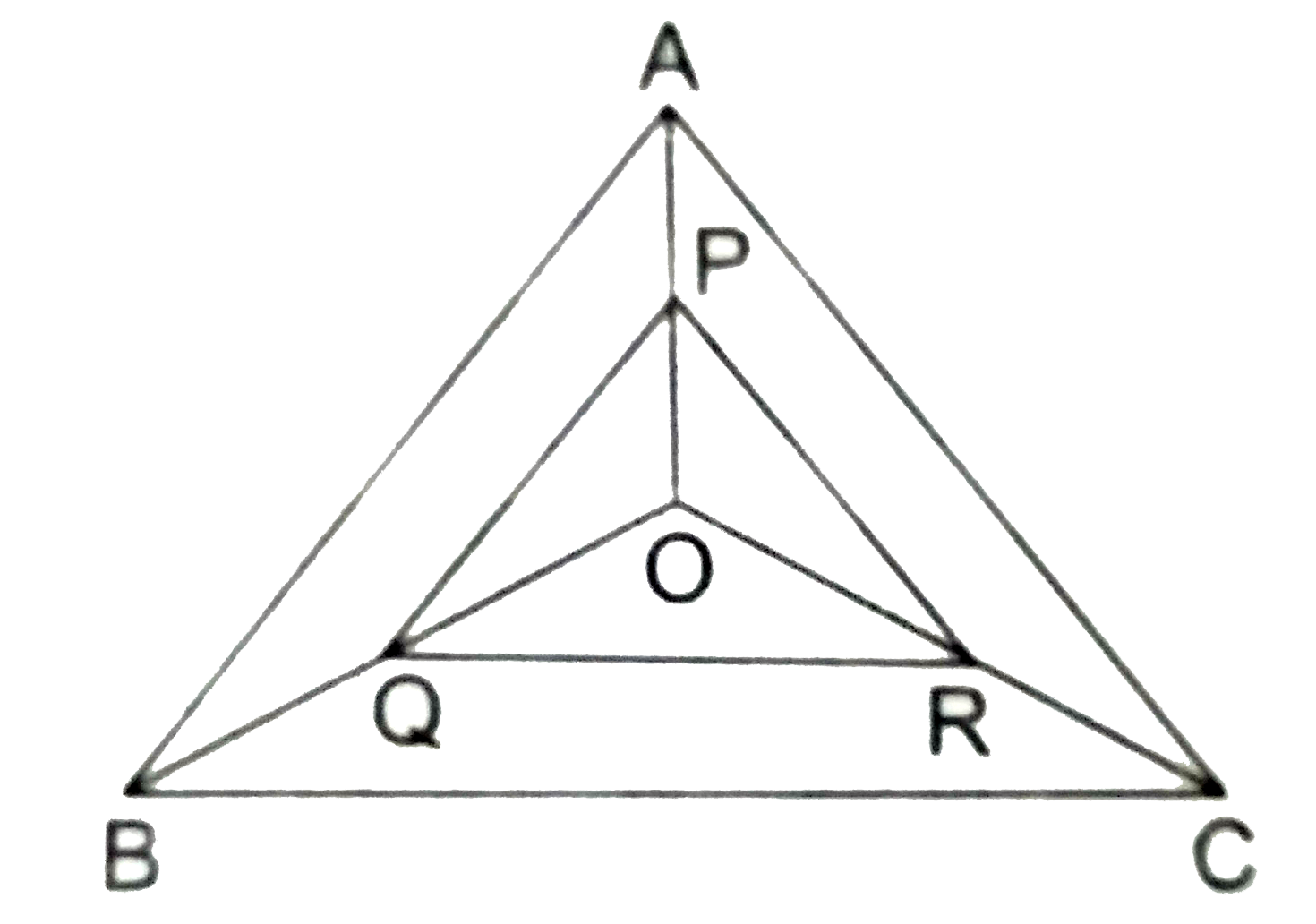
View SolutionIn the adjoining figure. AD and BE and BE are two medians of ΔANC.if DF||BE,then prove thatCG=14AC.
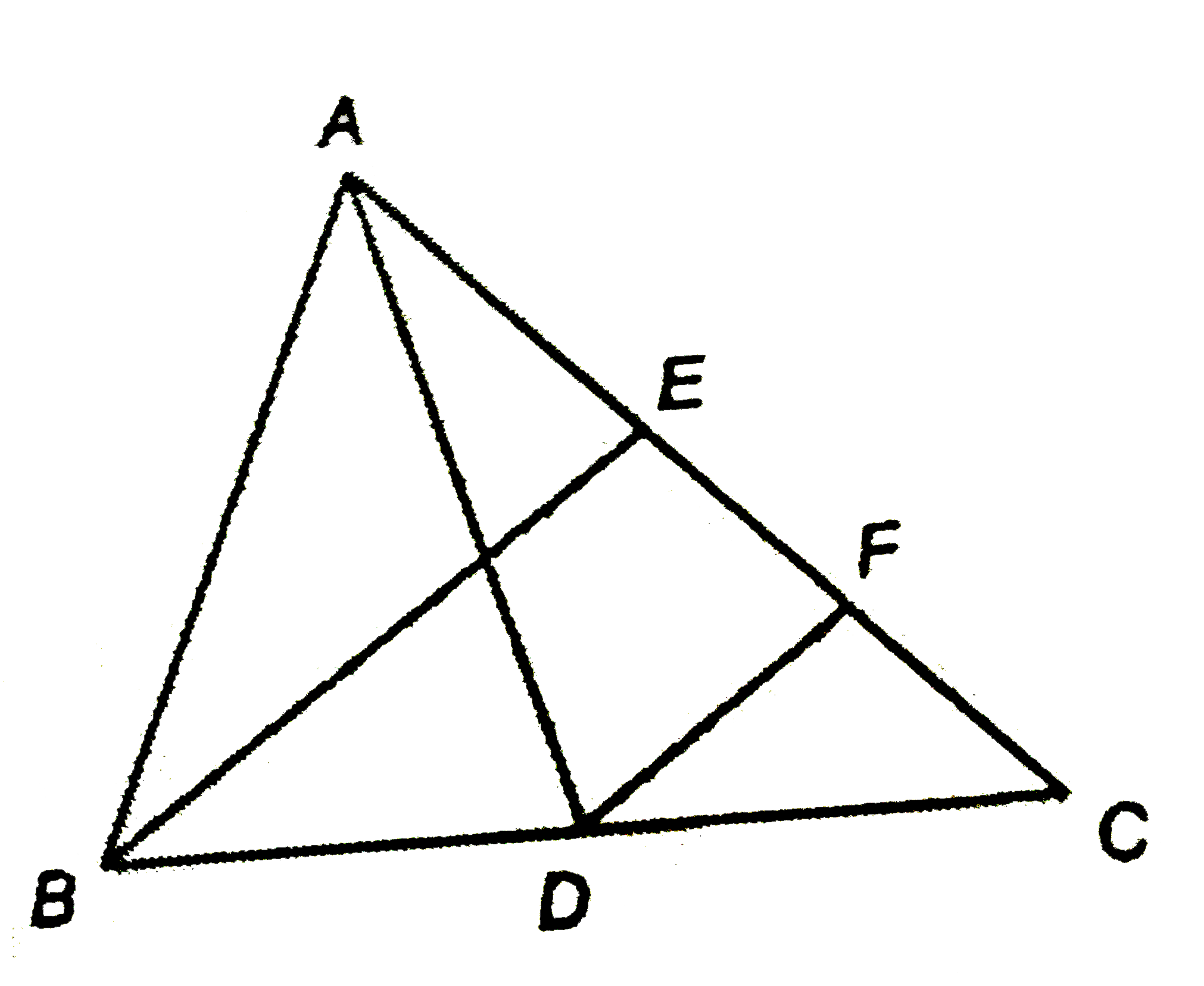
View SolutionIn the adjoining figure,seg DE||side AC and seg DC ||side AP.
Prove that BEEC=BCCP.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View Solution