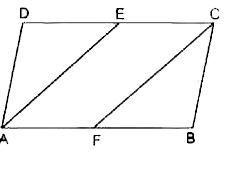
In the adjoining figure, ABCD is a parallelogram and line segments AX and CY bisect ∠Aand∠C respectively. Proove that AX||CY.
Video Solution
Text Solution
We have : ∠A=∠C (opp. ∠ of a|| gm)
⇒12∠A=12∠C⇒∠1=∠2. …(i)
Now, DC||AB and CY is a transversal
⇒∠2=∠3 ...(ii)(alt. interion ∠).
From (i) and (ii), we get ∠1=∠3.
But, these are corresponding angles formed when AX and CY are cut by transversal AB.
∴ AX ||CY.
|
Topper's Solved these Questions
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Exercise 10 A
Explore 10 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:EXERCISE 10B
Explore 27 Videos
- QUADRILATERALSBook:RS AGGARWALChapter:QUADRILATERALSExercise:Matching of Columns:
Explore 2 Videos
- PROBABILITYBook:RS AGGARWALChapter:PROBABILITYExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 10 Videos
Similar Questions
Knowledge Check
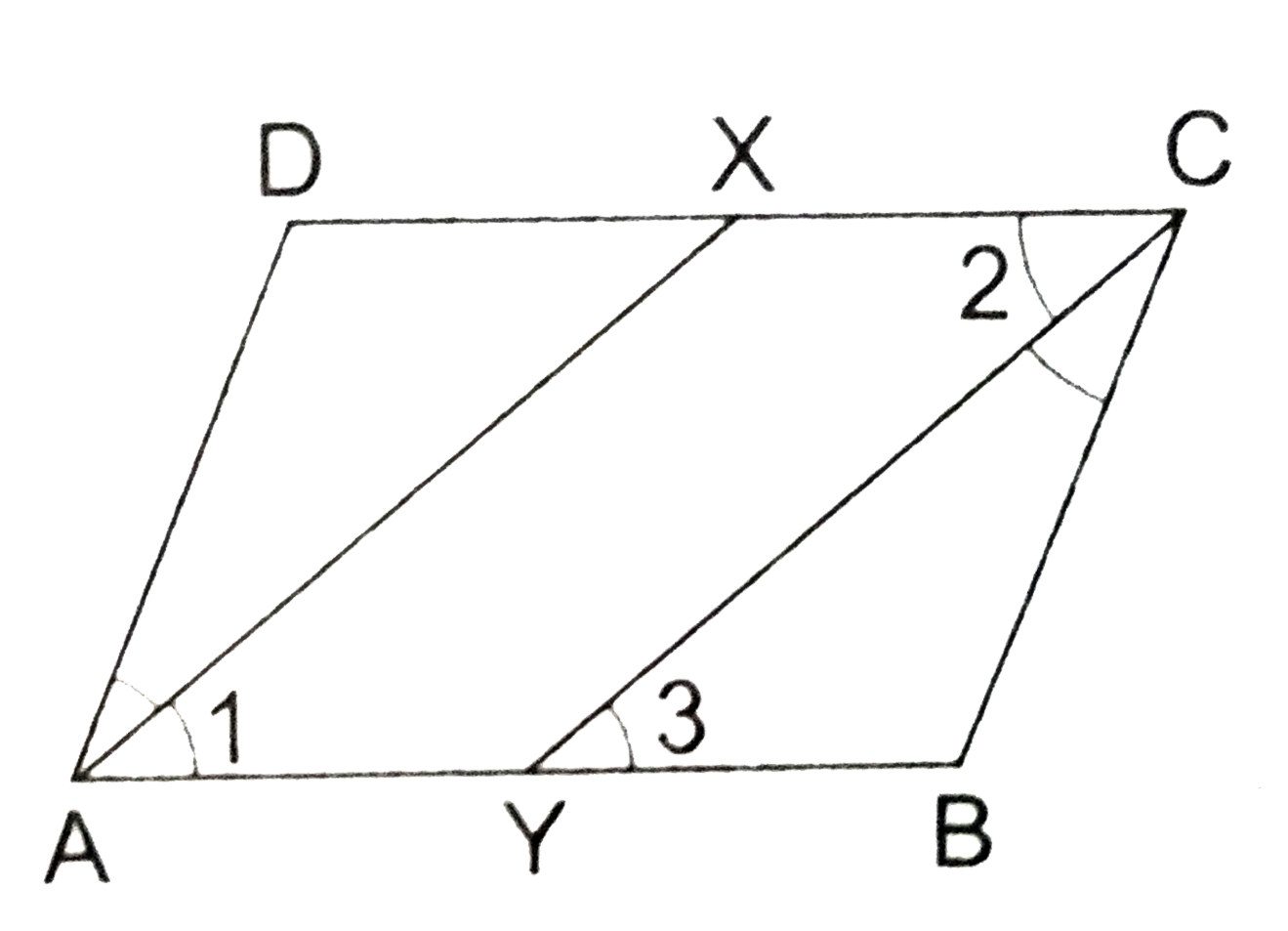
In the adjoining figure, ABCD is a parallelogram. find the measure of ∠BCE.
 A40∘B140∘C60∘D80∘
A40∘B140∘C60∘D80∘In the adjoining figure, ABCD is a parallelogram. Then its area is equal to
 A9 cm2B12 cm2C15 cm2D36 cm2
A9 cm2B12 cm2C15 cm2D36 cm2
ABCD is a parallelogram andline segments AX,CY bisect the angles A and C, respectively Figure. Show that AXCY. Figure
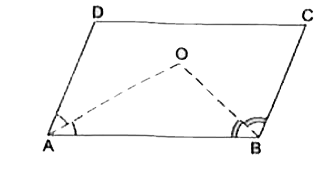
View SolutionIn the adjoining figure, ABCD is a parallelogram , AO and BO are the bisectors of ∠A and ∠B respectively. Prove that ∠AOB=90∘.
View SolutionIn a parallelogram ABCD, AX and CY are the bisectors of ∠Aand∠C respectively. Prove that AX||CY.
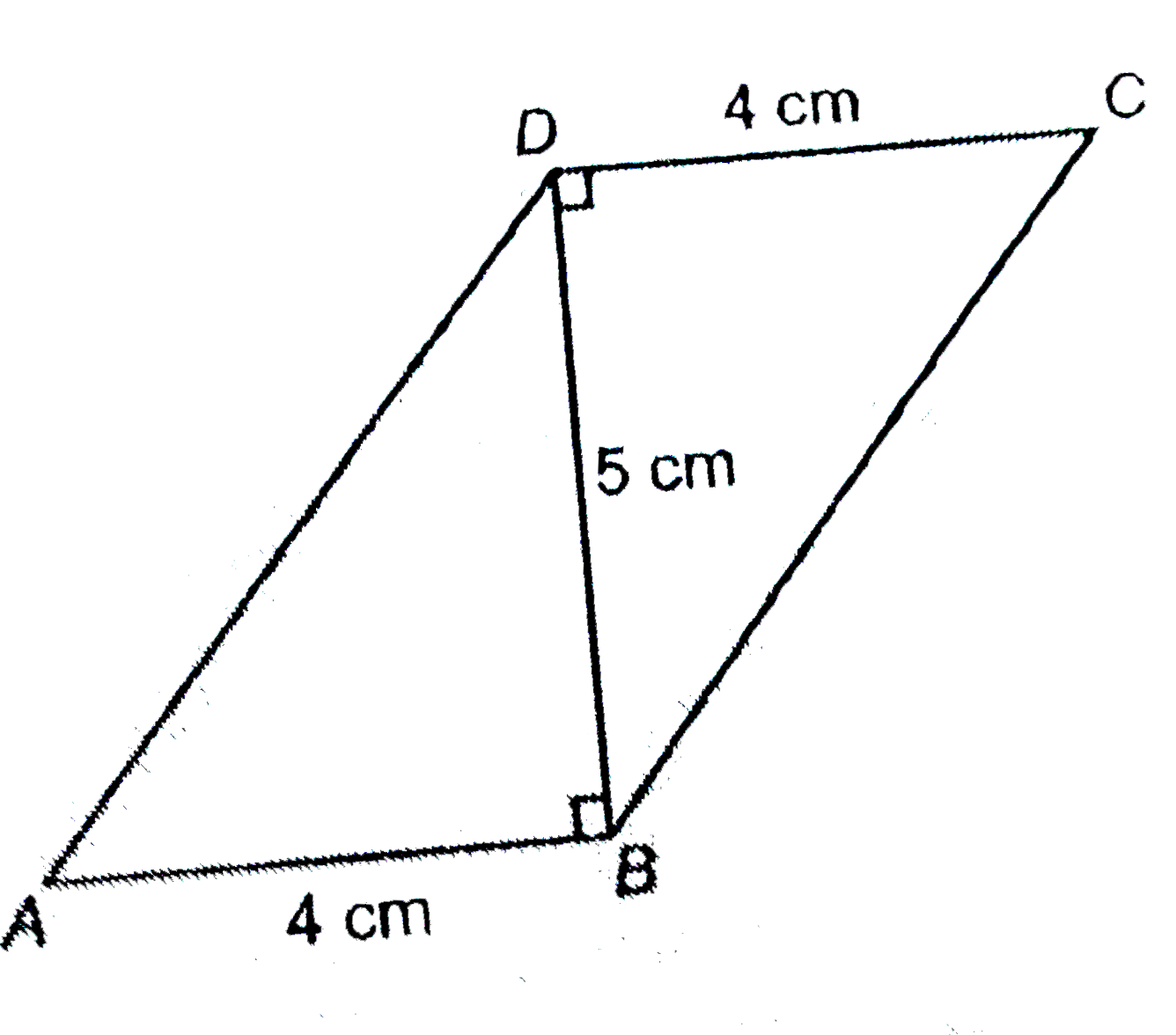
View SolutionIn the adjoining figure, prove that ABCD is a parallelogram. Also find its area.
View SolutionIn the adjoining figure, ABCD is a parallelogram. If ∠MBC=∠NDA, prove that AM=NC.
View SolutionIn the adjoining figure, find the area of the parallelogram ABCD.

View Solution