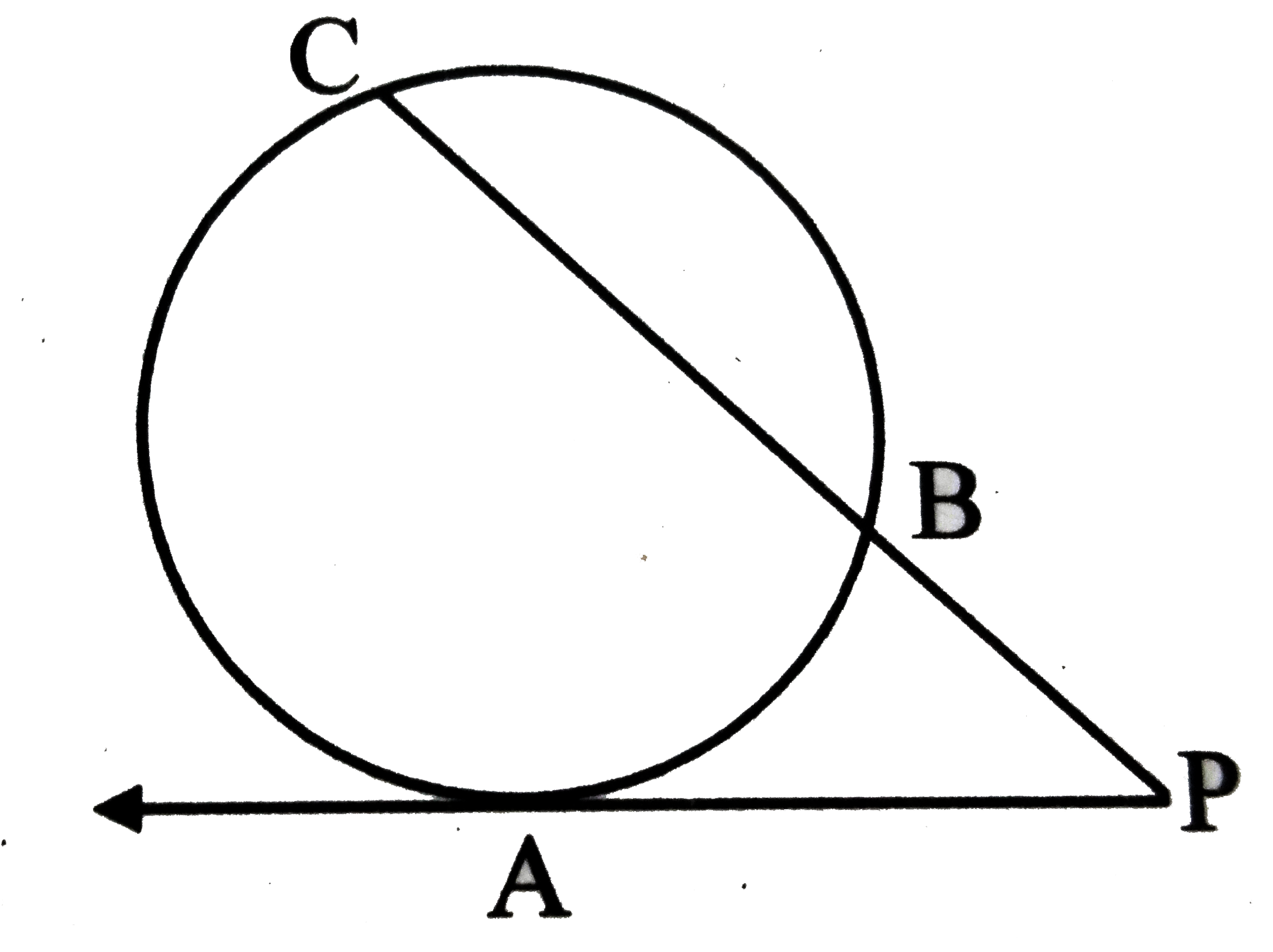
In the adjoining figure, BC is a diameter of the circle with centre M. PA is a tangent at A from P, which is a point on line BC. AD ⊥ BC
prove that DP2=BP×CP−BD×CD
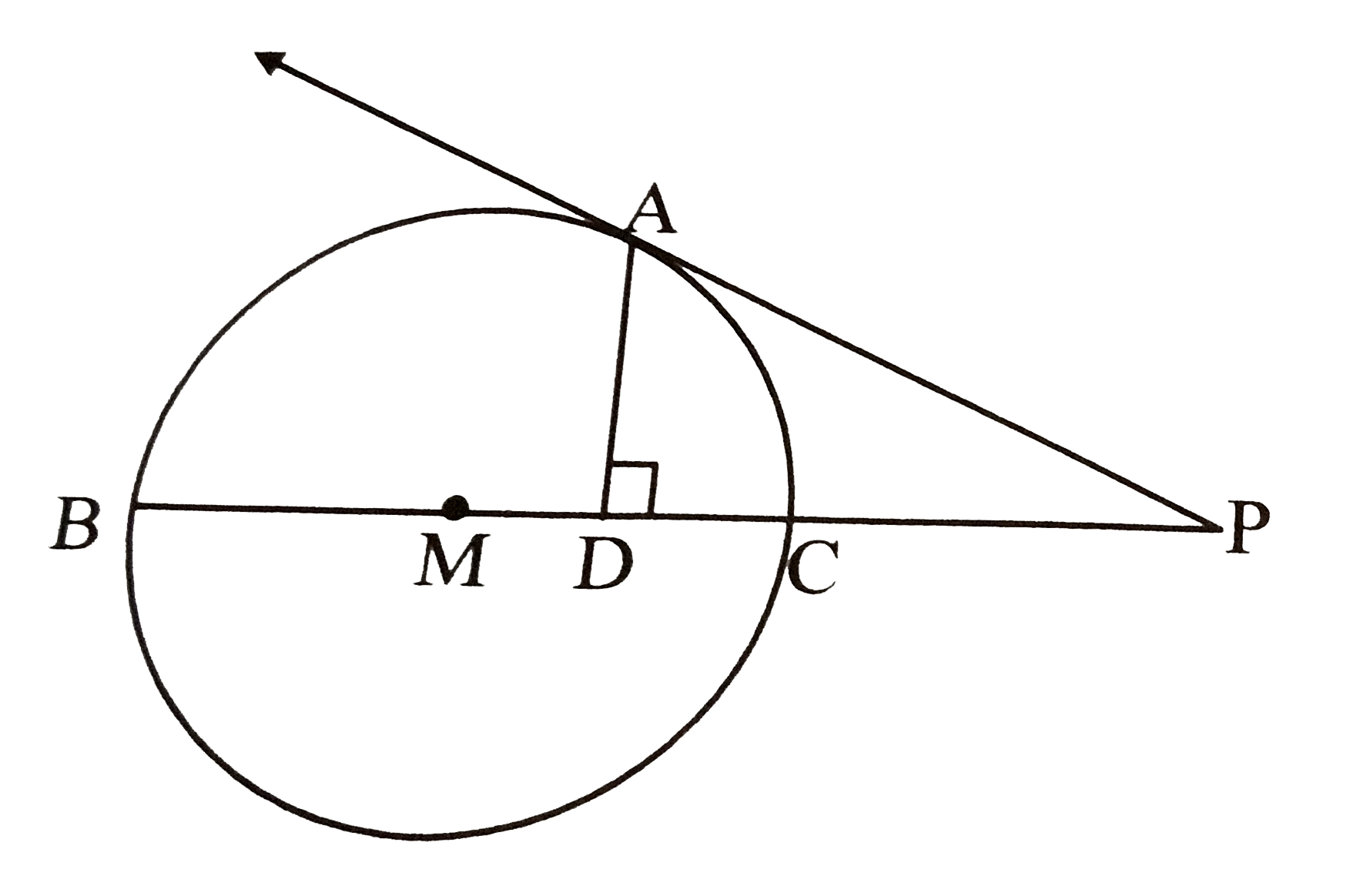
Step by step video & image solution for In the adjoining figure, BC is a diameter of the circle with centre M. PA is a tangent at A from P, which is a point on line BC. AD bot BC prove that DP^(2)=BPxxCP-BDxxCD by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Geometric Constructions
2 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Co-ordinate geometry
13 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Pythagoras theorem
1 Videos
- BOARD QUESTION PAPER: MARCH 2019BOOK - TARGET PUBLICATIONCHAPTER - BOARD QUESTION PAPER: MARCH 2019EXERCISE - (Solve the following questions (Any one):
4 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Chapter Assessment
9 Videos
Similar Questions
Knowledge Check
In the given figure, AB and AC are tangents to the circle with centre O. Given that ∠BAC=70∘ and P is a point on the minor are BC, find ∠ BPC.
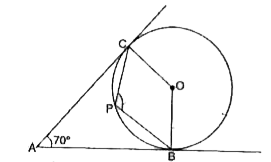 A110∘B140∘C125∘D136∘
A110∘B140∘C125∘D136∘In the following figure, O is the centre of the circle. AB and CD are equal chords. If ∠AOB=100∘ , Find the ∠CED.
 AAC+AB=BCB3AE=AB+BC+ACCAB+BC+AC=4AED2AE=AB+BC+AC
AAC+AB=BCB3AE=AB+BC+ACCAB+BC+AC=4AED2AE=AB+BC+AC
In the figure, BC is a chord of the circle with centre o and A is a point on the minor are BC. Then ∠ABC−∠OBCis equal to
View SolutionIn the adjoining figure, O is the centre of the circle and AB is its diameter. If AC=8 cm and BC= 6cm, then find the radius of the circle.

View SolutionIn the following figure, ray PA is the tangent to the circle at point A and PBC is a secant. If AP = 14, BP = 10, then find BC.
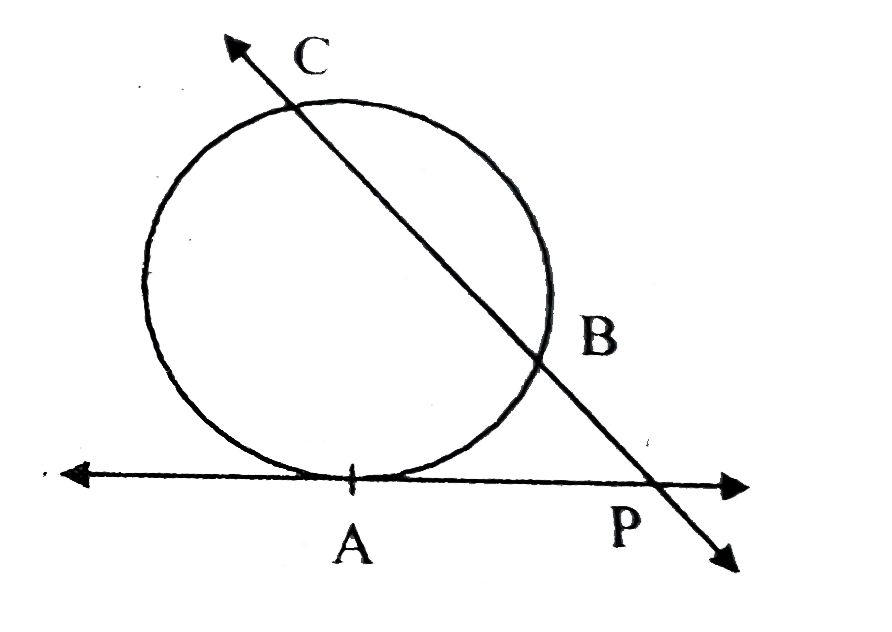
View SolutionA Δ ABC is right angled at A. L is a point on BC such that AL⊥ BC. Prove that ∠BAL=∠ACB.
View SolutionIn the adjoining figure, ABC is a triangle in which AD is the bisector of ∠A. If AD⊥BC, show that △ABC is isosceles.

View SolutionIn the following figure , ray PA is the tangent to the circle at point A and PBS is secant . If AP=14,BP=10, find BC.
View Solution