In Figure, BC is a tangent to the circle with centre O.OE bisects AP. Prove that AEO~ABC.
We have,
OA=OP(Radius of the circle)
∠OEA=900
∠ABC=900 ( tangent to the circle is perpendicular to the radius through the point of contact )
∴∠OEA=∠ABC (Right angle)
∴∠Ais the common angle to both triangle
∴△AOE≅△ABC (by ASA congruence)
Topper's Solved these Questions
Similar Questions
In Figure, BC is a tangent to the circle with centre O.OE bisects AP. Prove that AEO~ABC.
View SolutionIn Fig. 10.64, BC is a tangent to the circle with centre O.OE bisects AP. Prove that ΔABC~ΔAEO
View SolutionIn Figure, AB=CB and O is the centre of the circle. Prove that BO bisects ∠ABC.
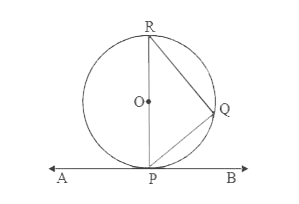
View SolutionIn the given figure, AB is a tangent to a circle with centre O. Prove ∠BPQ=∠PRQ.
View SolutionIn Figure, XPandXQ are tangents from X to the circle with centre O.R is a point on the circle. Prove that, XA+AR=XB+BR
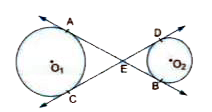
View SolutionIn Fig common tangents AB and CD to two circles with centres O1andO2 intersect at E. Prove that AB = CD.
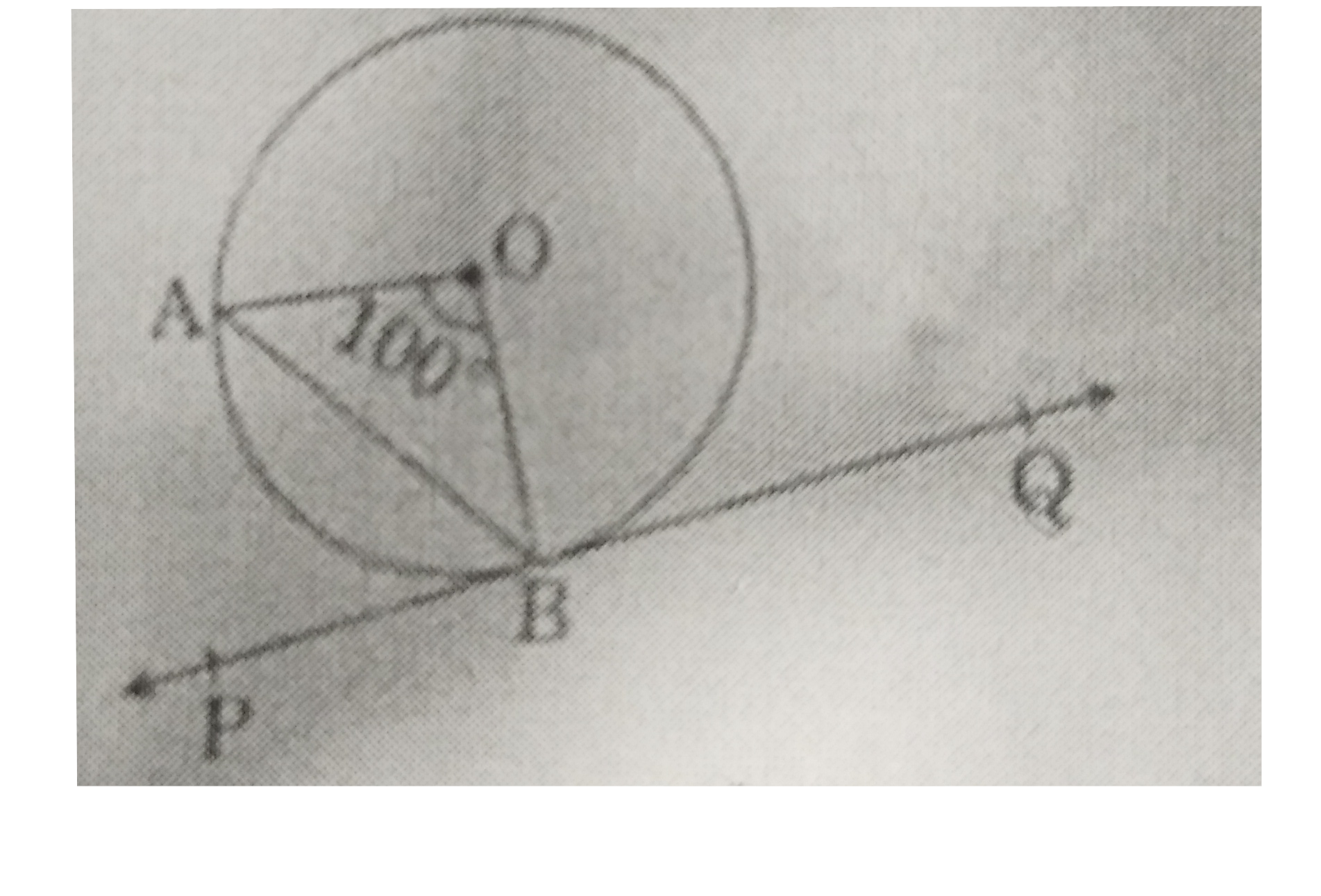
View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to
View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
View SolutionIn Figure, two tangents ABandAC are drawn to a circle with centre O such that ∠BAC=1200. Prove that OA=2AB
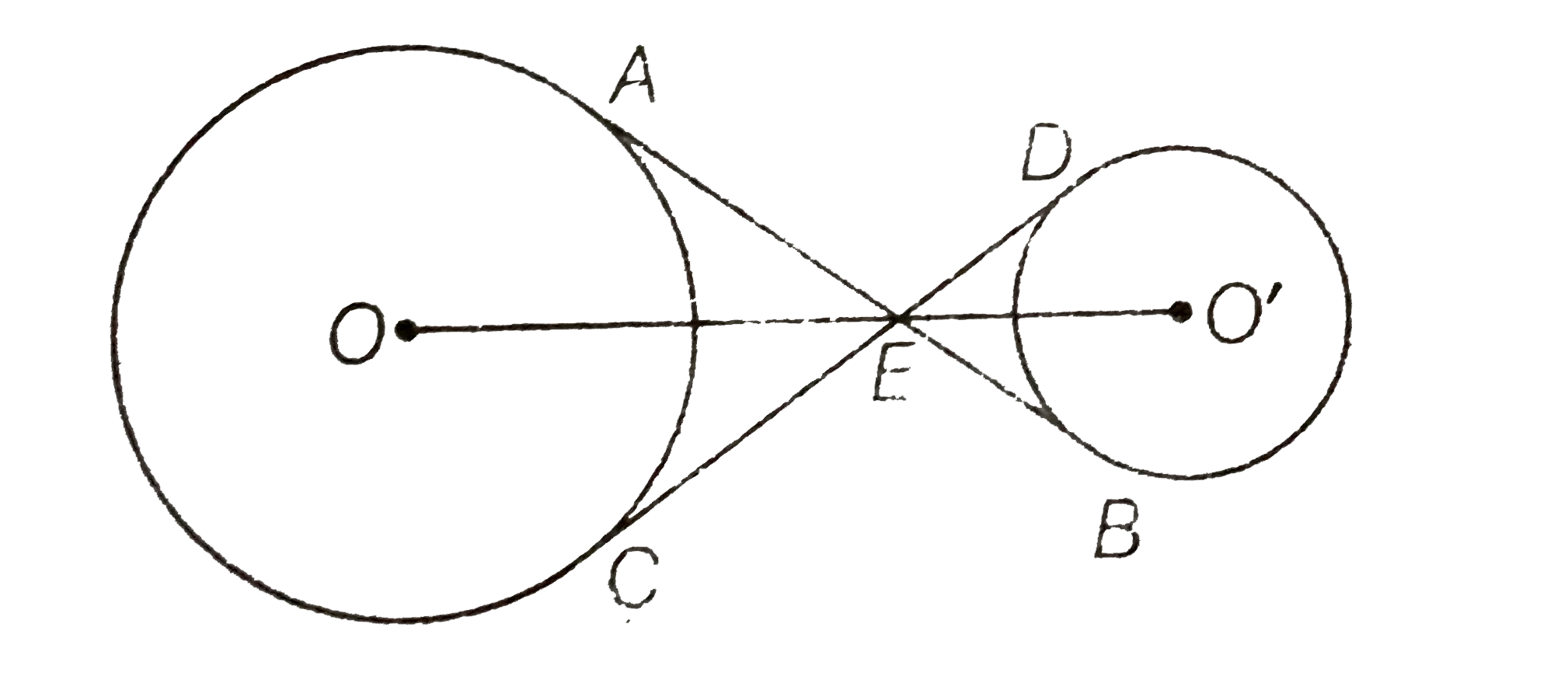
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
View Solution