In the adjoining figure, line AP is tangent to the circle at A, secant through P intersects chord AY in point X such that AP=PX=XY.
IF PQ=1 and QZ=8, then find AX.
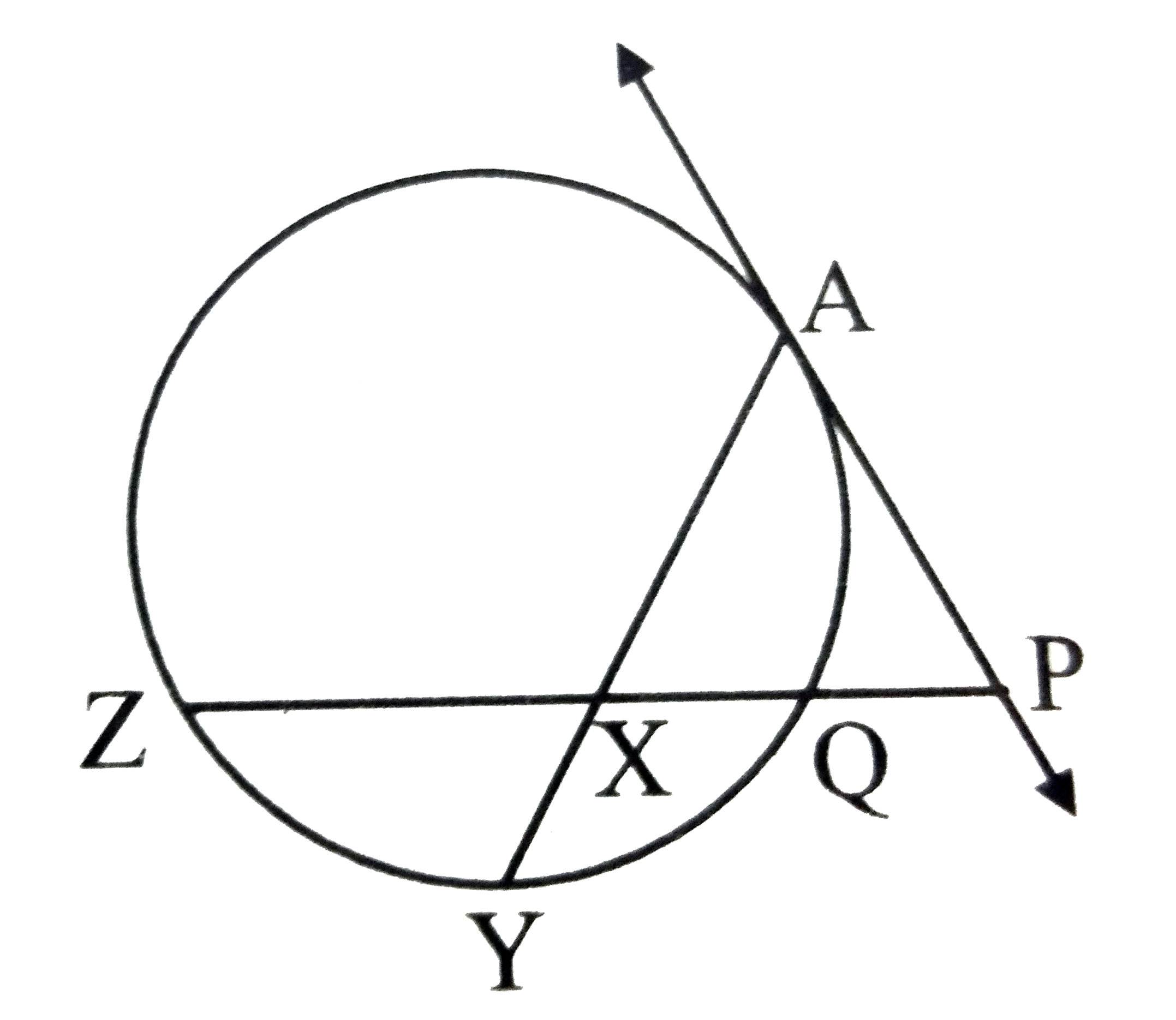
The correct Answer is:3 units
Step by step video & image solution for In the adjoining figure, line AP is tangent to the circle at A, secant through P intersects chord AY in point X such that AP=PX=XY. IF PQ=1 and QZ=8, then find AX. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Chapter Assessment9videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Multiple Choice Question25videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics4videos
CHALLENGING QUESTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT19videos
CO-ORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at N and R. PQ=15cm,PR=25cm, find PN:
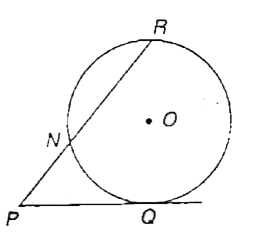 A15 cmB10 cmC9 cmD6 cm
A15 cmB10 cmC9 cmD6 cm
In the figure, a tangent segment PA touches the circle at point A and secant PBC intersects the circle at points B and C. If AP=15 cm and BP=10, then find BC.
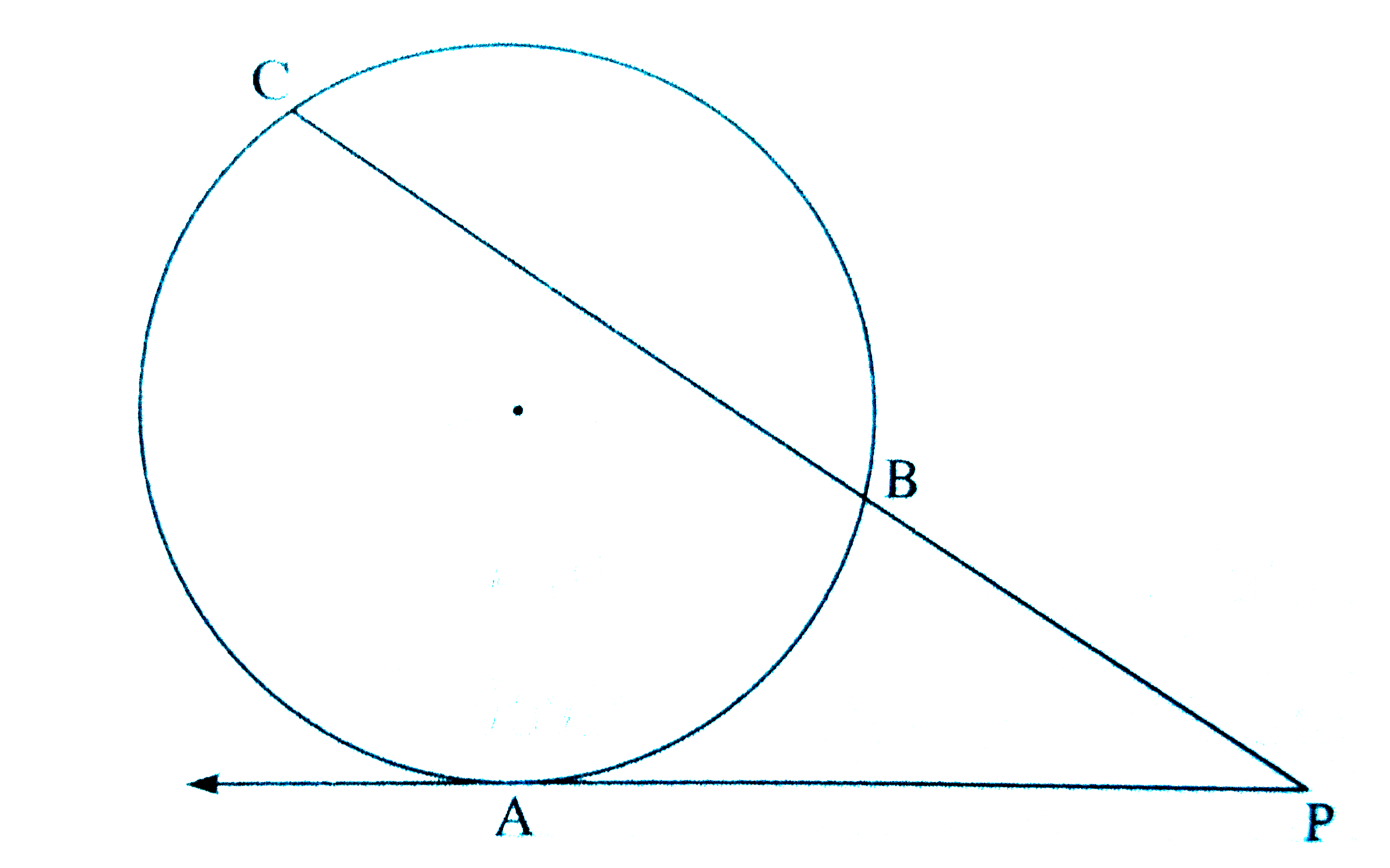 View Solution
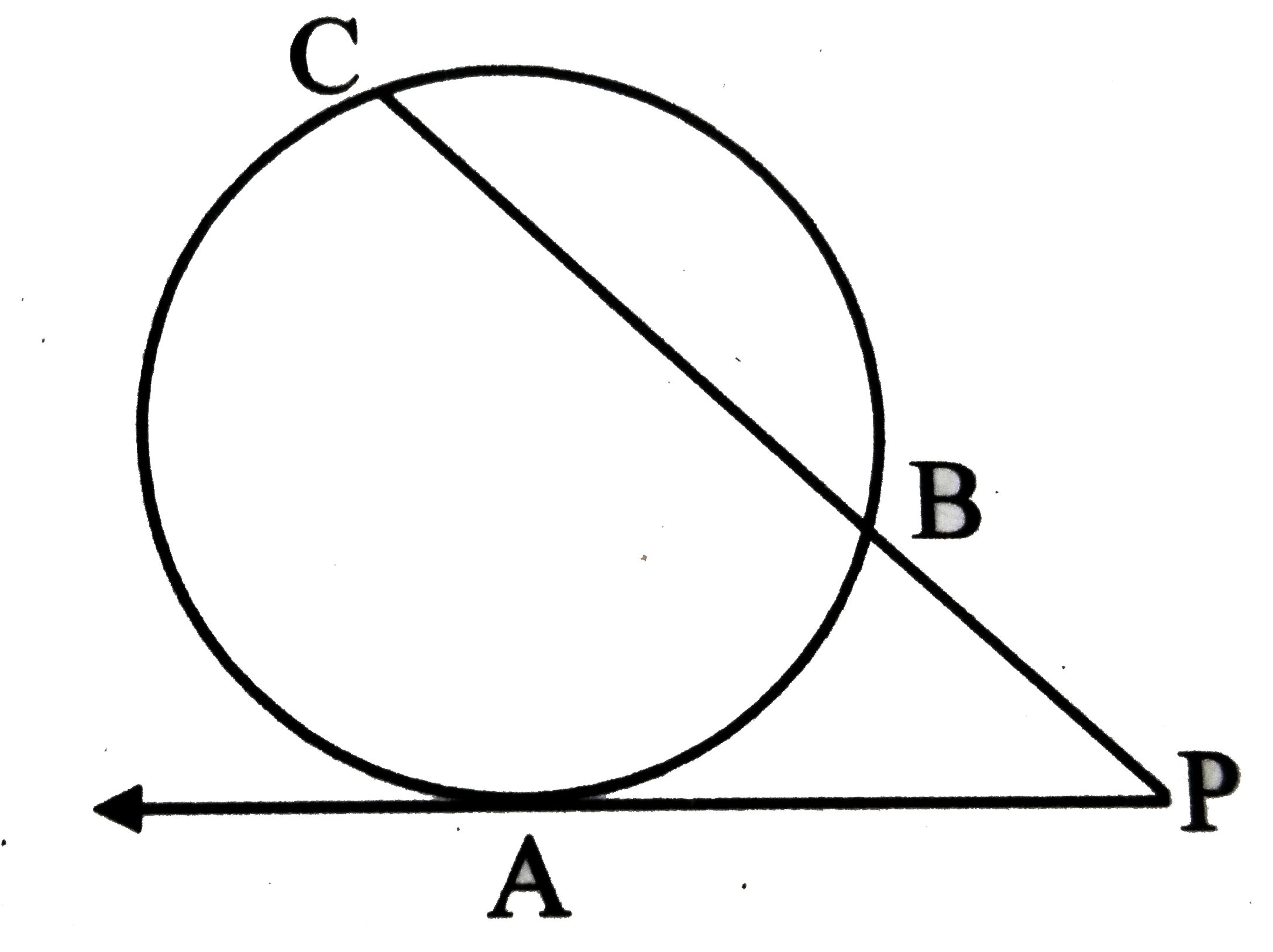
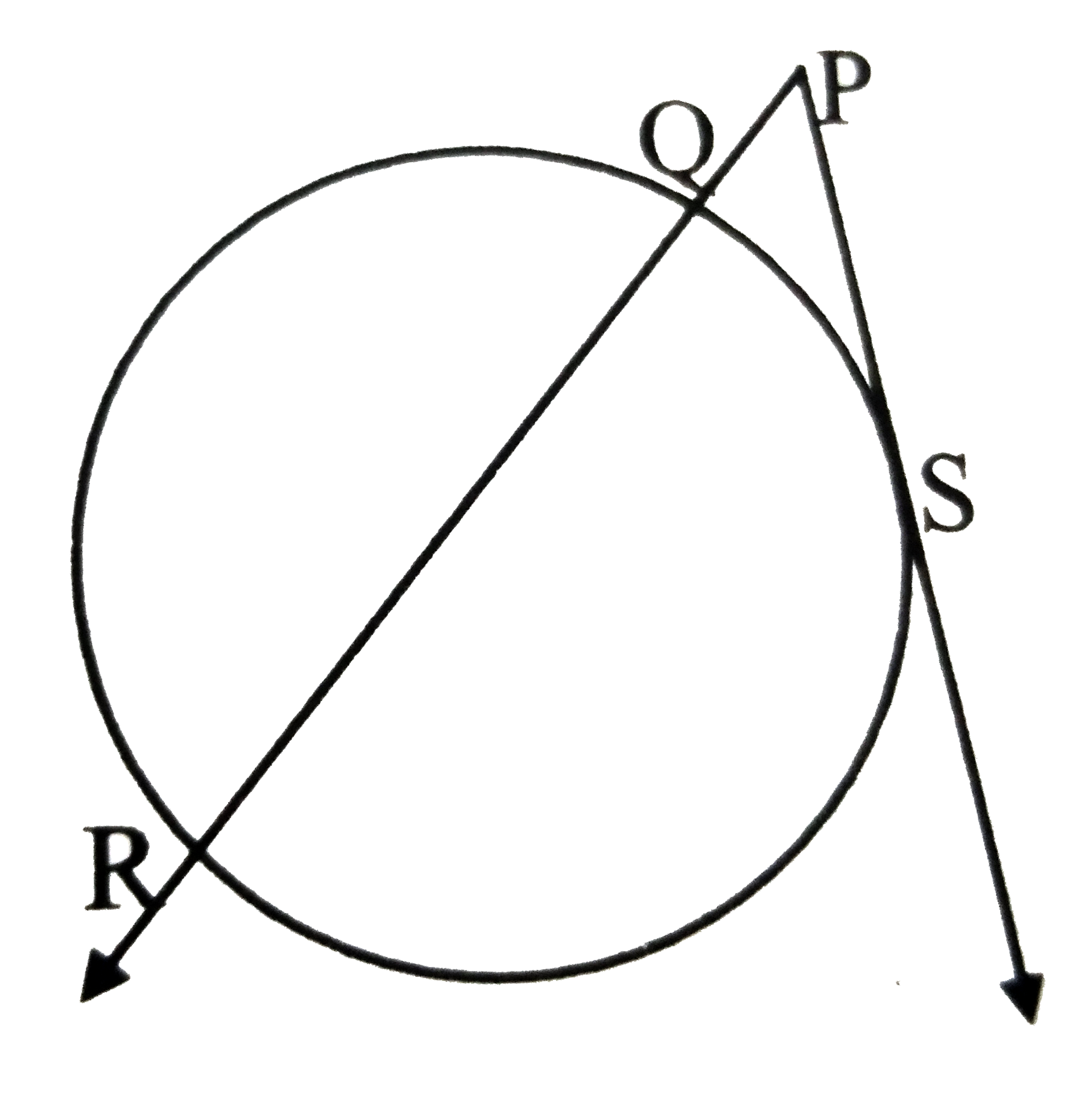
View SolutionIn the following figure , ray PA is the tangent to the circle at point A and PBS is secant . If AP=14,BP=10, find BC.
 View Solution
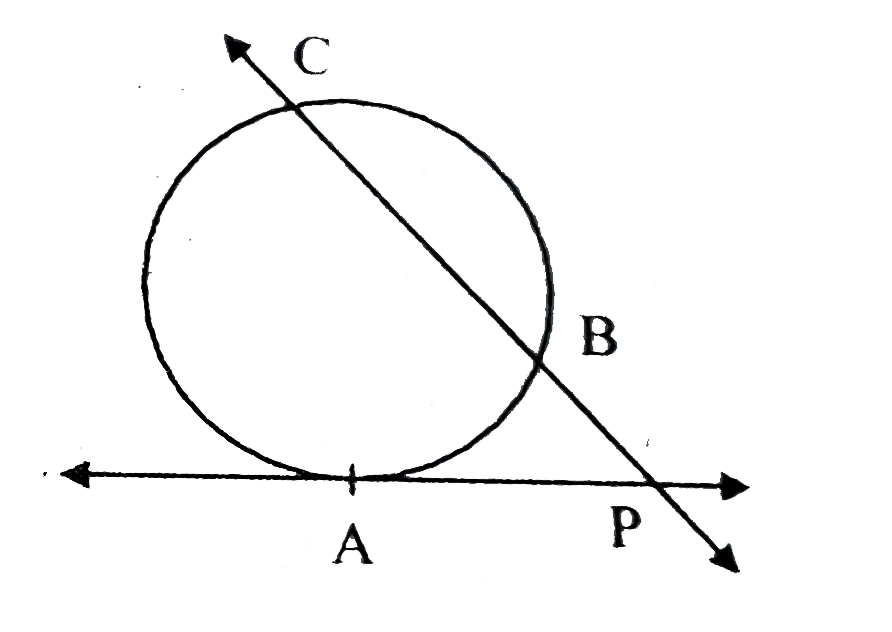
View SolutionIn the adjoining figure ,seg PS is a tangent segment. Line PR is a secant. If PQ=3.6, and QR=6.4, find PS.
 View Solution
View SolutionIn the following figure, ray PA is the tangent to the circle at point A and PBC is a secant. If AP = 14, BP = 10, then find BC.
 View Solution
View SolutionA line passing through P(1,2) intersect the line x+y+3=0 in point A such that AP=3√2 then slope of AP is
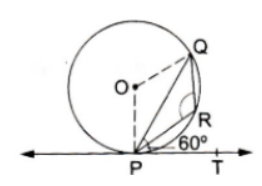
View SolutionIn the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT=60∘.Find ∠PRQ.
 View Solution
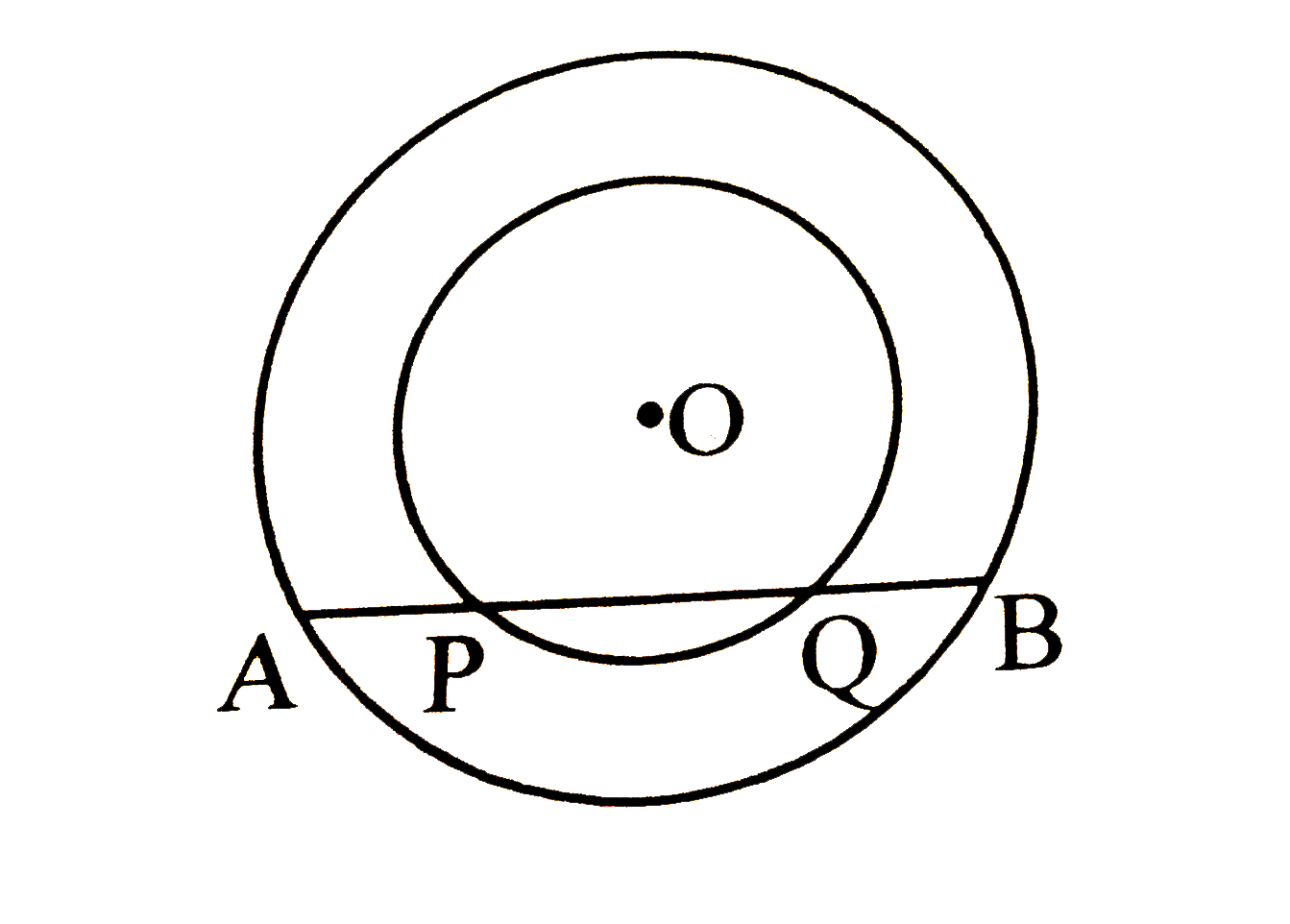
View SolutionIn the given figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q . Show that AP = BQ.
 View Solution
View Solution


