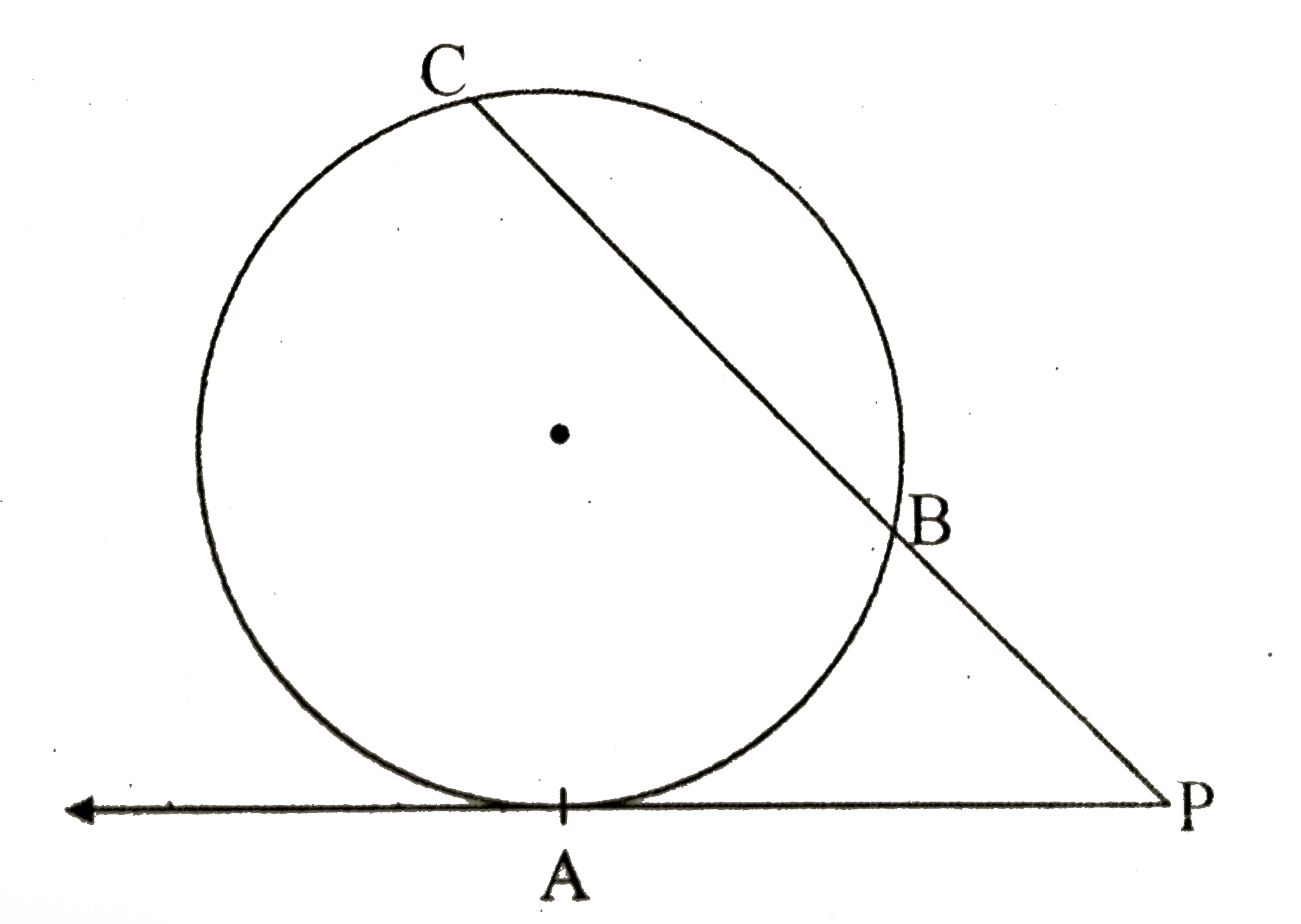
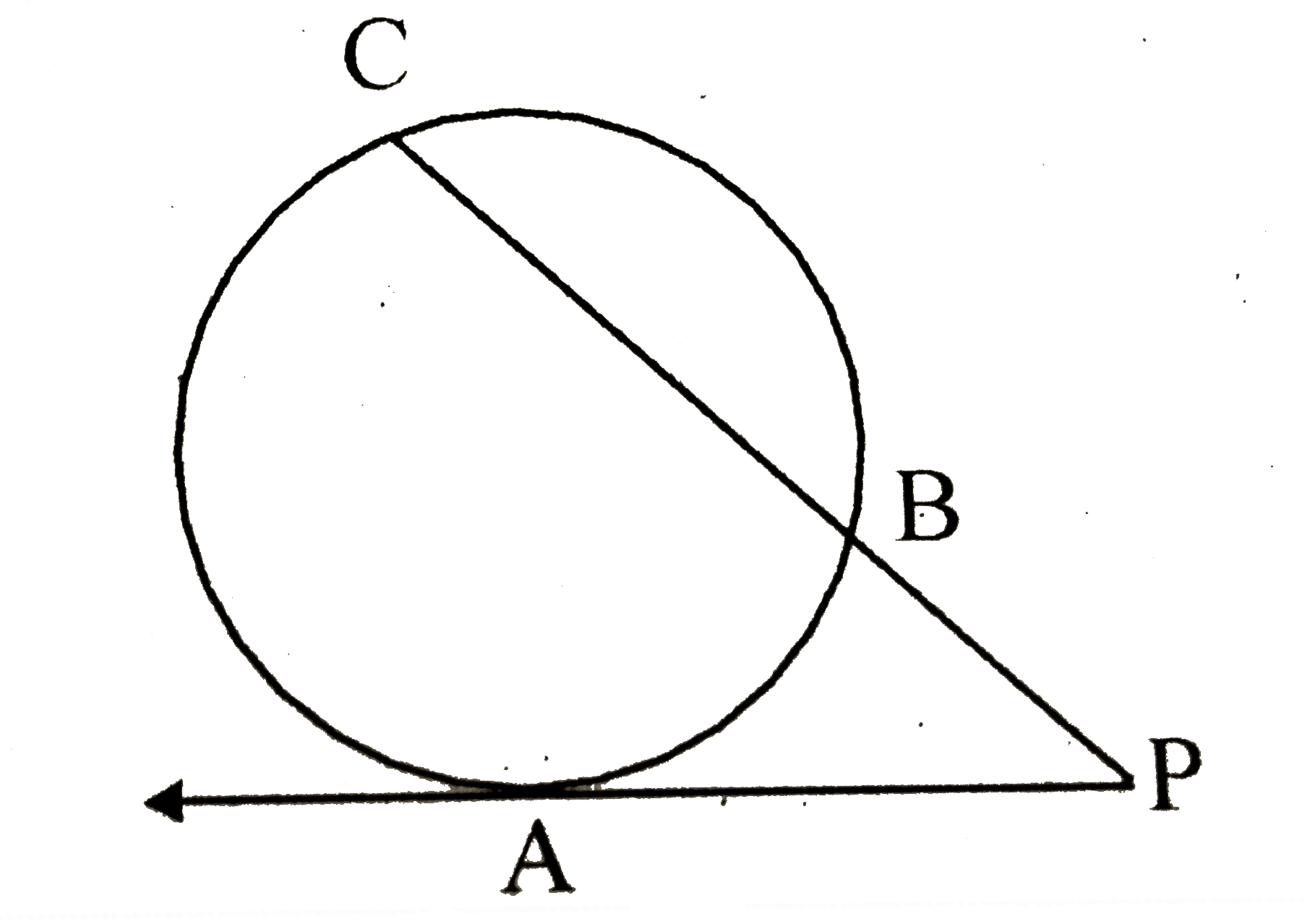
In the figure, a tangent segment PA touches the circle at point A and secant PBC intersects the circle at points B and C. If AP=15 cm and BP=10, then find BC.
The correct Answer is:BC=12.5
Step by step video & image solution for In the figure, a tangent segment PA touches the circle at point A and secant PBC intersects the circle at points B and C. If AP=15 cm and BP=10, then find BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.1
9 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.2
8 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.5
8 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
Knowledge Check
The radius of two concentric circles are 17cm and 10cm. A straight line ABCD intersects the larger circle at the point A and D and intersects the smaller circle at the points B and C. If BC = 12 cm, then the length of AD (in cm) is :
A20B24C30D34In the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at N and R. PQ=15cm,PR=25cm, find PN:
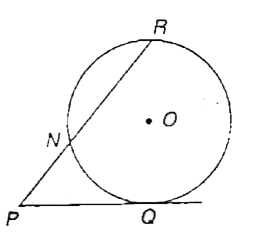 A15 cmB10 cmC9 cmD6 cm
A15 cmB10 cmC9 cmD6 cm
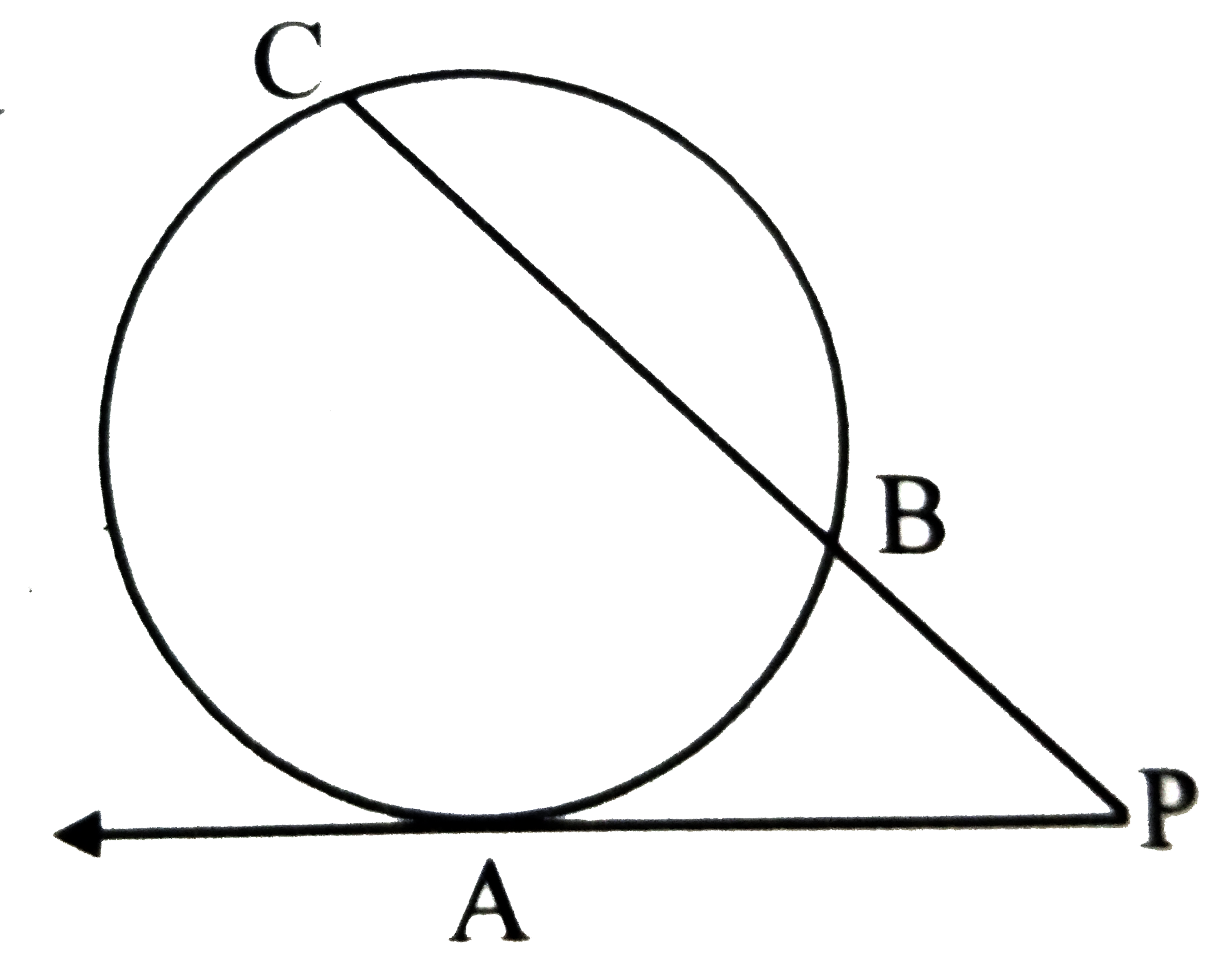
In the following figure, a tangent segment PA touching a circle in A and a secant PBC are shown. If AP=12,BP=9, find BC.
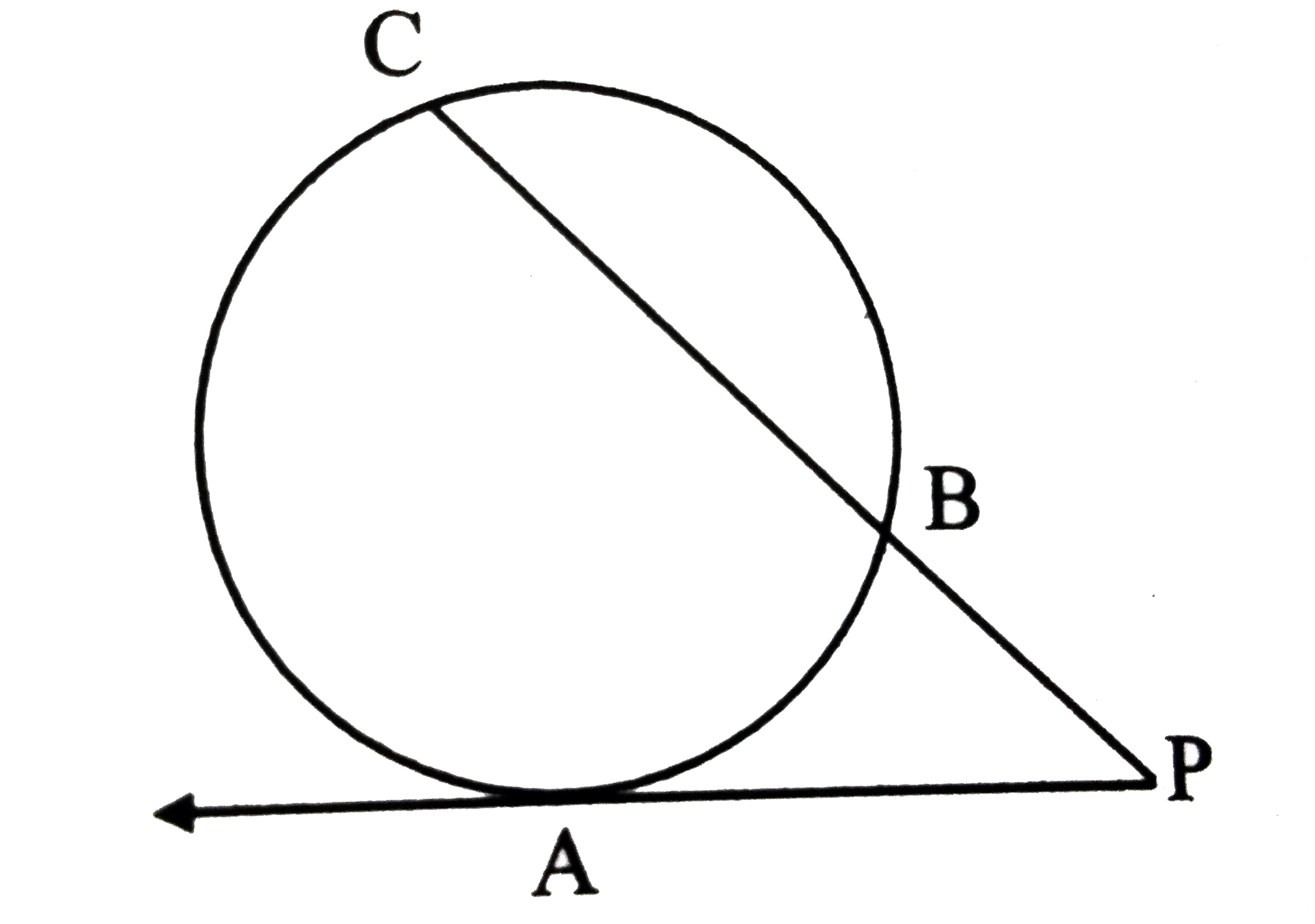
View SolutionIn the following figure, a tangent segment PA touching a circle in A and a secant PBC are shown. If AP = 12, BP = 9, find BC.
View SolutionIn the given figure, a tangent segment PA touching a circle in A and a secant PBC are shown If AP=15 cm and BP=10cm , find the Length of PC.
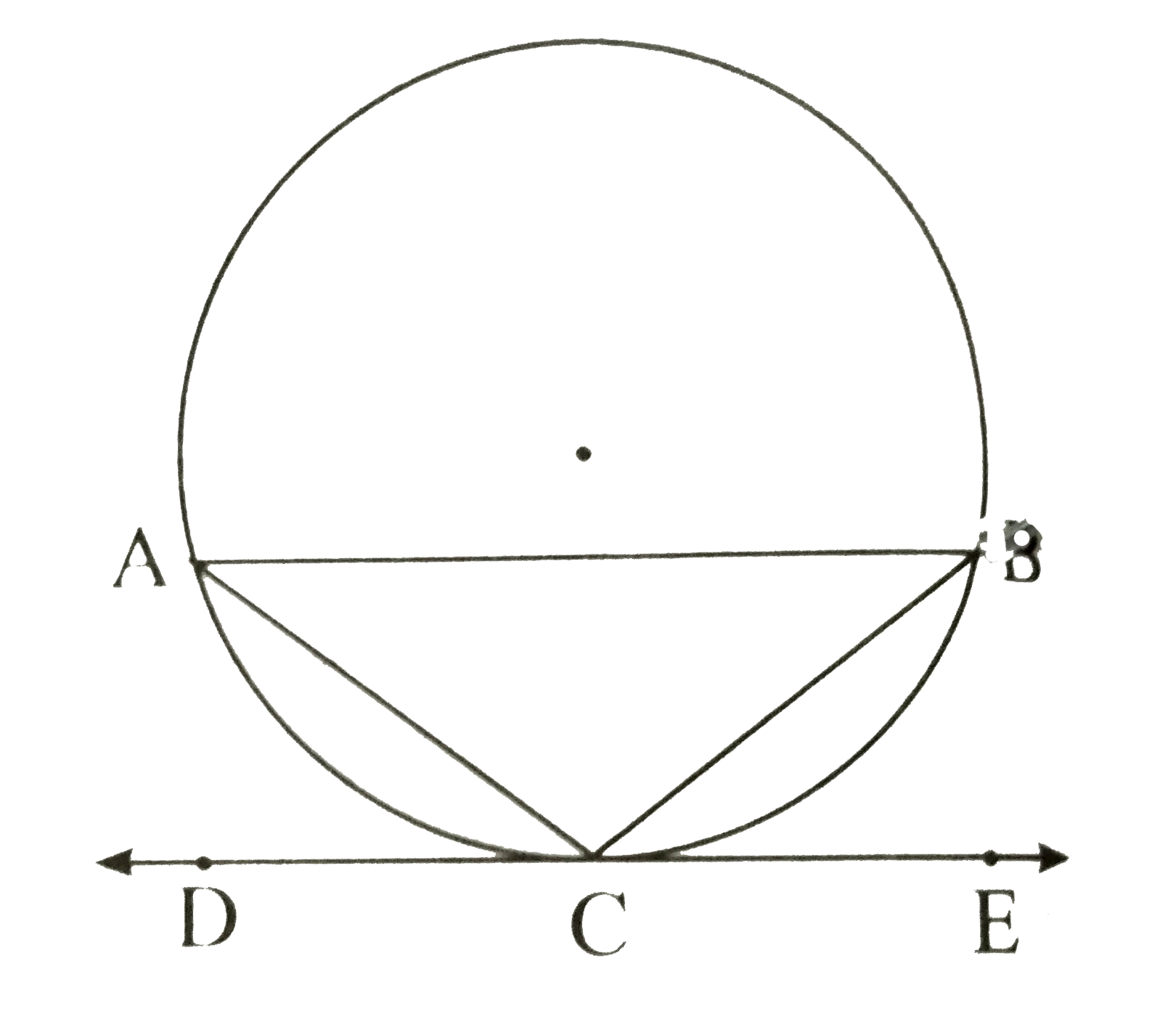
View SolutionIn the figure, chord AB∣∣ tangent DE. Tangent DE touches the circle at point C then prove AC = BC.
View SolutionTangent Secant Theorem
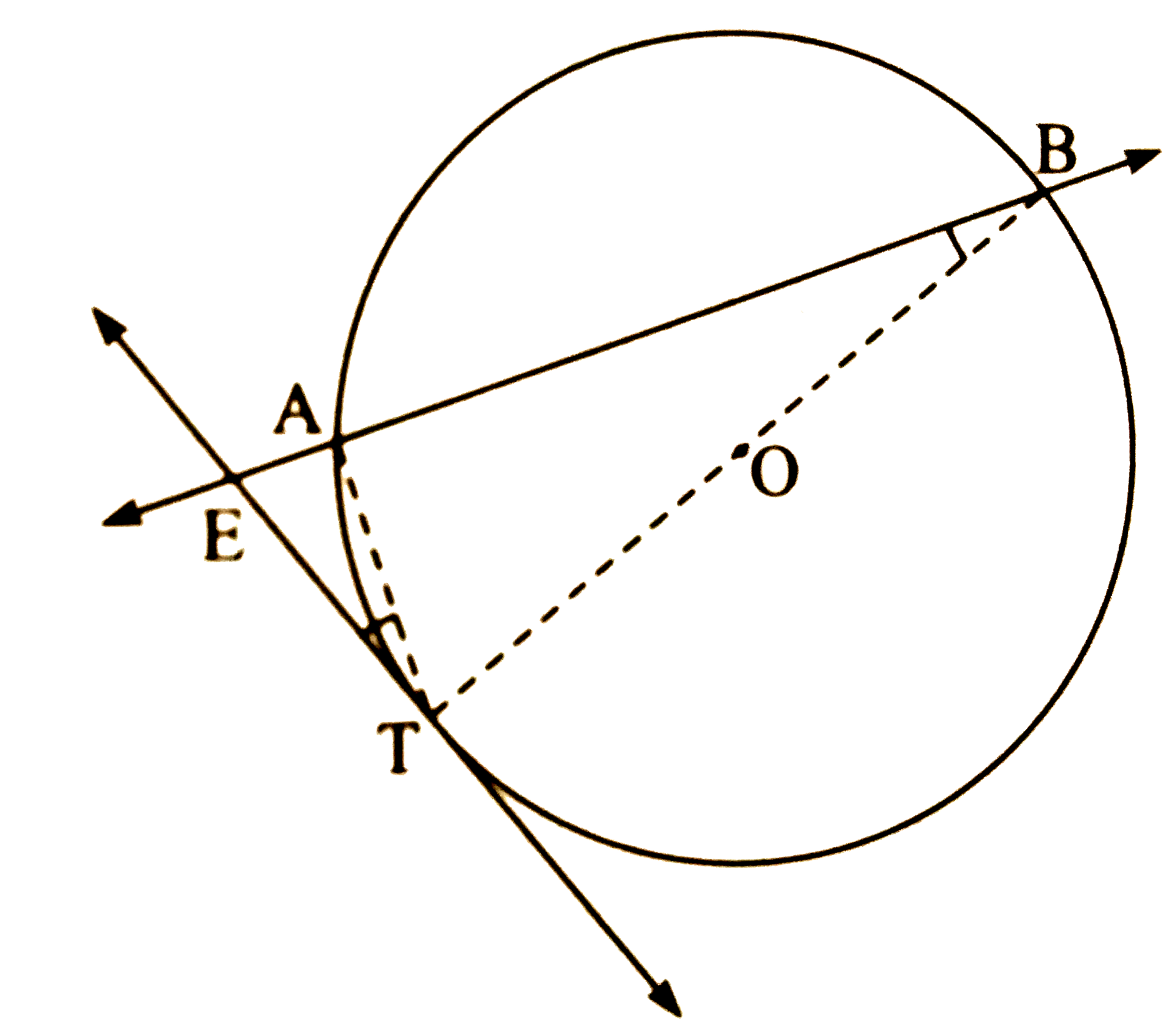
Point E is in the exterior of a circle. A secant through E intersects the circle at points A and B, and a tangent through E touches the circle at point T, then EA×EB=ET2.
Given : (1) A circle with centre O
(2) Tangent ET touches the circle at pointT
(3) Secant EAB intersects the circle at points A and B .
To prove : EA×EB=ET2
View SolutionAs shown in the figure, AP is tangent to the circle at point A. Secant through P intersects chord AY in point X, such that AP=PX=XY. If PQ = 1, QZ =8. Then find AX

View Solution