In the adjoining figure, two points A and B lie on the same side of a line XY. If AD⊥XY,BE⊥XY and C is the midpoint of AB, prove that CD = CE.
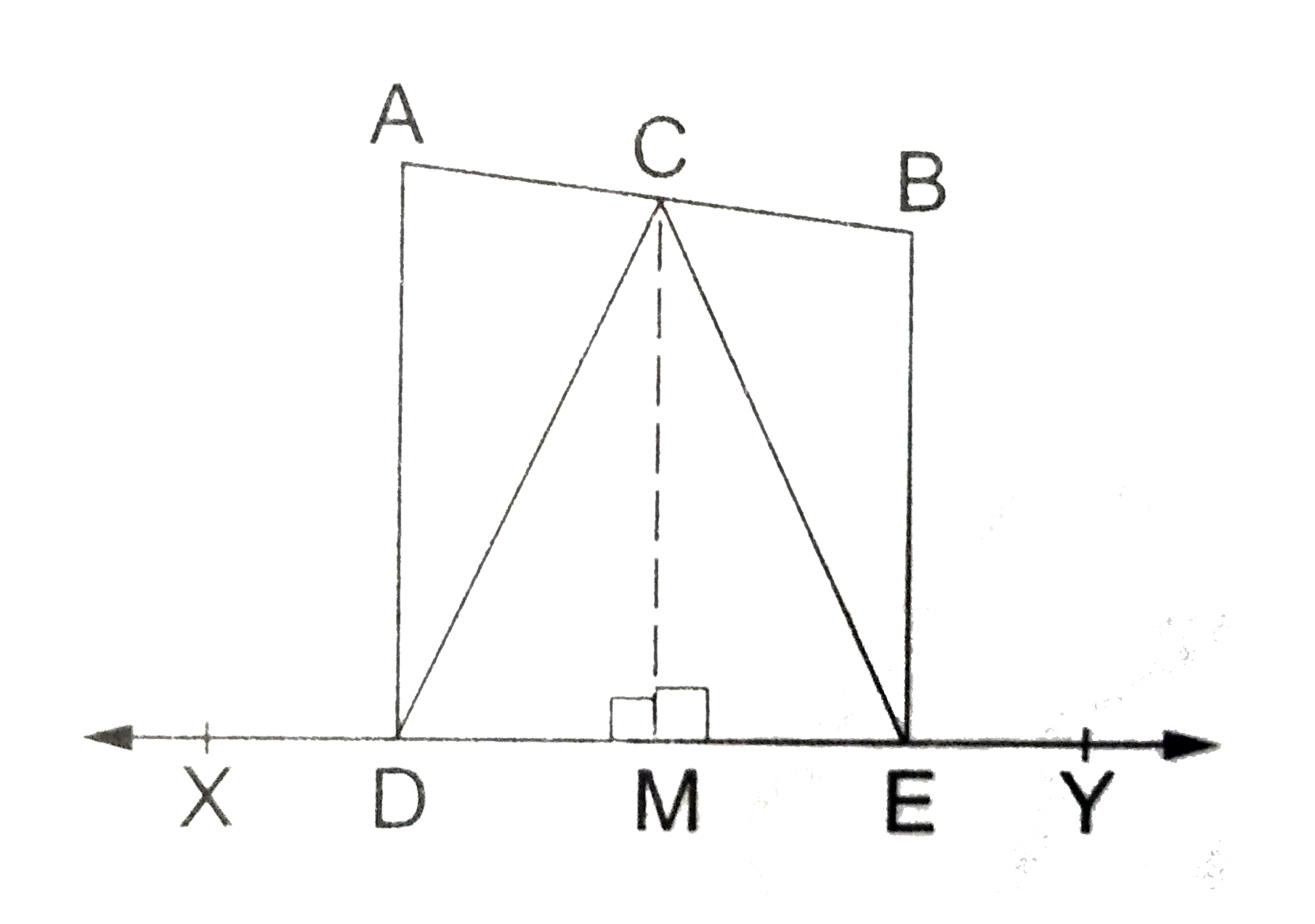
Draw CM⊥XY.
Now, AD⊥XY,CM⊥XYandBE⊥XY⇒AD||CM||BE.
Thus, AD, CM, BE are three parallel lines, cut by the transversal ACB at A, C and B respectively such that AC = CB.
These lines AD, CM, BE are also cut by the transversal XY at D, M and E respectively.
∴DM=ME (by intercept theorem).
Now, in △CDM and CEM, we have
DM=ME (proved), CM=CM (common),
∠CMD=∠CME=90∘.
∴△CDM≅△CEM.
Hence, CD=CE (c.p.c.t.).
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B
27 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
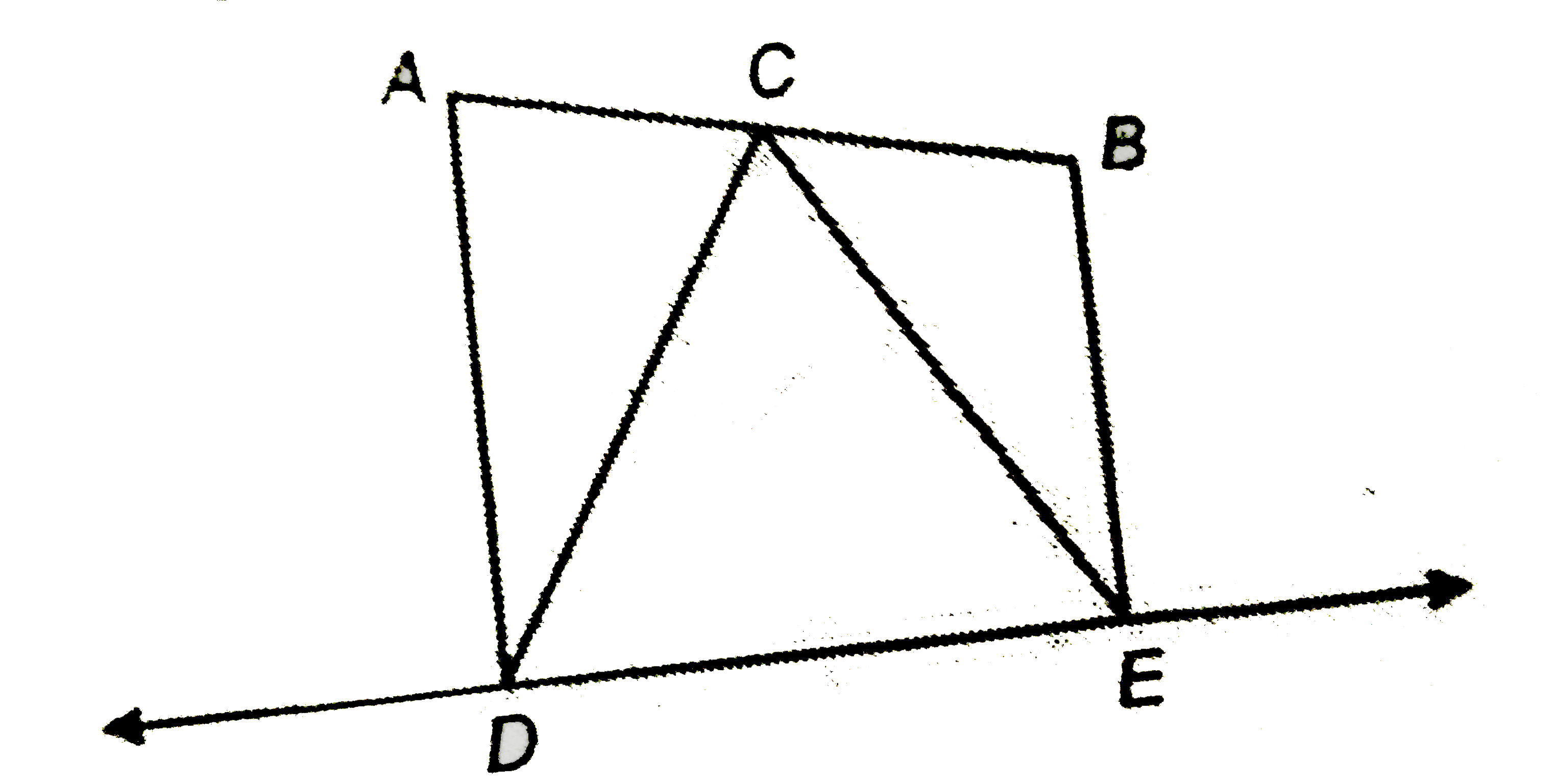
In the adjoining figure, two points A and B lie on the same side of a line 'l'. C is the mid-point of AB. If AD ⊥landBE⊥l, then prove that CD = CE.
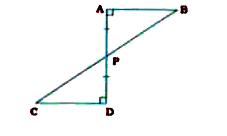
View SolutionIn the given figure, AB and DC are both perpendicular to line segment AD. BC intersects AD at P and P is the midpoint of AD. Prove that, ( 1 ) AB = CD ( 2 ) P is the midpoint of BC.
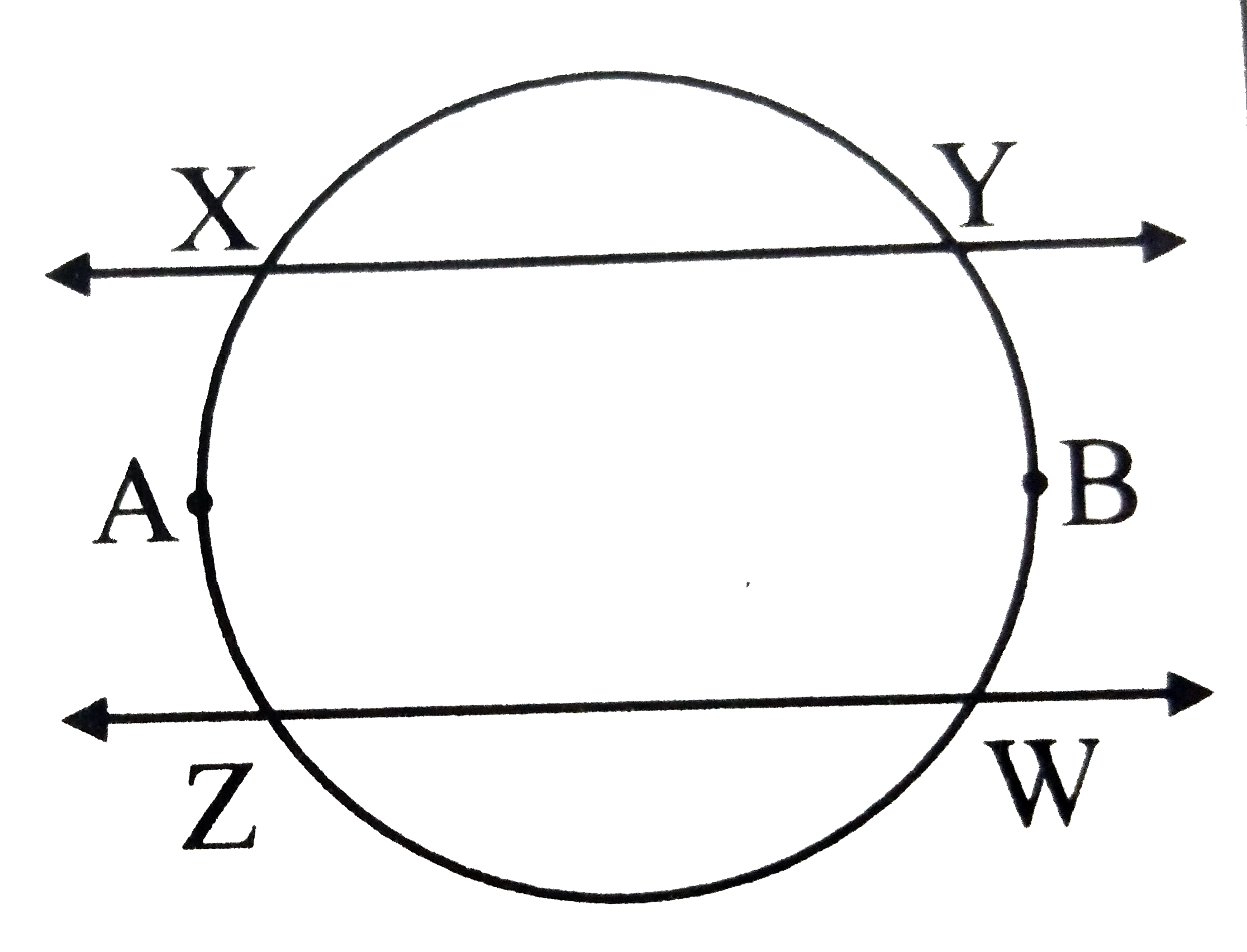
View SolutionIn the adjoining figure, m (arc XAZ)=m(arc YBW). Prove that : XY∣∣ZW
View SolutionIn the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.

View SolutionIn the adjoining figure, AP⊥BC,AD||BC, then find A(ΔABC):A(ΔBCD).

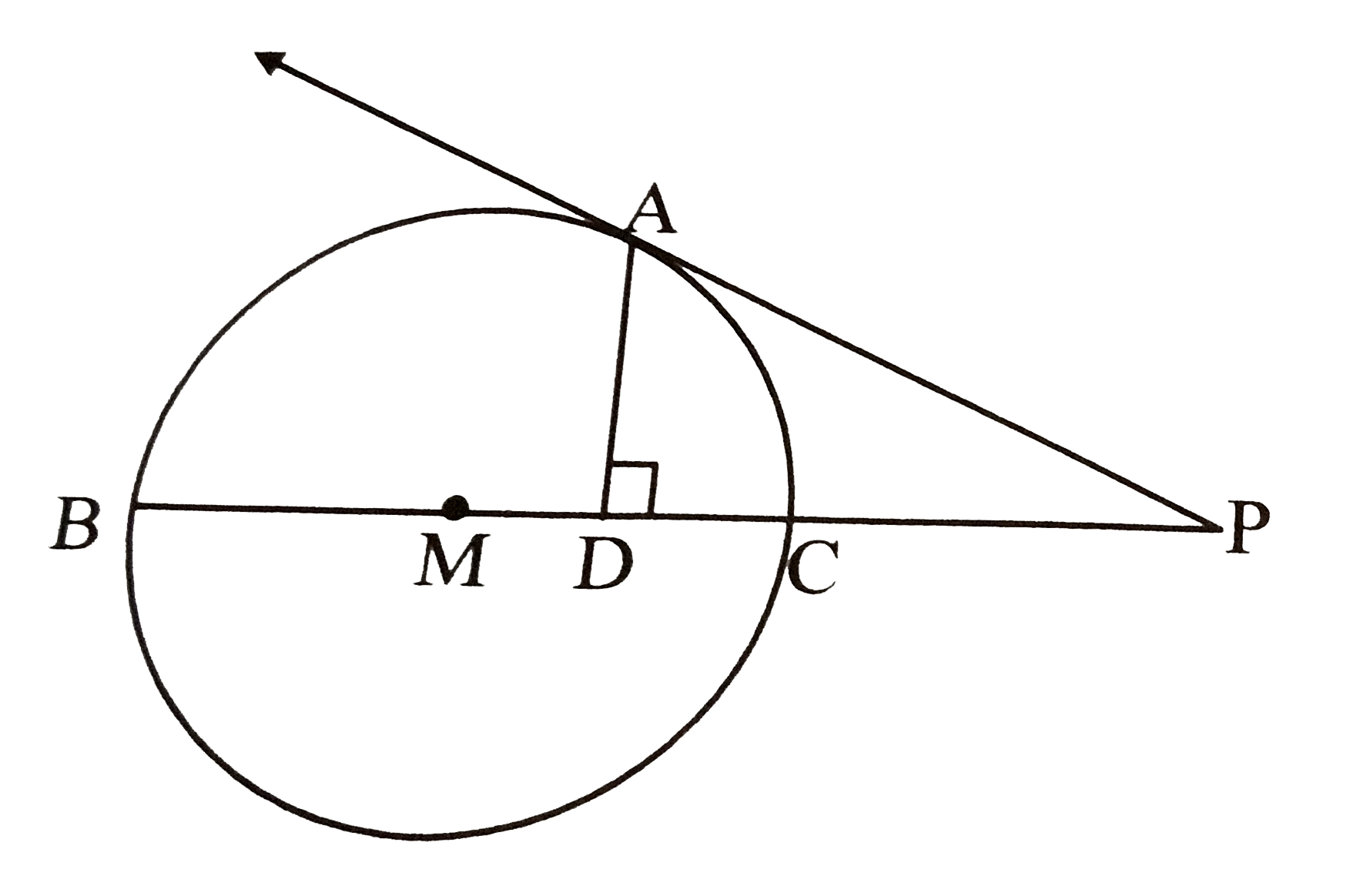
View SolutionIn the adjoining figure, BC is a diameter of the circle with centre M. PA is a tangent at A from P, which is a point on line BC. AD ⊥ BC
prove that DP2=BP×CP−BD×CD
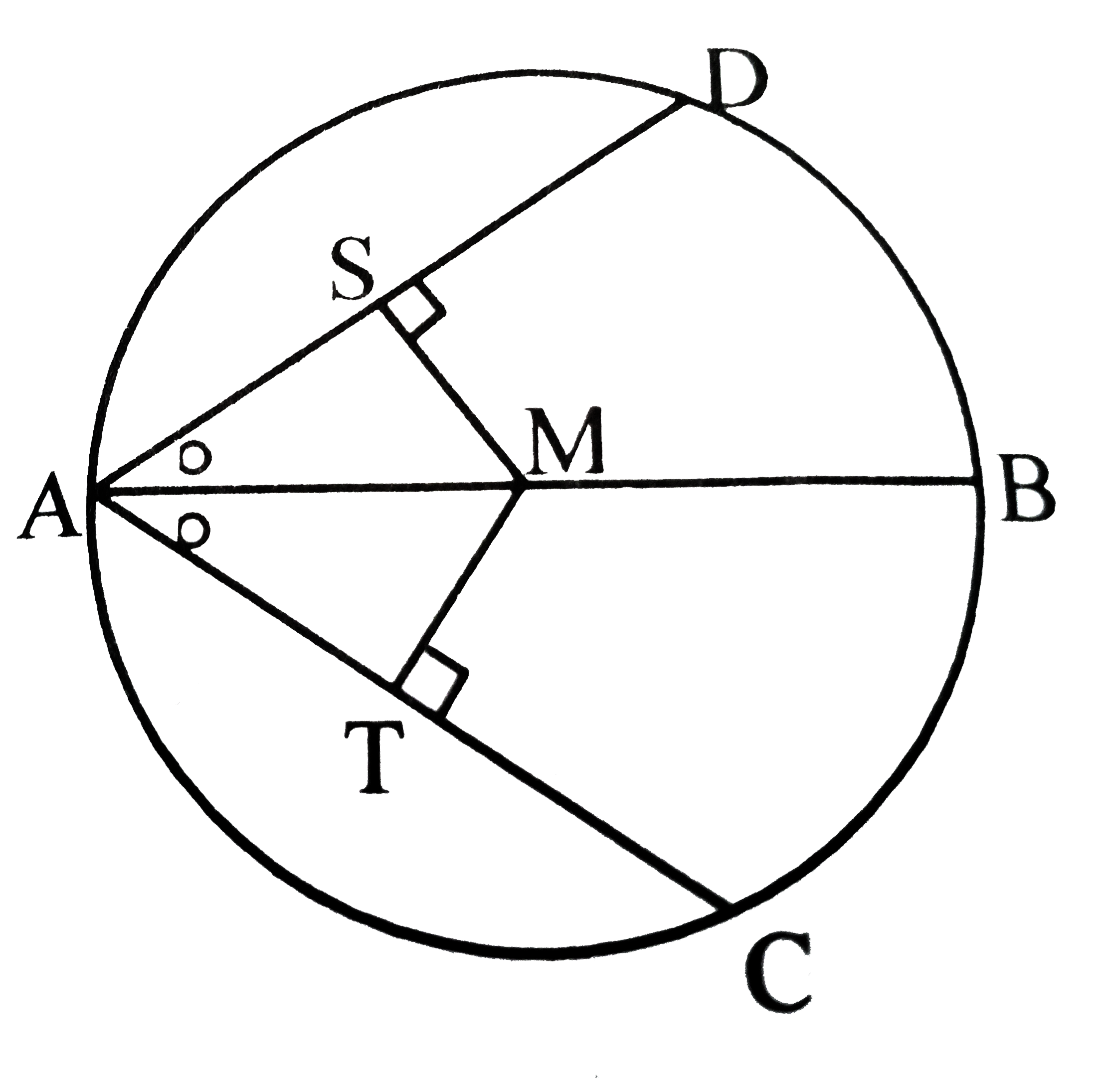
View SolutionIn the adjoining figure, M is the centre of the circle and seg AB is a diameter. Seg MS⊥ chord AD, seg MT ⊥ chord AC, ∠DAB≅∠CAB.
Prove that : chord AD≅ chord AC.
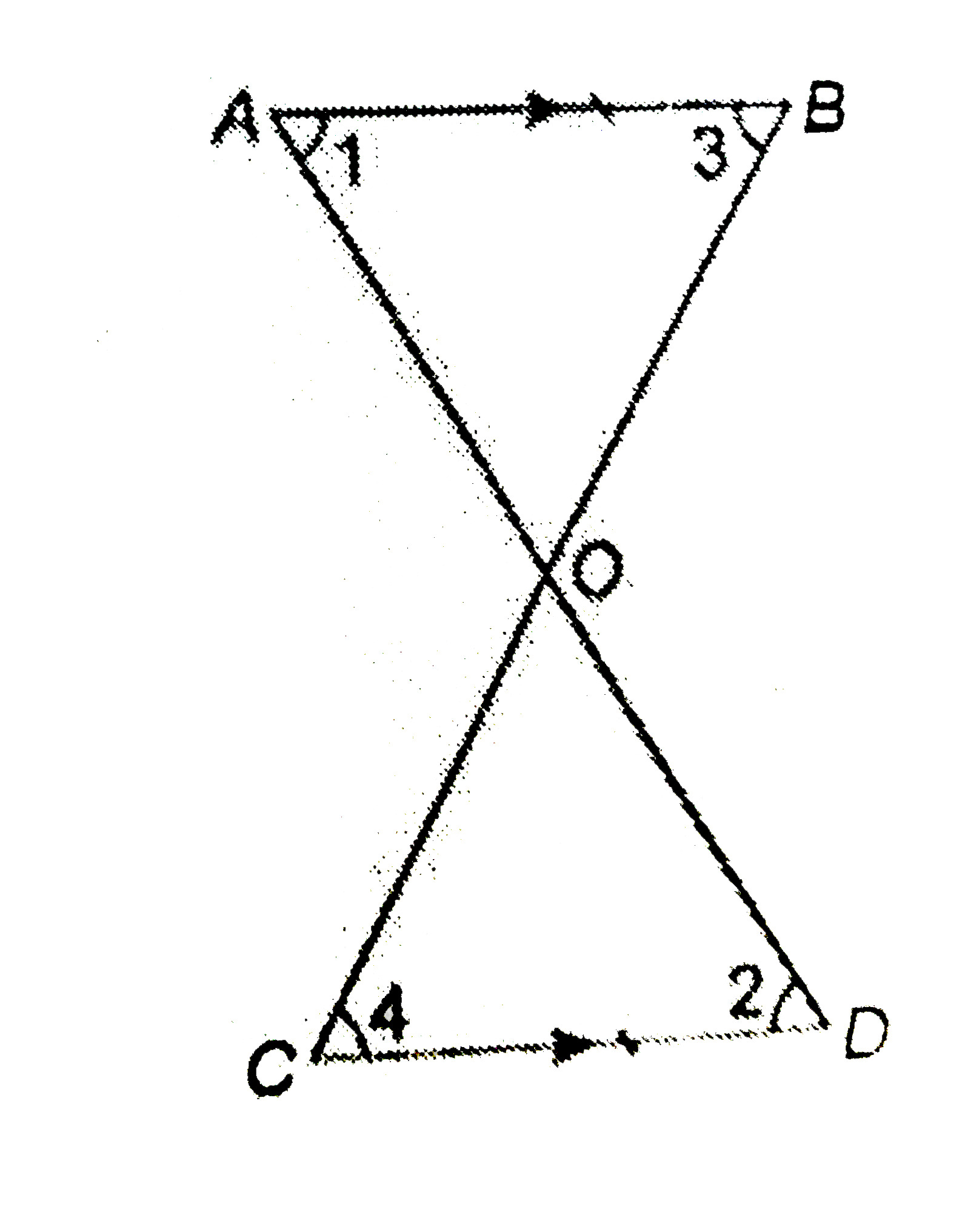
View SolutionIn the adjoining figure, AB = CD and AB||CD prove that
(i) ΔAOB≅ΔDOC
(ii) AD and BC bisect each other at the point O.
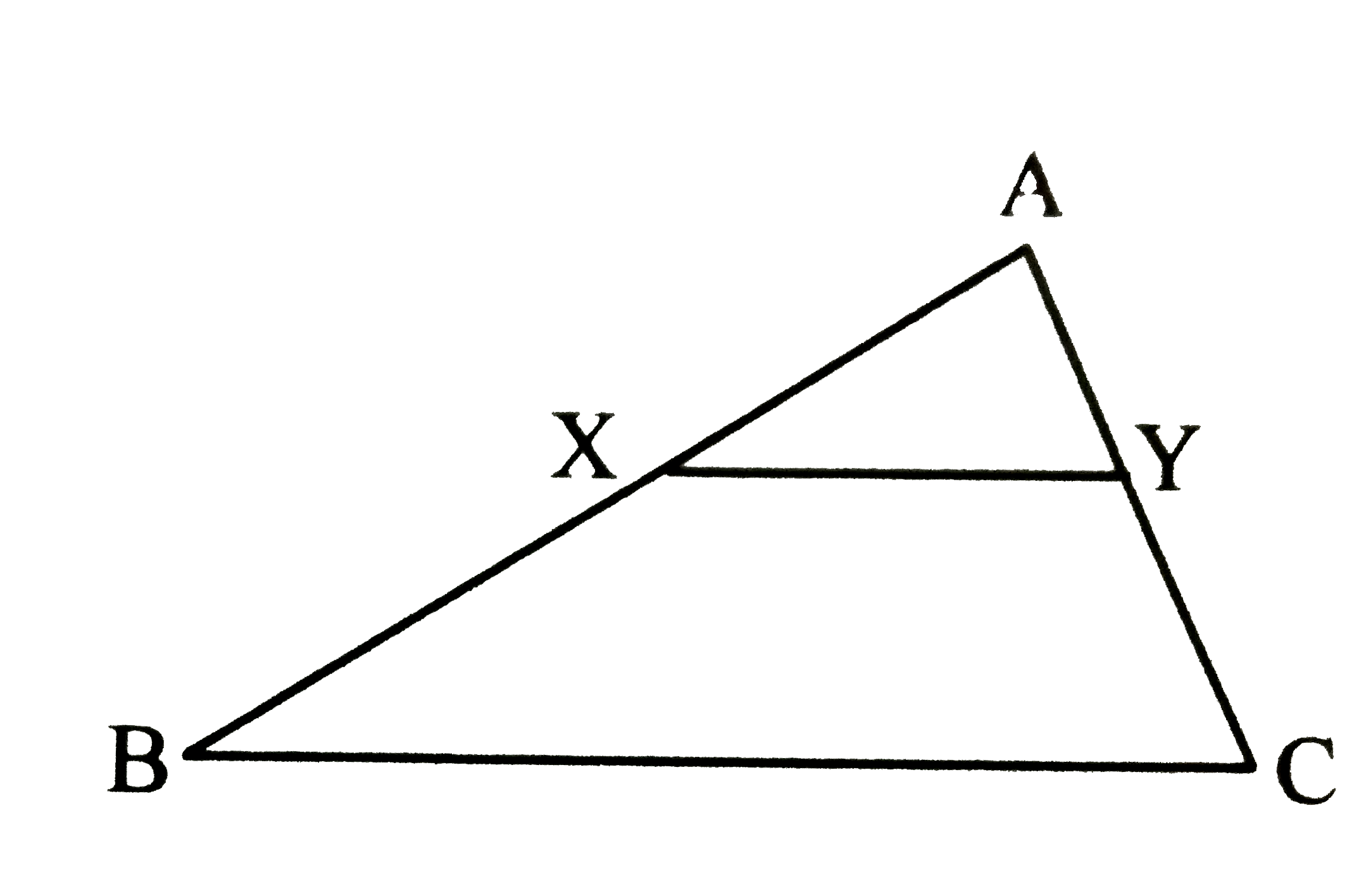
View SolutionIn the adjoining figure, seg XY ||seg BC, then which of the following statements is true?
View SolutionIn the given figure, E is a point on side CB produced of an isosceles ΔABC with AB=AC.. If AD⊥BCandEF⊥AC, prove tha ΔABD~ΔECF
View Solution
