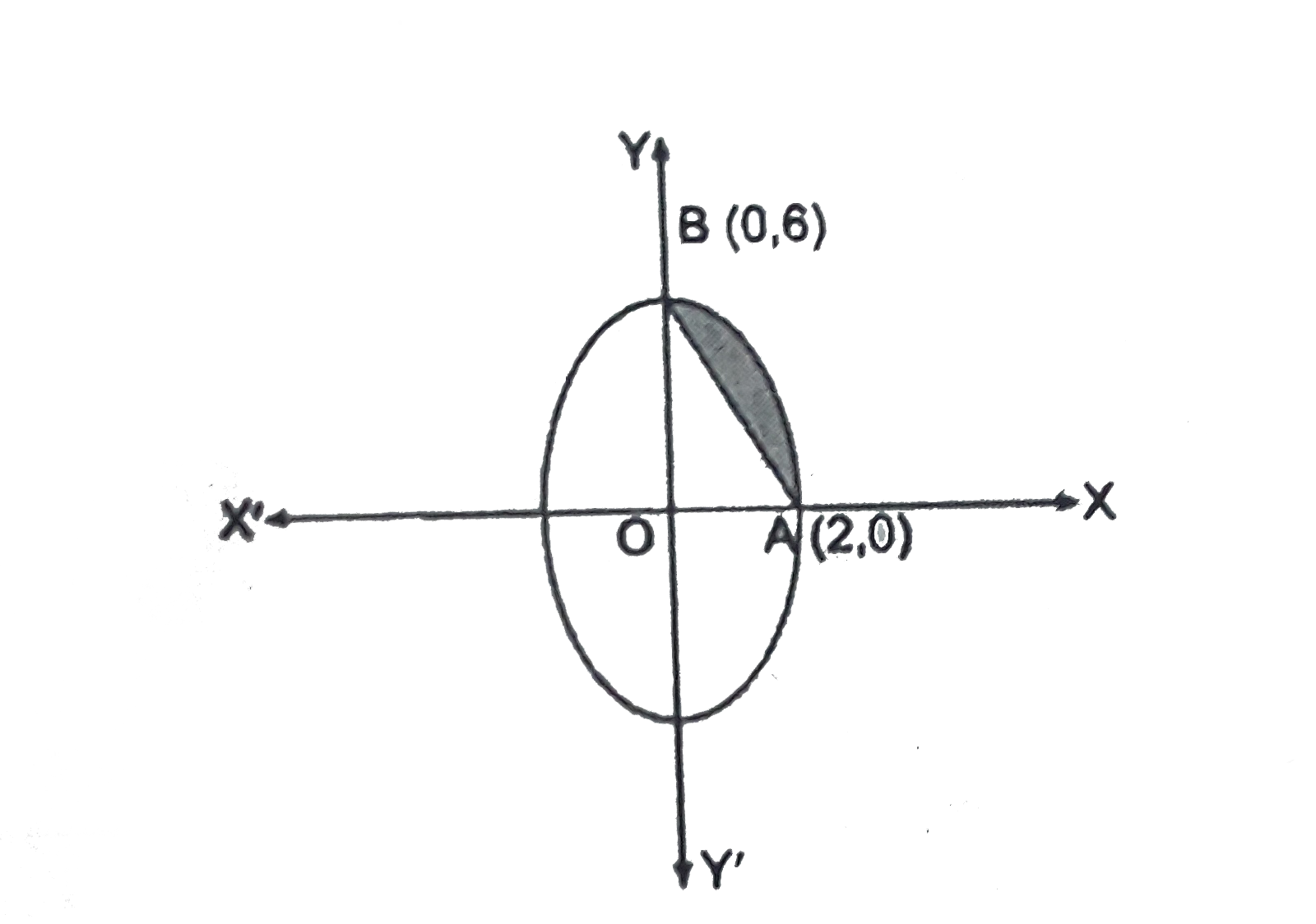
In the adjoining, $O A B O$ is the region of the ellipse $9 x^{2} + y^{2} = 36$ which lies in first quadrant. If $O A = 2, O B = 6,$ then find the area of the region bounded by chord AB and arc AB.

A

$(3 π - 8) s q .$ units.

B

$(3 π - 7) s q .$ units.

C

$(3 π - 6) s q .$ units.

D

$(3 π - 9) s q .$ units.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Equation of AB
$y - 0 = \frac{6 - 0}{0 - 2} (x - 2)$
$\Rightarrow y = - 3 x + 6$
Required area
$= \int_{0}^{2} 3 \sqrt{4 - x^{2}} d x - \int_{0}^{2} (- 3 x + 6) d x$
$= 3 {[\frac{x}{2} \sqrt{4 - x^{2}} + \frac{4}{2} {sin}^{- 1} \frac{x}{2}]}_{0}^{2} - {[\frac{- 3 x^{2}}{2} + 6 x]}_{0}^{2}$
$= 3 [(0 + 2 {sin}^{- 1} 1) - (0 + 0)] - [(- 6 + 12) - (0 + 0)]$
$= (3 π - 6) s q .$ units.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the adjoining, $O A B O$ is the region of the ellipse $9 x^{2} + y^{2} = 36$ which lies in first quadrant. If $O A = 2, O B = 6,$ then find the area of the region bounded by chord AB and arc AB.

A $(3 π - 8) s q .$ units.
B $(3 π - 7) s q .$ units.
C $(3 π - 6) s q .$ units.
D $(3 π - 9) s q .$ units.
Question 2 - Select One
The area of region bounded by $y = | x - 1 | and y = 1$ is
A1
B2
C $1 / 2$
DNone
Question 3 - Select One
The area of the region bounded by $y = x^{2}$ and $y = - x^{2} + 2$ is
A $\frac{5}{3}$
B $\frac{4}{3}$
C $\frac{8}{3}$
D1

NAGEEN PRAKASHAN-APPLICATIONS OF INTEGRALS-Miscellaneous Exercise

Home
Ask Doubt
Profile