In the figure, AB and CD are two chords of a circle, interacting each other at a point E. Prove that ∠AEC = 1/2(angle subtended by arc CXA. at the centre + angle subtended by arc DYB at the centre).

Text Solution
Verified by Experts

Given In a figure, two chords AB and CD intersecting each other at point E.
To prove ∠AEC=12
[angle subtended by arc C×A at centre + angle subtended by arc DYB at the centre]
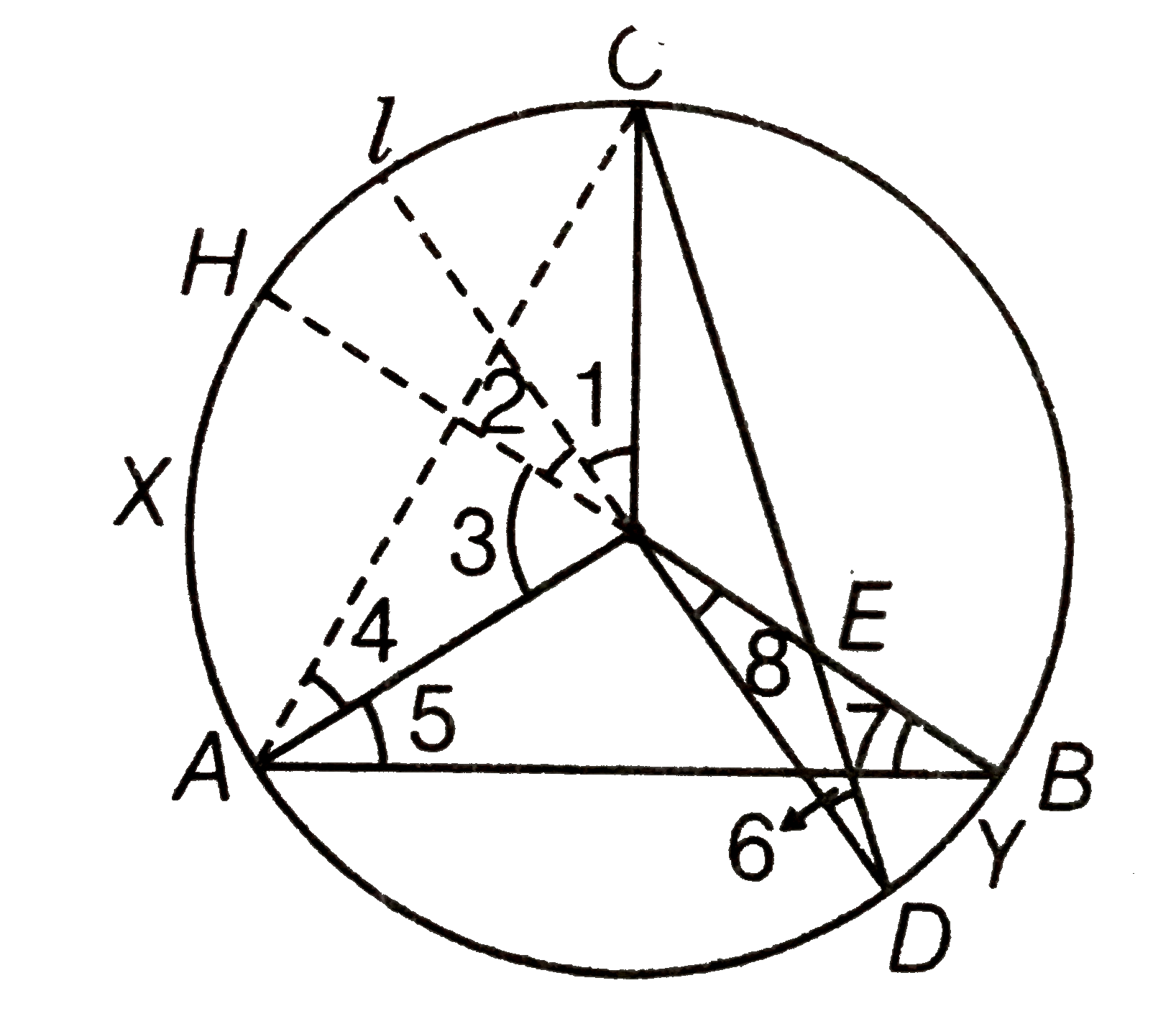
ocr_image
Construction Extend the line DO and BO at the points l and H on the circle. Also, join AC.
Proof We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
∴∠1=2∠6 ...(i)
and ∠3=2∠7 ....(ii)
In ΔAOC,OC=OA [ both are the radius of circle]
∠OCA=∠4 [angles opposite to equal sides arc equal]
Also, ∠OCA+∠OCA+∠4=180∘
[by angle sum property of triangle]
⇒∠AOC+∠4+∠4=180∘
⇒∠AOC=180∘−2∠4 ...(iii)
Now, in ΔAEC,∠AEC+∠ECA+∠CAE=180∘
[by angle property sum of a triangle]
⇒∠AEC=180∘−(∠ECA+∠CAE)
⇒∠AEC=180∘−[(∠ECO+∠OCA)+∠CAO+∠OAE]
=180∘−(∠6+∠4+∠4+∠5)
[in ΔOCD,∠6=∠ECO angles opposite to equal sides are equal]
=180∘−(2∠4+∠5+∠6)
=180∘−(180∘−∠AOC+∠7+∠6)
[from Eq. (iii) and in ΔAOB,∠5=∠7, as (angles opposite to equal sides are equal)]
∠AOC−∠32−∠12 [from Eqs. (i) and (ii)]
=∠AOC−∠12−∠22−∠32−∠22[adding and subtracting ∠22]
=∠AOC−12(∠1+∠2+∠3)+∠82[∵∠2=∠8 (vertically opposite angles)]
=∠AOC−∠AOC2+∠DOB2
⇒∠AEC=12(∠AOC+∠DOB)
12 [angle subtended by arc CXA at the centre + angle subtended by arc DYB at the centre]

Doubtnut Promotions Banner
|
Class 9MATHSCIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A, B and C are the three points on a circle such that ∠ABC=35∘and∠BAC=85∘. What is the angle (in degrees) subtended by arc AB at the centre of the circle?

    A60
    B90
    C135
    D120

  • If the chord of a circle is equal to the radius of the circle, then the angle subtended by the chord at a point on the minor arc is:

    A120∘
    B150∘
    C100∘
    D110∘