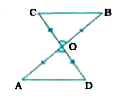
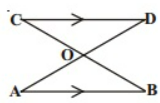
In the figure AB || CD, AD and BC intersect at o and O is mid-point of AD. Show that
(i) ΔAOB≅ΔDOCand(ii)OB=OC.
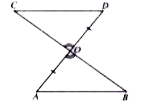
Step by step video & image solution for In the figure AB || CD, AD and BC intersect at o and O is mid-point of AD. Show that (i) DeltaAOB~=DeltaDOC and (ii) OB=OC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
In the given figure, AB||CDandO is the midpoint of AD.
Show that (i) ΔAOB≅ΔDOC.
(ii) O is the midpoint of BC.
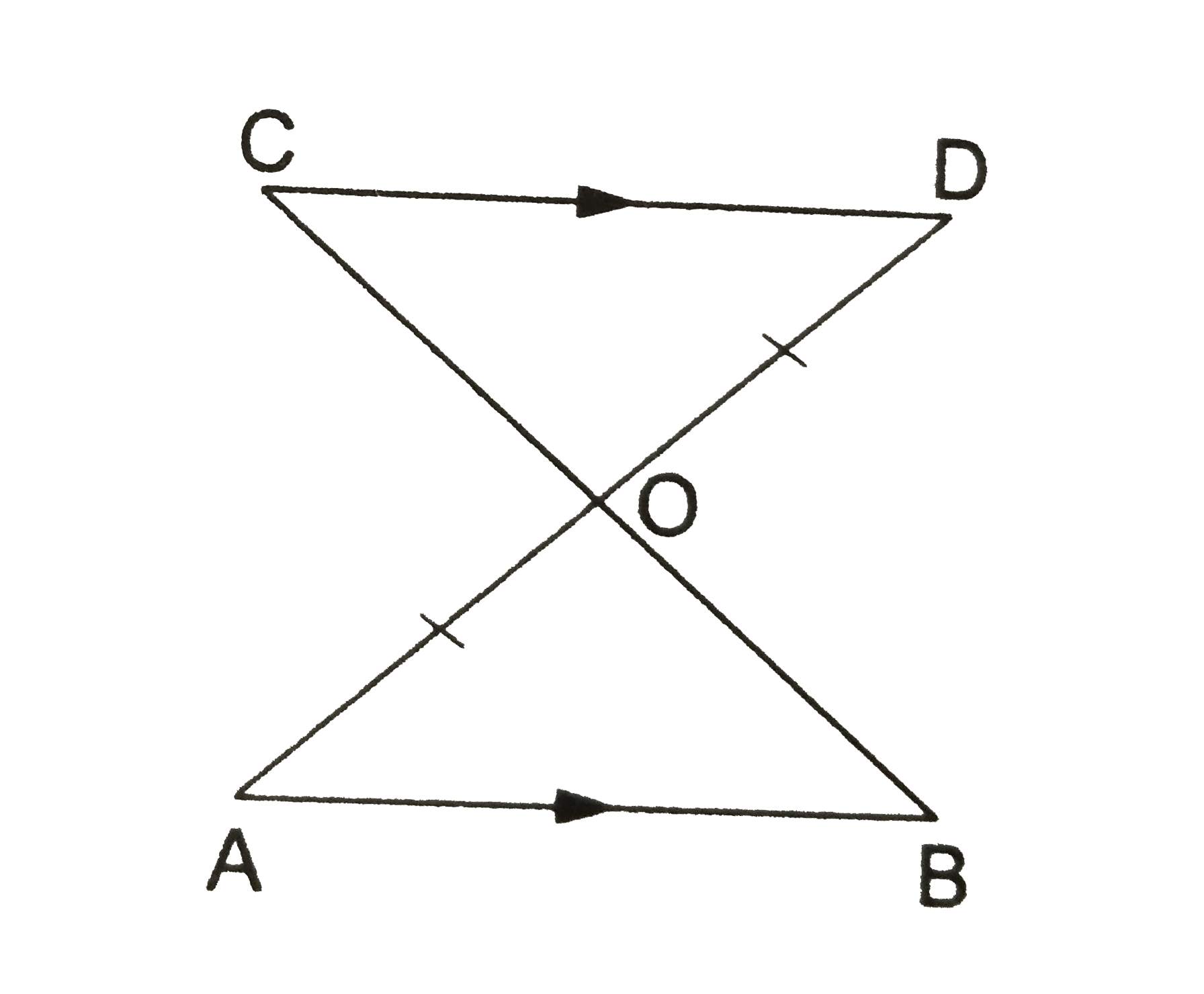 View Solution
View SolutionIn the figure if AB || CD and AD||BC, find ∠Aand∠D
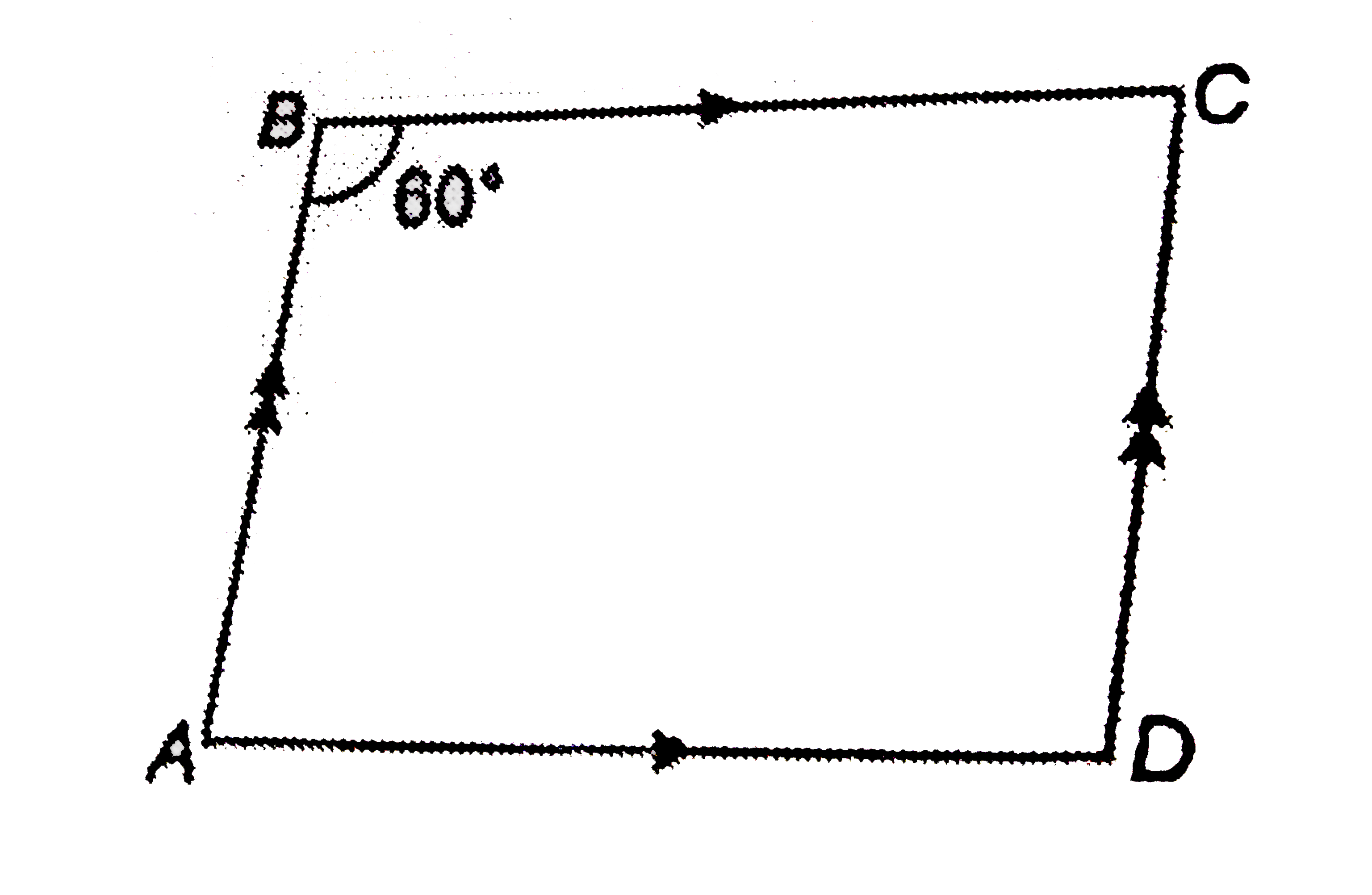 View Solution
View SolutionIn the give figure AB = BC, M is the mid point of AB and N is the mid point of BC, Show that AM = NC
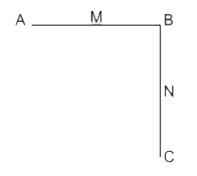 View Solution
View SolutionIn the given figure, OA = OB and OD = OC. Show that
(i) ΔAOD≅ΔBOC and (ii) AD∣∣BC
 View Solution
View SolutionLine-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see Fig. 7.15). Show that
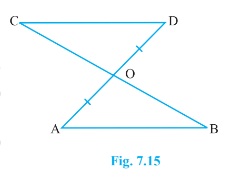
(i) ΔAOB≅ΔDOC
(ii) O is also the mid-point of BCView SolutionIn Figure, line segment AB is parallel to another line segment CD . O is the mid-point of AD . Show that: (i)AOB≅DOC (ii)O is also the mid-point of BC.
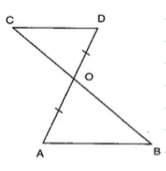 View Solution
View SolutionIn the given figure. AB∣CDandO is the midpoint of AD.
View SolutionIn the given figure, AD and BC are equal perpendicualrs to a line segment AB.
Show that CD bisects AB.
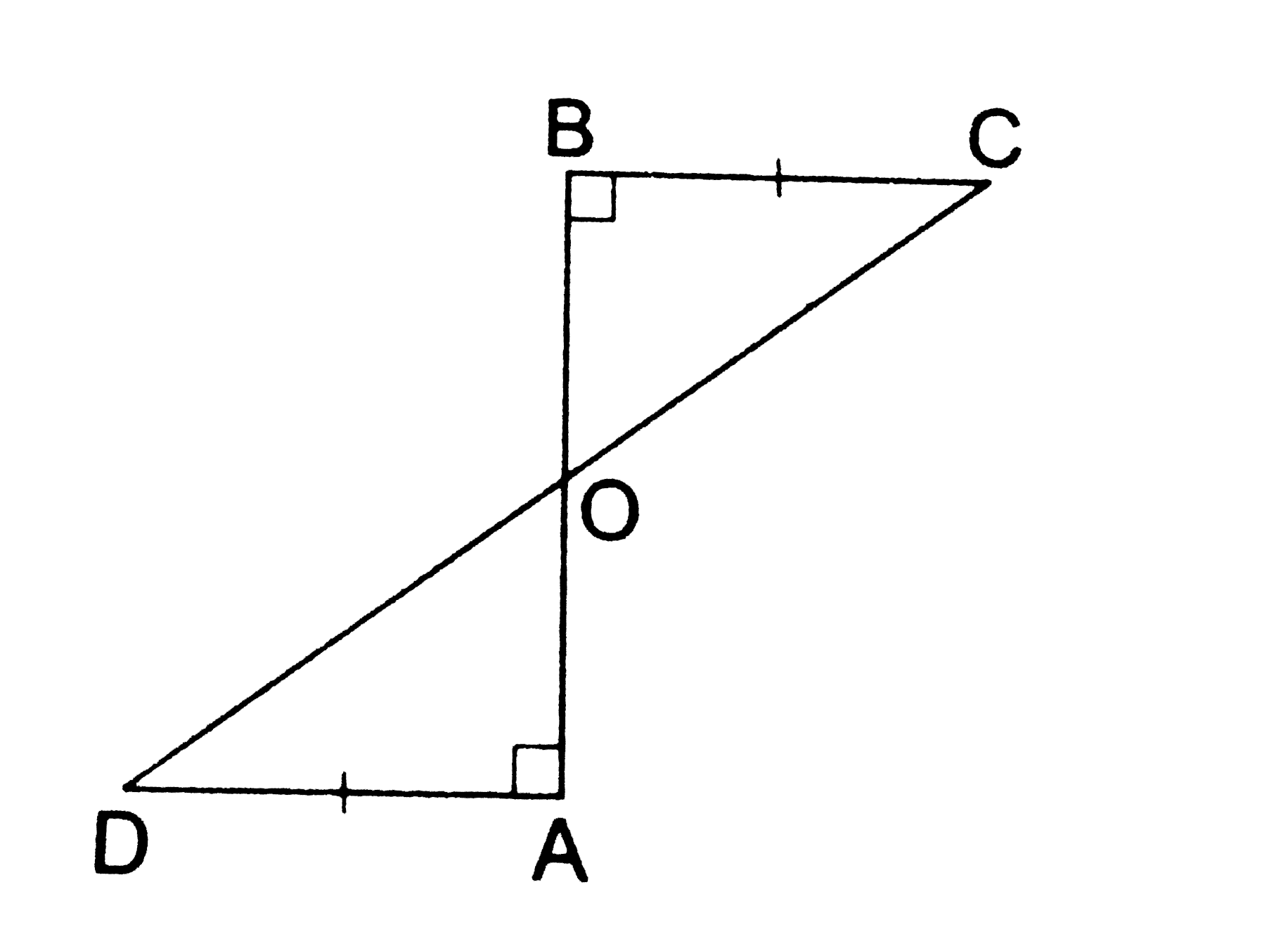 View Solution
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: AOB≅ DOC
 View Solution
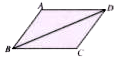
View SolutionIn quadrilateral ABCD, AB||CD and BC||AD. Show that
(i) ΔABD≅ΔCDB
 View Solution
View Solution
