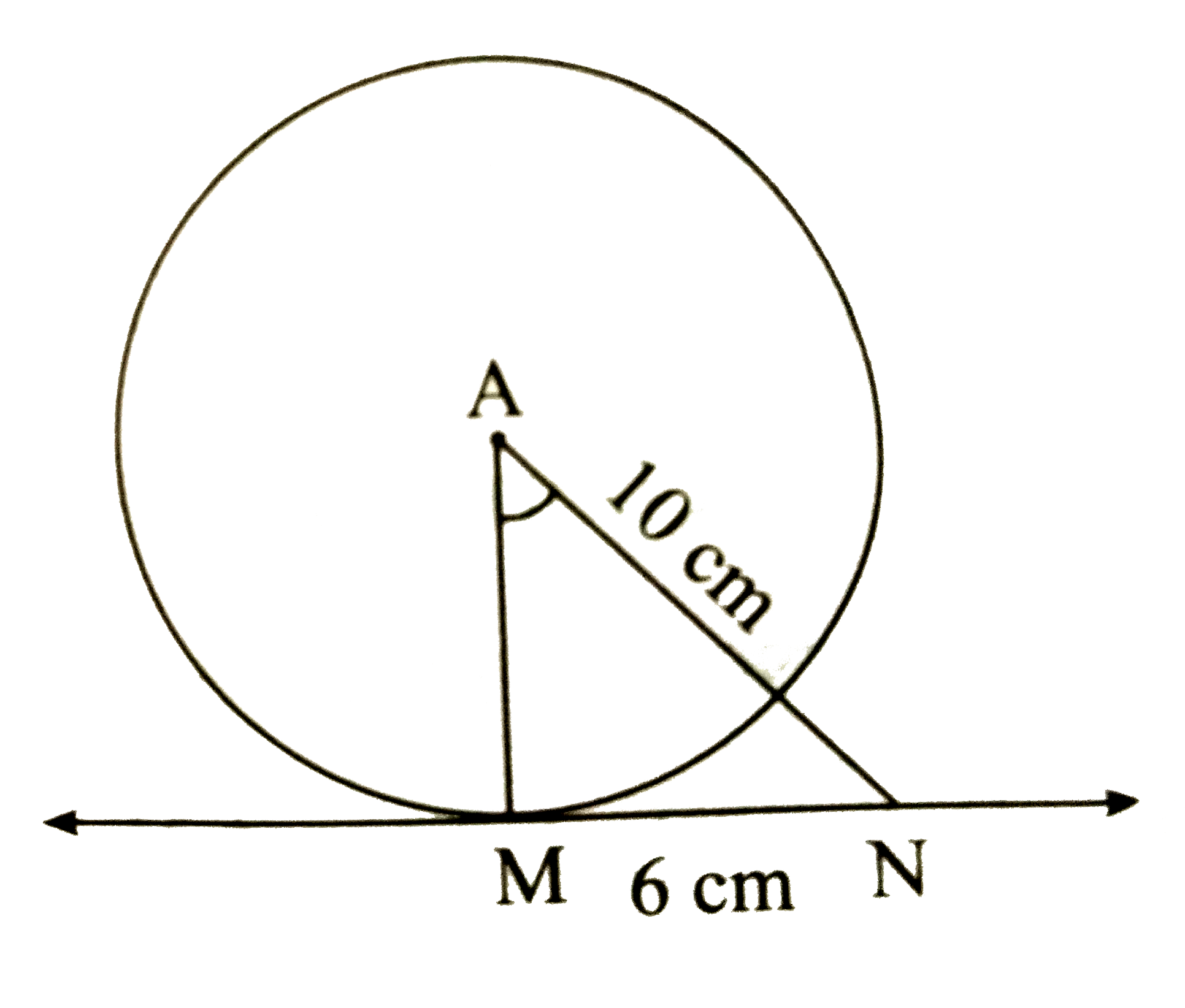In the figure, M is the centre of the circle and seg KL is a tangent segment. If MK=12,KL=6√3 then find,
(1) Radius of the circle,
(2) Measures of ∠K and ∠M.

In ΔMLK,
∠MLK=90∘ ….(Tangent theorem)
∴ by Pythagoras theorem,
MK2=ML2+LK2
∴122=ML2+(6√3)2
∴144=ML2+36×3
∴144=ML2+108
∴ML2=144−108
∴ML2=36
∴ML=6 ...(Takin quare roots of both the sides )
∴ radius of the circle = ML = 6 .
In ΔMLK,
ML=12MK
∴∠K=30∘ ...(By converse of 30∘−60∘−90∘ triangle theorem )
In ΔMLK,
∠M+∠K+∠L=180∘ ...(Sum of all angles of a triangle is 180∘0
∴∠M+30∘+90∘=180∘0
∴∠M+120∘=180∘
∴∠M=180∘−120∘
∴∠M=60∘
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.5 (1 mark each)7videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.110videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.3 (1 mark each)11videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure, O is the centre of a circle and AT is a tangent at point A. The measure of ∠BAT is:
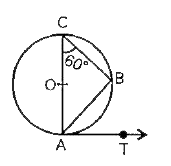 A30∘B60∘C75∘D105∘
A30∘B60∘C75∘D105∘
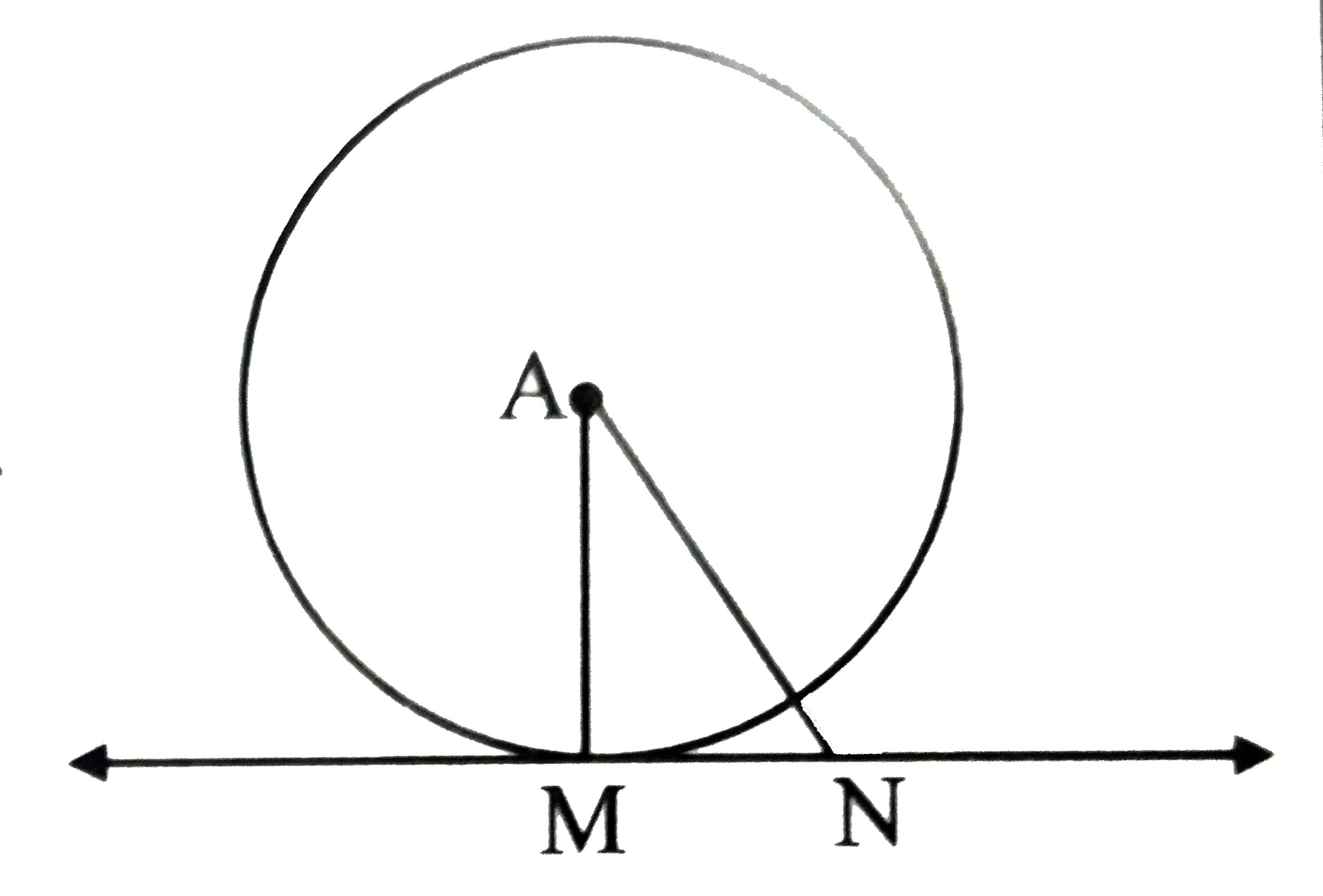
In the following figure, point ‘A’ is the centre of the circle. Line MN is tangent at point M. If AN = 12 cm and MN = 6 cm, determine the radius of the circle.
 View Solution
View SolutionIn the following figure ,Point A is the centre of the circle . Line MN is tangent at point M. IF AN=12cm and MN=6cm , determine the radius of the circle.
 View Solution
View SolutionIn the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
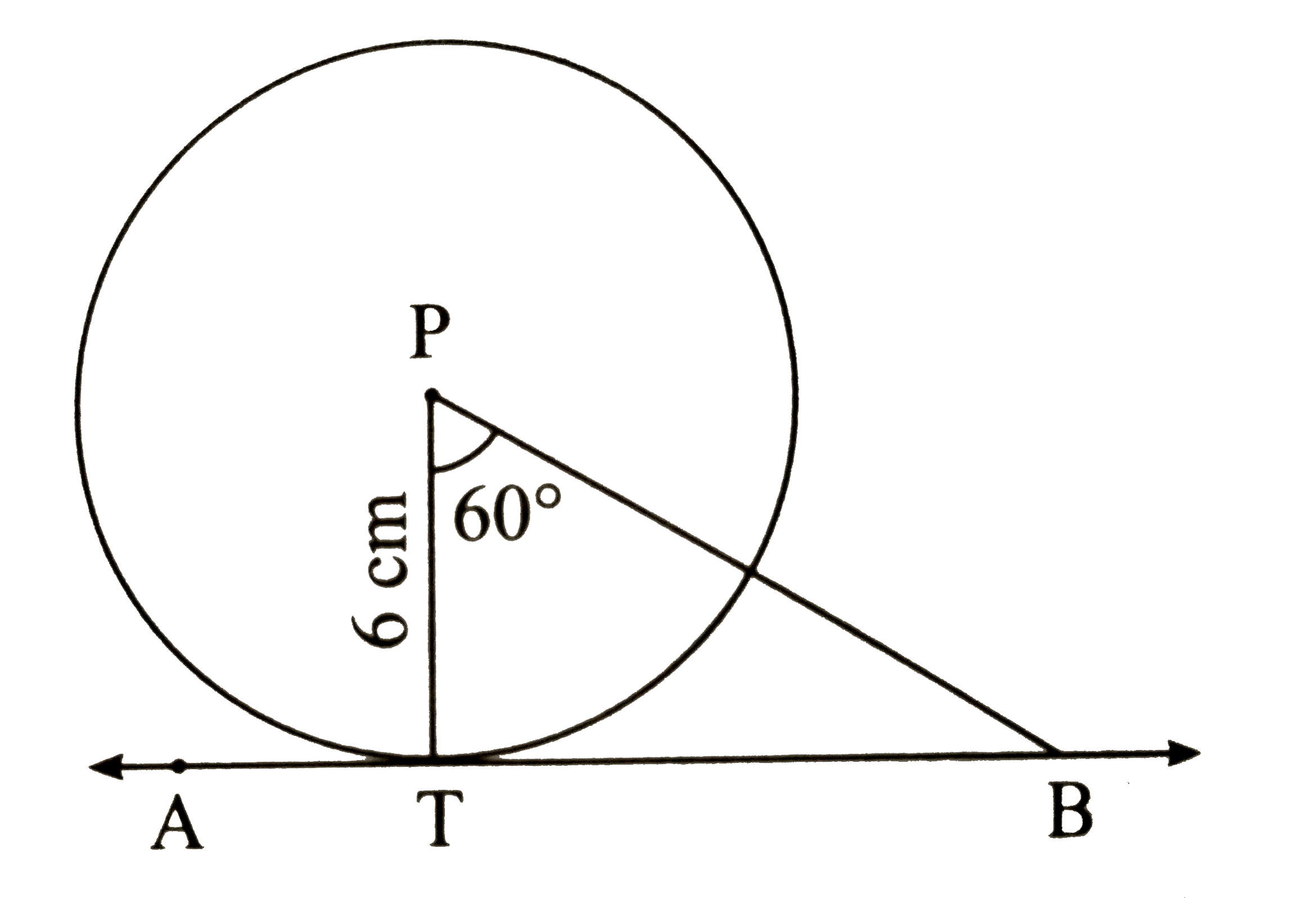 View Solution
View SolutionIn the given figure, P is the centre of the circle of radius 6 cm. Seg QR is a tangent at Q. If PR=12, find the area of the shaded region. (√3=1.73)
 View Solution
View SolutionIn the figure, O is the centre of the circle of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that, □ABOC is a square.
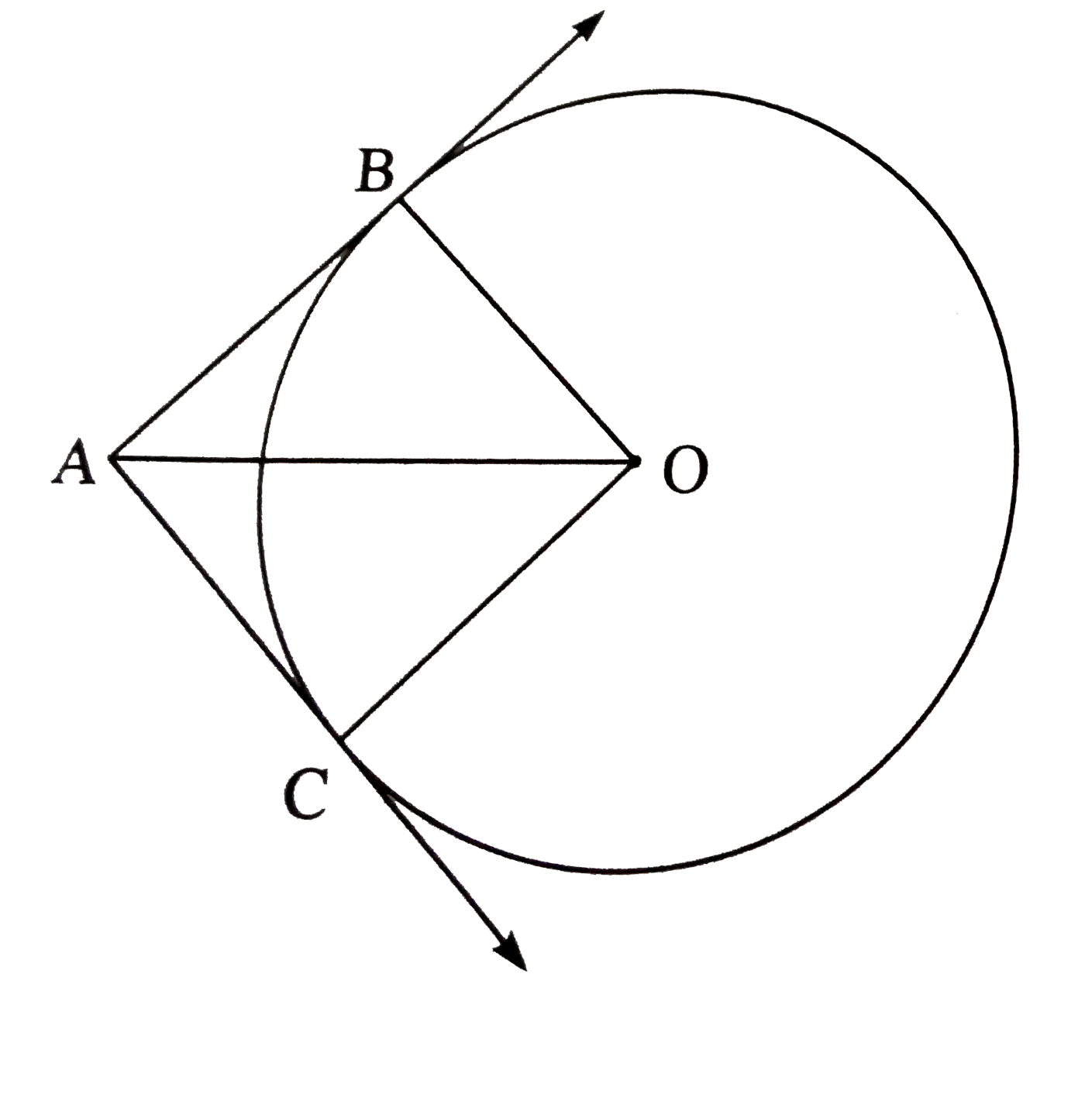 View Solution
View SolutionIn the adjoining figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that , □ ABOC is a square.
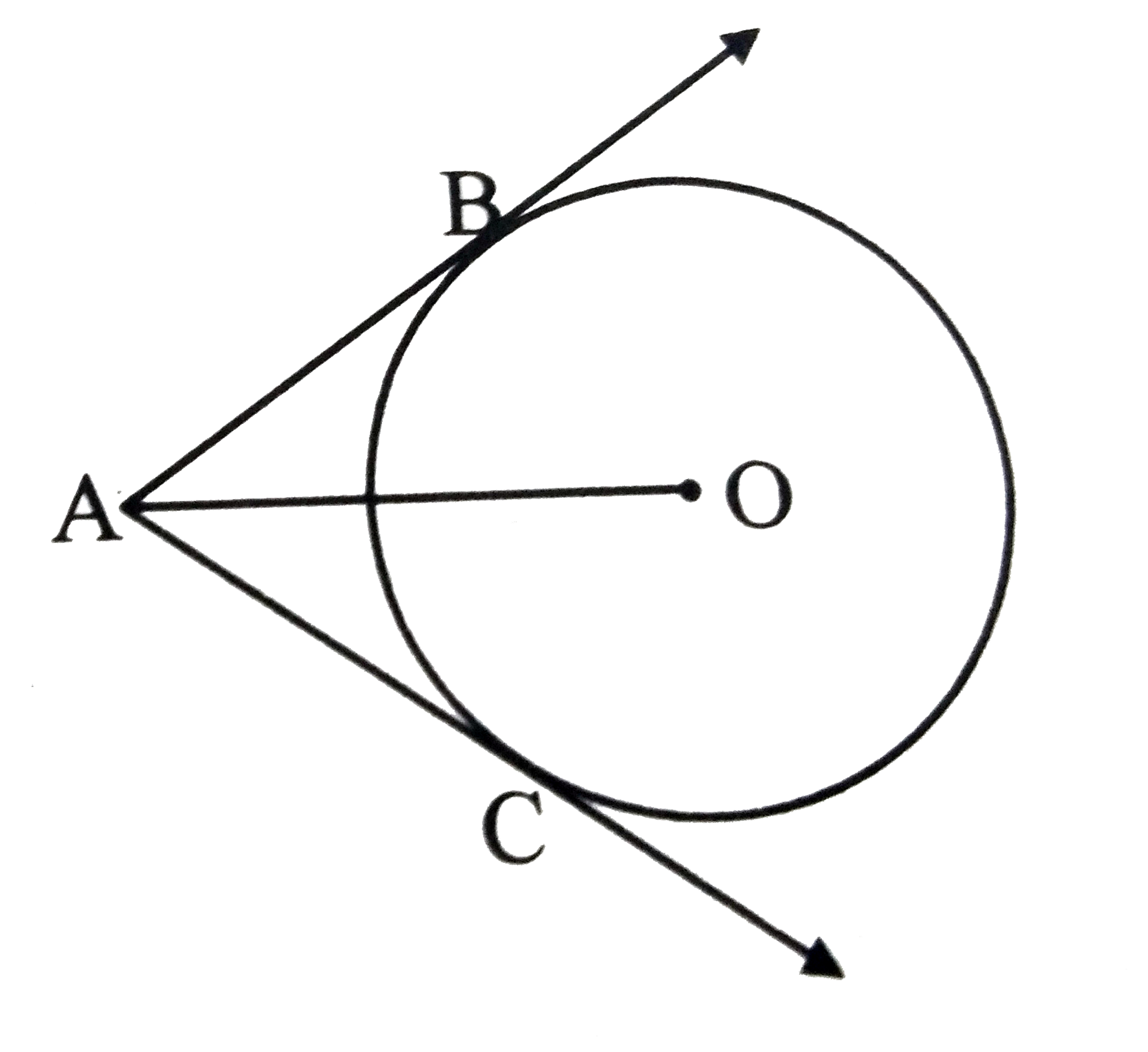 View Solution
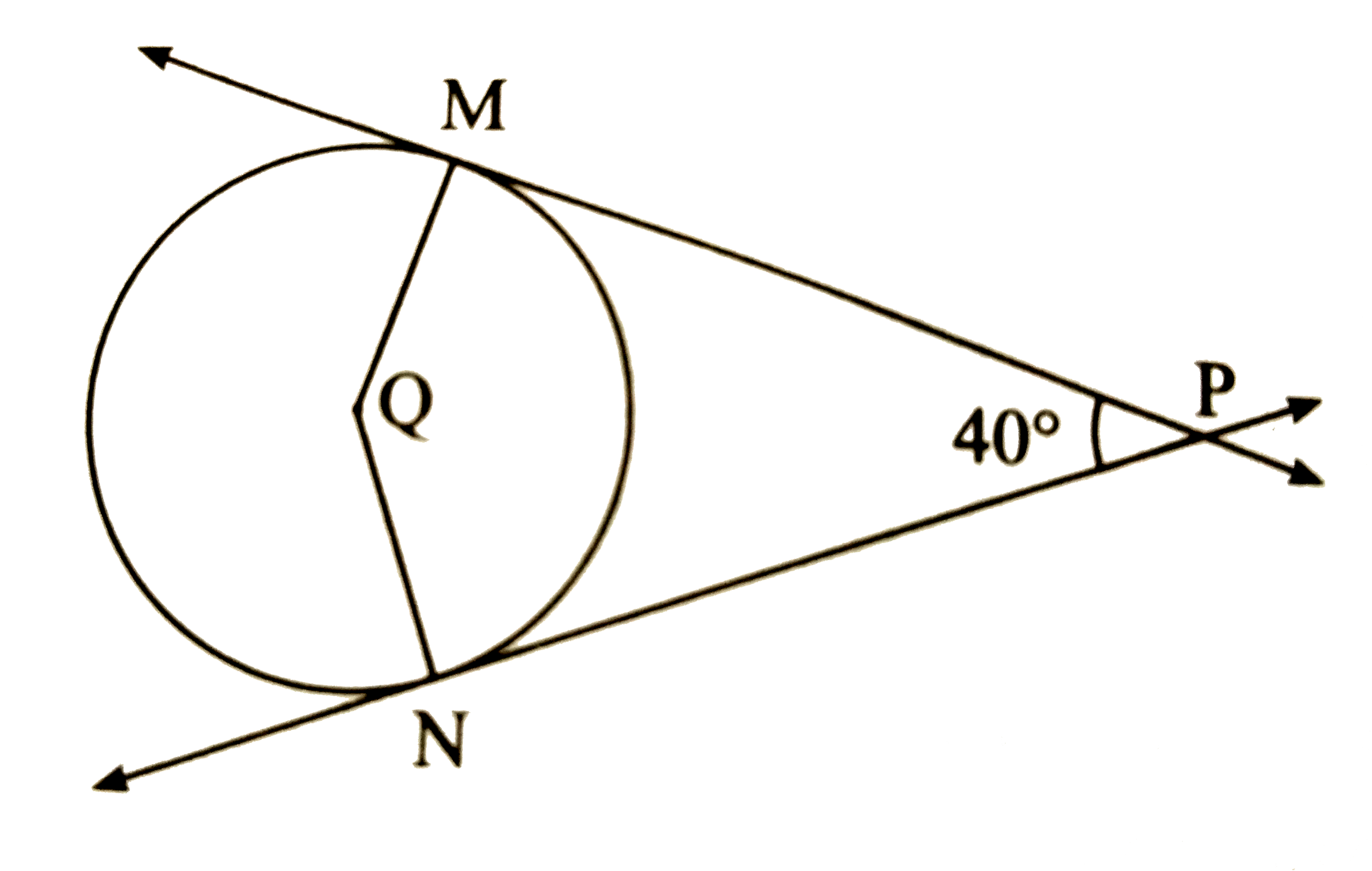
View SolutionIn the given figure, Q is the centre of the circle and PM ,PN are tangent segments to the circle. If ∠MPN=50∘ find ∠MQN.
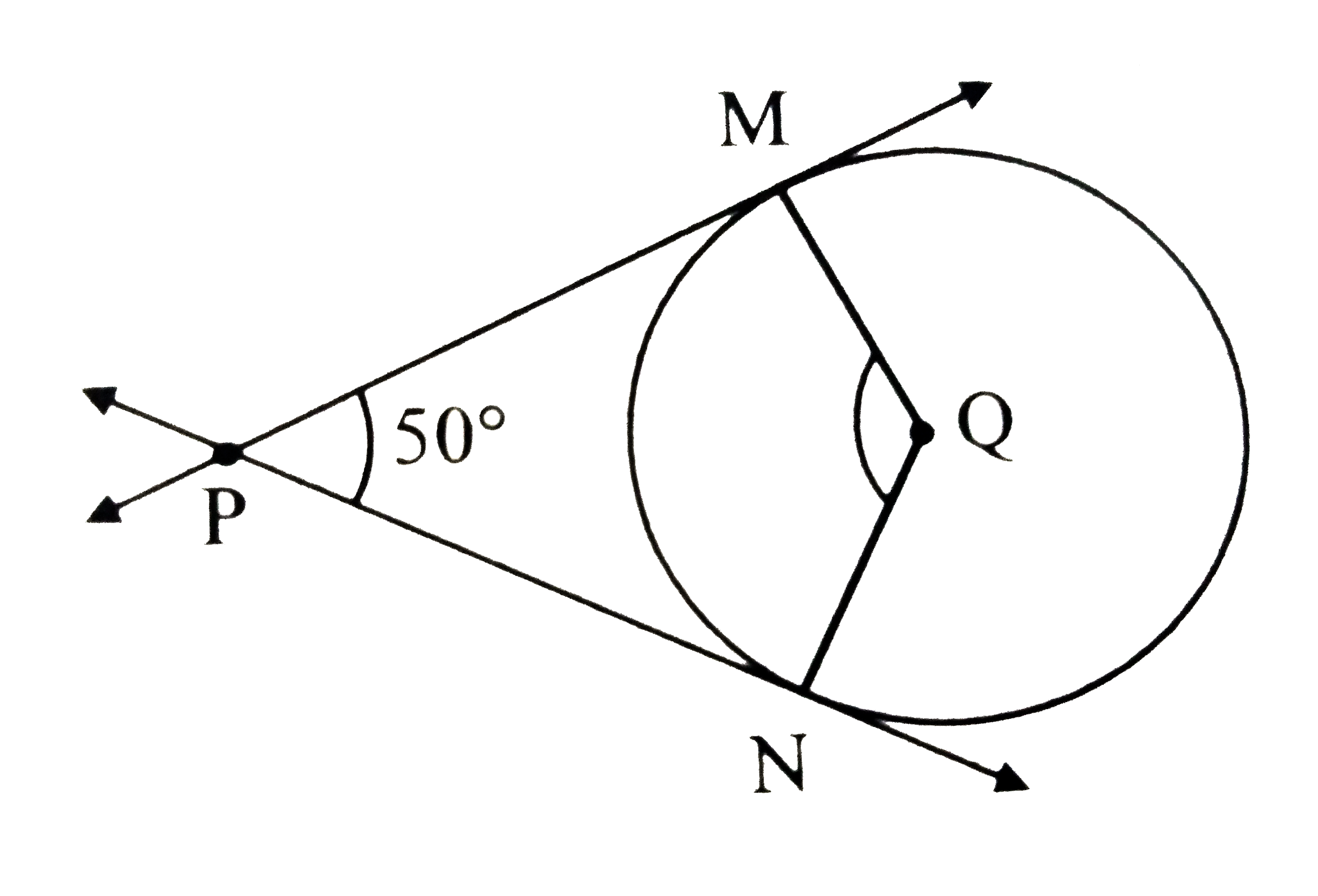 View Solution
View Solution