Question

In the figure , $\Delta QRS$ is an equilateral triangle.
Prove that
(1) arc RS $\cong arcQS\cong$ arc QR
(2) m (arc QRS ) $={240}^{\circ }$.
Proof $:$

Explanation

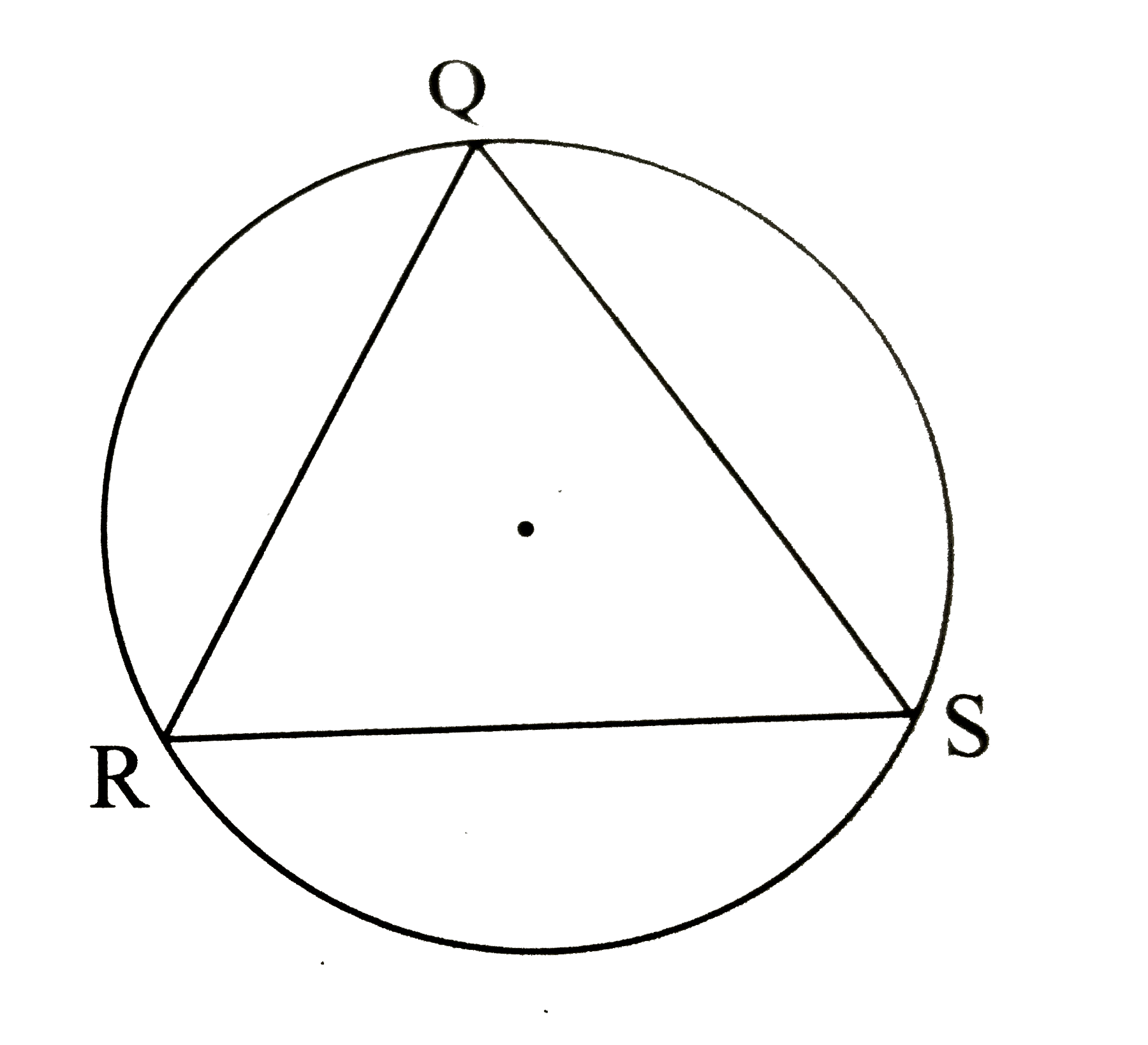
`Delta QRS ` is an equilateral triangle ….(Given )
`:.` seg RS `~= ` seg QS `~=` seg QR …(Sides of equilateral triangle )
Arcs of the same circle are equal, if the related chords are congruent.
`:. ` arc RS `~=` arc QS `~=` arc QR ....(1)
Let m(arc RS ) = m (arc QS ) = m (arc QR ) = x
m ( arc RS ) + m (arc QS ) + m ( arc QR ) ` = 360^(@)` ....( Measure of the circle is `360^(@)` )
`:. x + x + x= 360^(@)` ....[From (1) ]
`:. 3x = 360^(@)`
`:. x = ( 360 )/( 3)`
`:. x = 120^(@)`
`:. ` m ( arc RS ) = m (arc QS ) = m (arc QR )` = 120^(@)`
m(arc QRS ) = m (arc ( QR 0 + m (arc RS ) ....(Arc addition postulate )
`:.` m ( arc QRS ) `= 120 ^(@) + 120^(@)`
`:.` m ( arc QRS ) = `240^(@)`