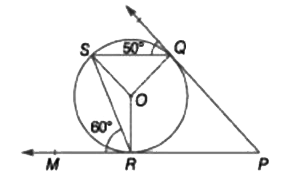
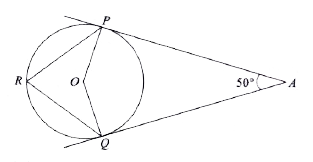
In the figure, O is the centre of a circle,PQL and PRM are the tangents at the points Q and R respectively and Sis a point on the circle such that ∠SQL=50∘and∠SRM=60∘. Then , ∠QSR is equal to
40∘
50∘
60∘
70∘
Since PQL is a tangent and OQ is a radius, so ∠OQL=90∘
∴∠OQS=90∘−50∘=40∘
Now, OQ=OS⇒∠OSQ=∠OQS=40∘
Similarly, ∠ORS=90∘−60∘=30∘
And, OR=OS⇒∠OSR=∠ORS=30∘
∴∠QSR=∠OSQ+∠OSR=40∘+30∘=70∘.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Assertion-and-Reason1videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Test Yourself20videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)15videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself10videos
CONSTRUCTIONS
Similar Questions
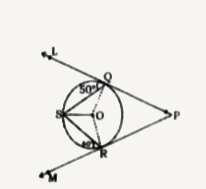
In the given figure, PQL and PRM are tangents to the circle with centre 'O' at the points Q and R, respectively and S is a point on the circle such that ∠SQL=50∘and∠SRM=60∘. Then ∠QSR is equal to
 View Solution
View SolutionPQL and PRM are tangents to a circle with centre O at points Q and R respectively. S is a point on the circle such that ∠SQL=50∘ and ∠SRM=60∘. Find value of ∠QSR.
View Solution
Knowledge Check
- Question 1 - Select One
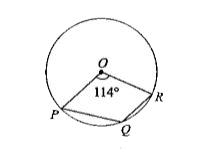
In the figure, O is the centre of the circle . ∠PQR is equal to
 A57∘B63∘C123∘D92∘
A57∘B63∘C123∘D92∘ - Question 2 - Select One
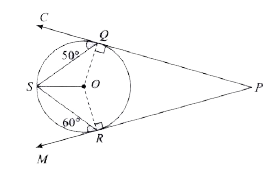
In the figure , PQ and PR are tangent to the circle with centre O. Also, S is a point on the circle such that ∠SQC=50∘and∠SRM=60∘, then ∠QSR=
 A40∘B70∘C80∘D45∘
A40∘B70∘C80∘D45∘ - Question 3 - Select One
In the figure, O is the centre of a circle and AT is a tangent at point A. The measure of ∠BAT is:
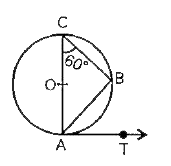 A30∘B60∘C75∘D105∘
A30∘B60∘C75∘D105∘
In the given figure 'O' is the centre of the circle SP and TP are the two tangents at S and T respectively. ∠SPT is 50∘, the value of ∠SQT is:
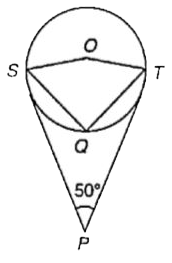 View Solution
View SolutionIn the given figure, O is the centre of the circle, PA and PB are tangents to the circle then find ∠AQB.
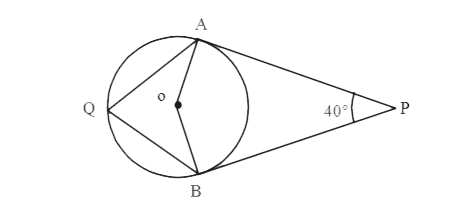 View Solution
View SolutionIn the given figure , O is the centre of the circle . AP and AQ are tangents to the circle .∠PRQ=
 View Solution
View SolutionIn the given figure, O is the centre of the circle . AC and AB are the tangents to the circular at points P and Q , respectively. Also ∠RPC=55∘and∠RQB=60∘ then ∠PRQand∠QAP are, respectively .
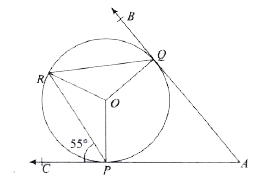 View Solution
View SolutionIn the figure , O is the centre of the circle and BCD is tangent to it at C . Find the value of ∠BAC+∠ACD
 View Solution
View Solution

