In the figure, O is the centre of the circle and B is a point of contact. Seg OE ⊥ seg AD, AB = 12, AC = 8, find (i) AD (ii) DC (iii) DE.
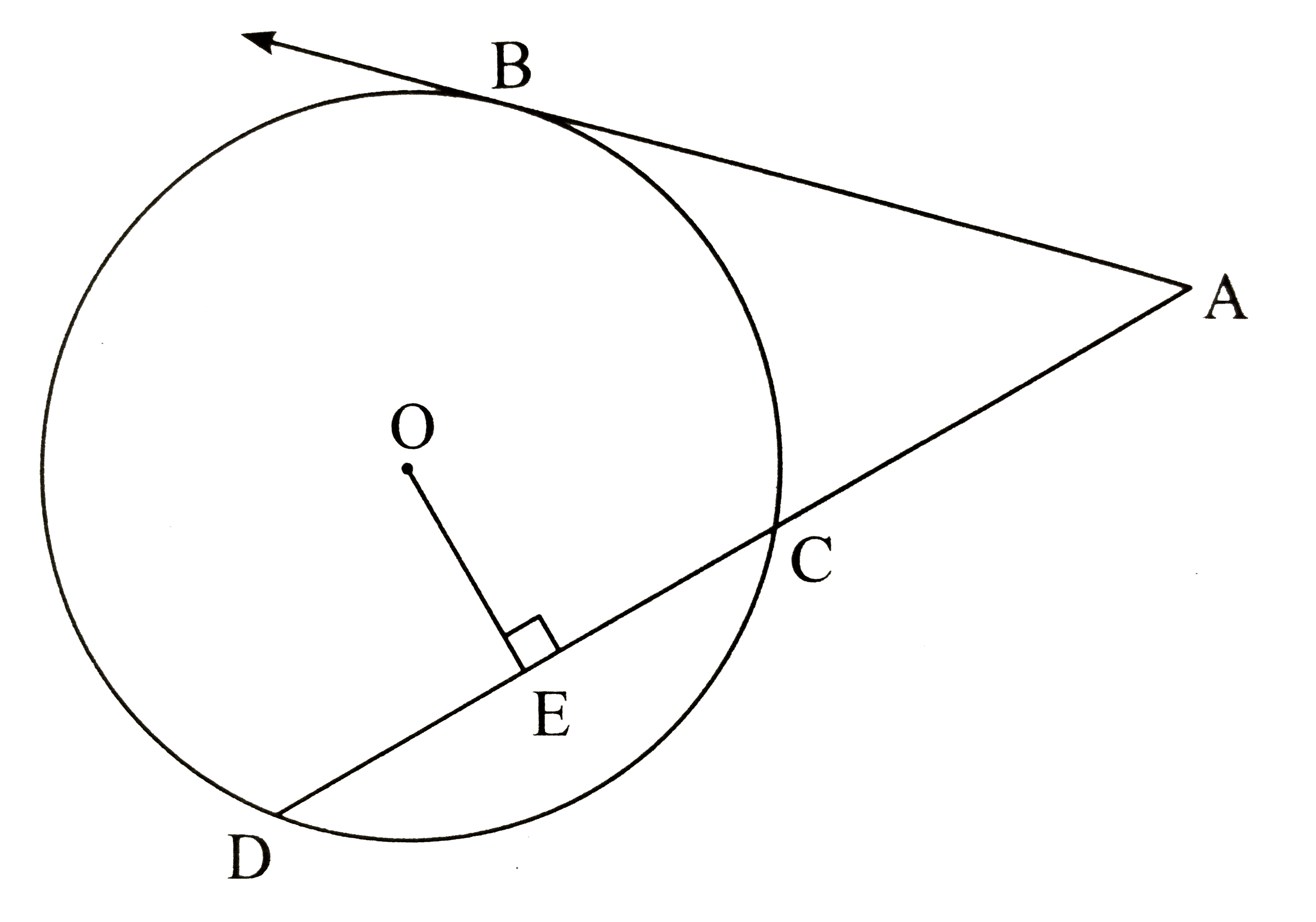
The correct Answer is:(i) ∴AD=1448 (ii) ∴ DC=10 units (iii) ∴ DE=5 units
Step by step video & image solution for In the figure, O is the centre of the circle and B is a point of contact. Seg OE _|_ seg AD, AB = 12, AC = 8, find (i) AD (ii) DC (iii) DE. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Problem Set-325videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Activities for Practice4videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set 3.46videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics4videos
CHALLENGING QUESTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT19videos
CO-ORDINATE GEOMETRY
Similar Questions
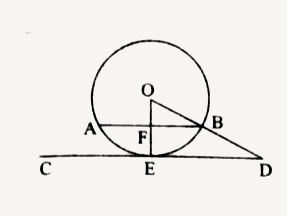
In the figure above, O is the centre of the circle CD is a tangent to the circle at E. OE bisects the chord AB at F. AB = 16 cm and EF = 2 cm. Find the length of DE (in cm).
 View Solution
View Solution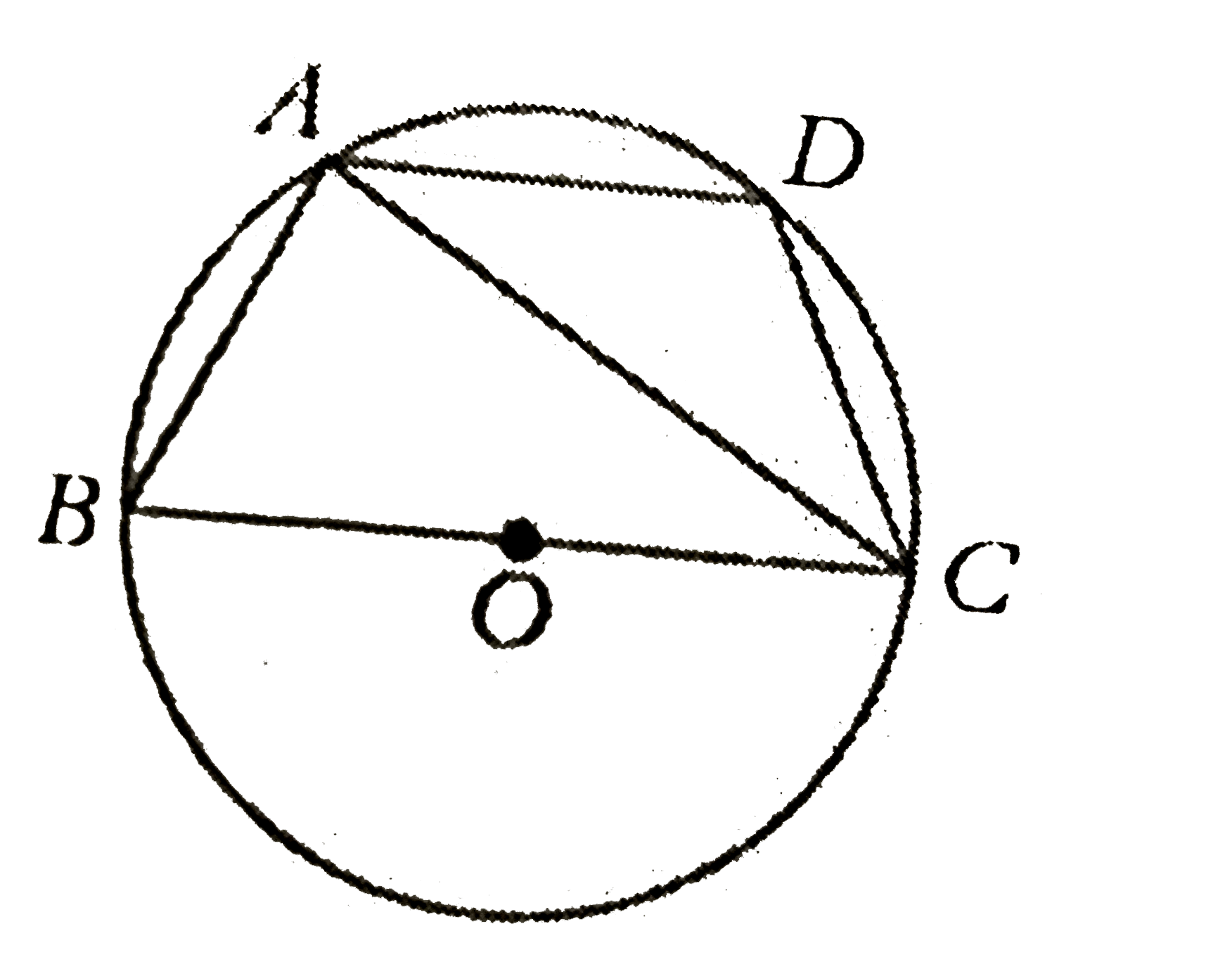
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.View Solution
Knowledge Check
- Question 1 - Select One
In the given figure, O is the centre of the circle. Given that OD = OE = 3 cm and AD = 4 cm. Find the length of the longest chord.
 A6 cmB8 cmC10 cmD9 cm
A6 cmB8 cmC10 cmD9 cm
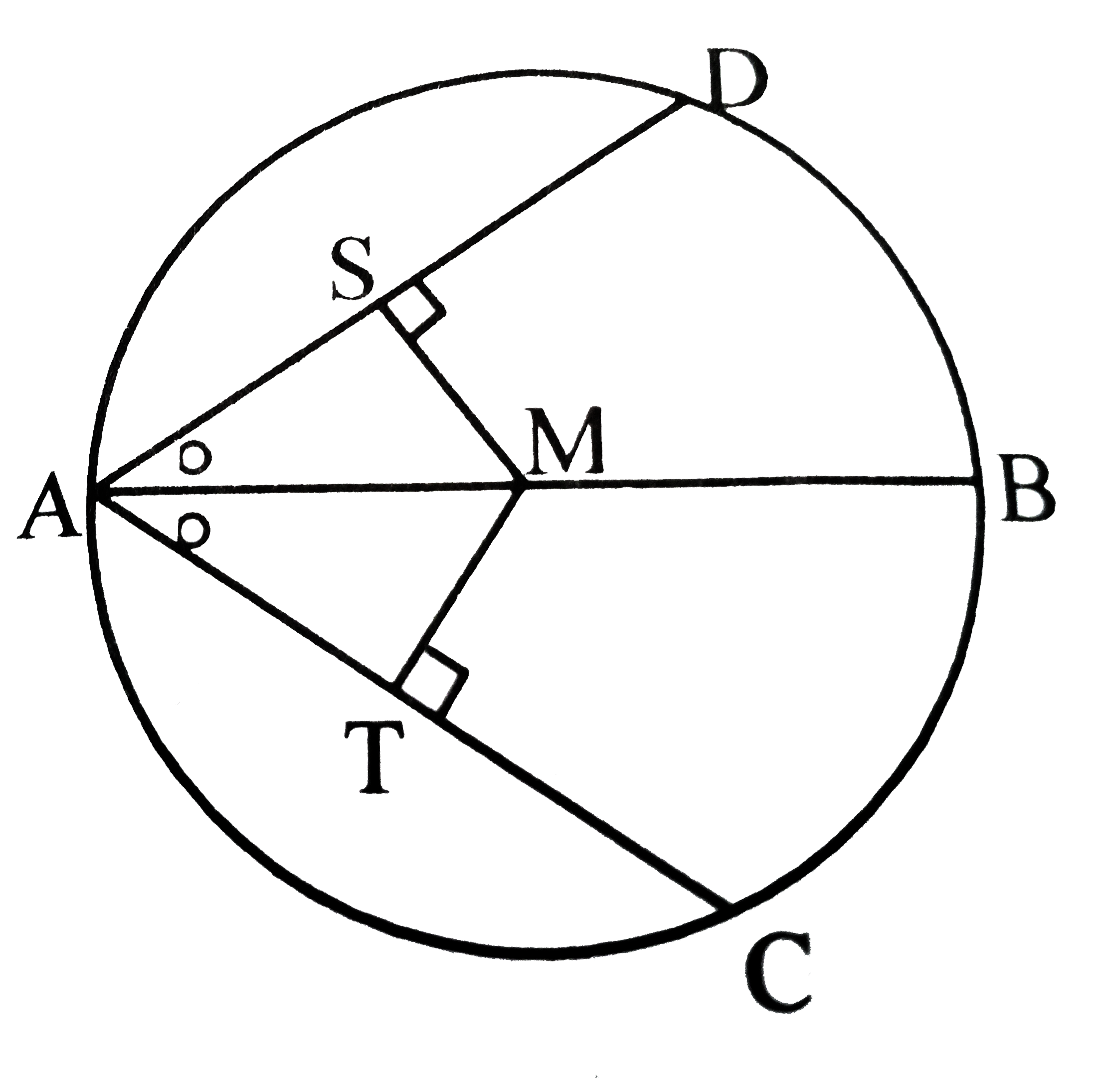
In the adjoining figure, M is the centre of the circle and seg AB is a diameter. Seg MS⊥ chord AD, seg MT ⊥ chord AC, ∠DAB≅∠CAB.
Prove that : chord AD≅ chord AC.
 View Solution
View SolutionIn the figure, O is the centre of the circle . Seg AB is the diameter at the point C on the circle the tangent CD is drawn. Line BD is a tangent to the circle at point B. Show that seg OD ∣∣ chord AC.
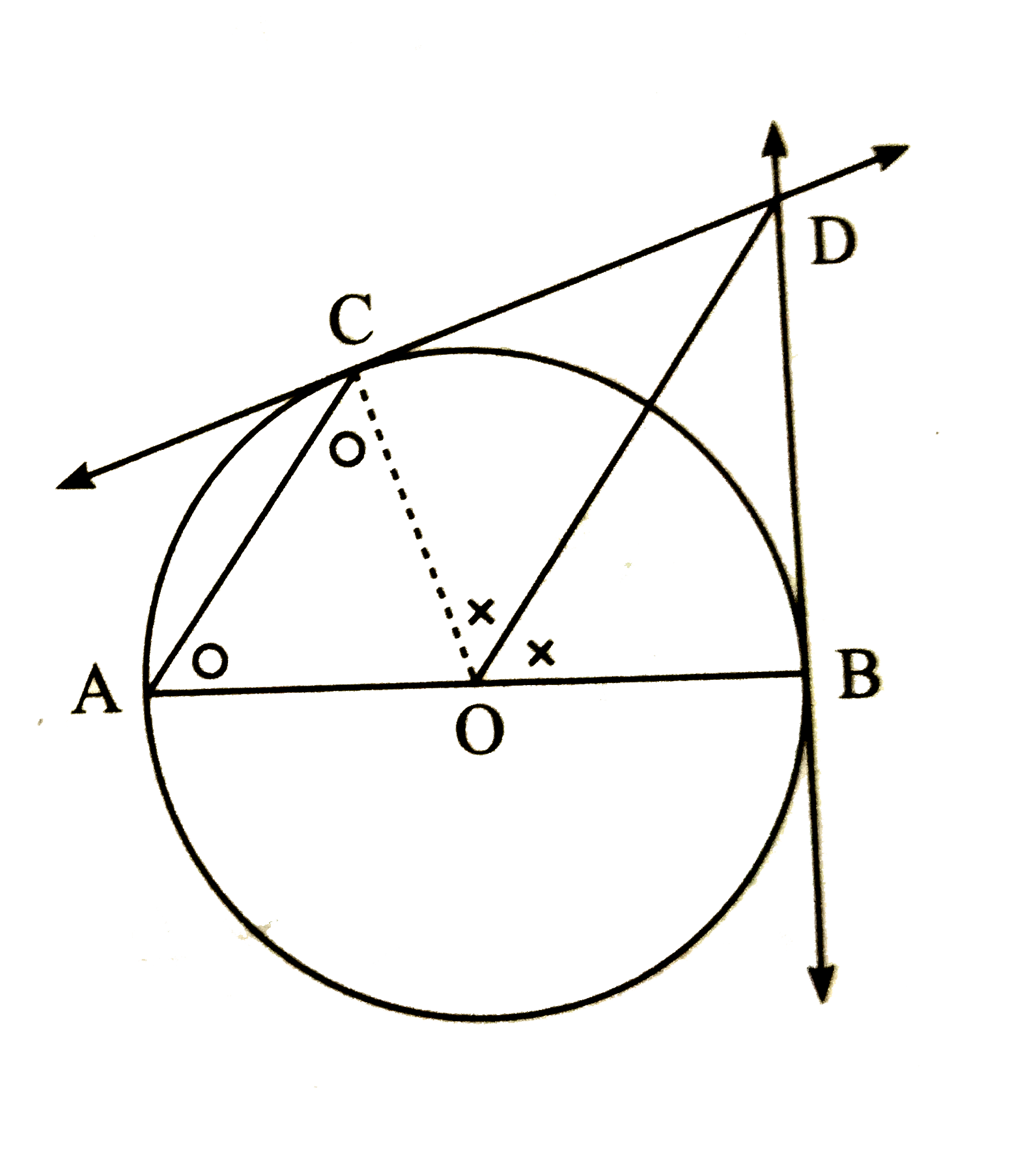 View Solution
View SolutionSolve any two of the following subquestions :
In the figure , O is the centre of the circles and AP is the tangent to the circle at point A . Ray AF is the bisector of ∠BAC
Prove : seg AP≅ seg PE<br>View SolutionIn the figure, O is the centre of the circle of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB)=r. Prove that, □ABOC is a square.
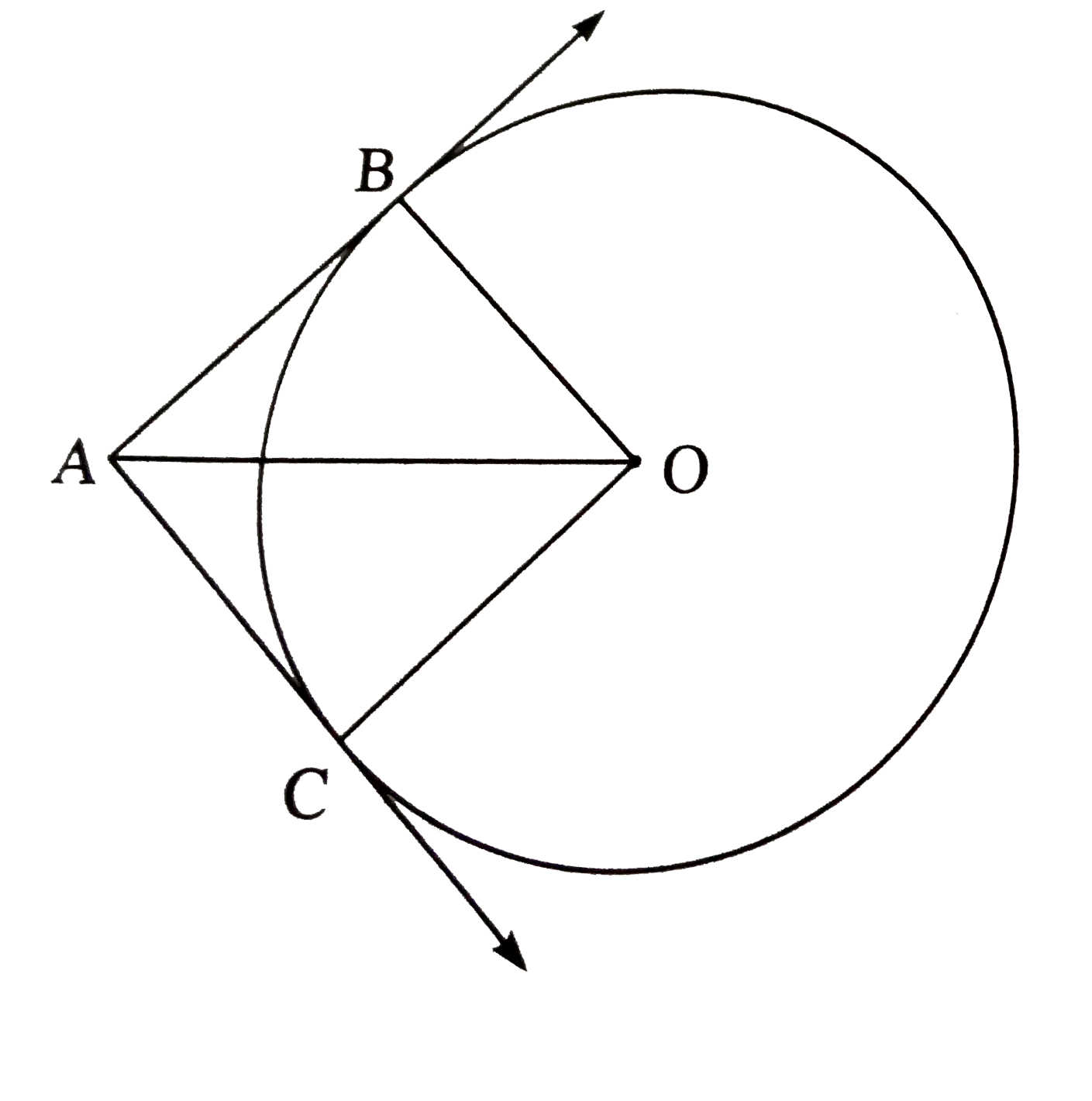 View Solution
View Solution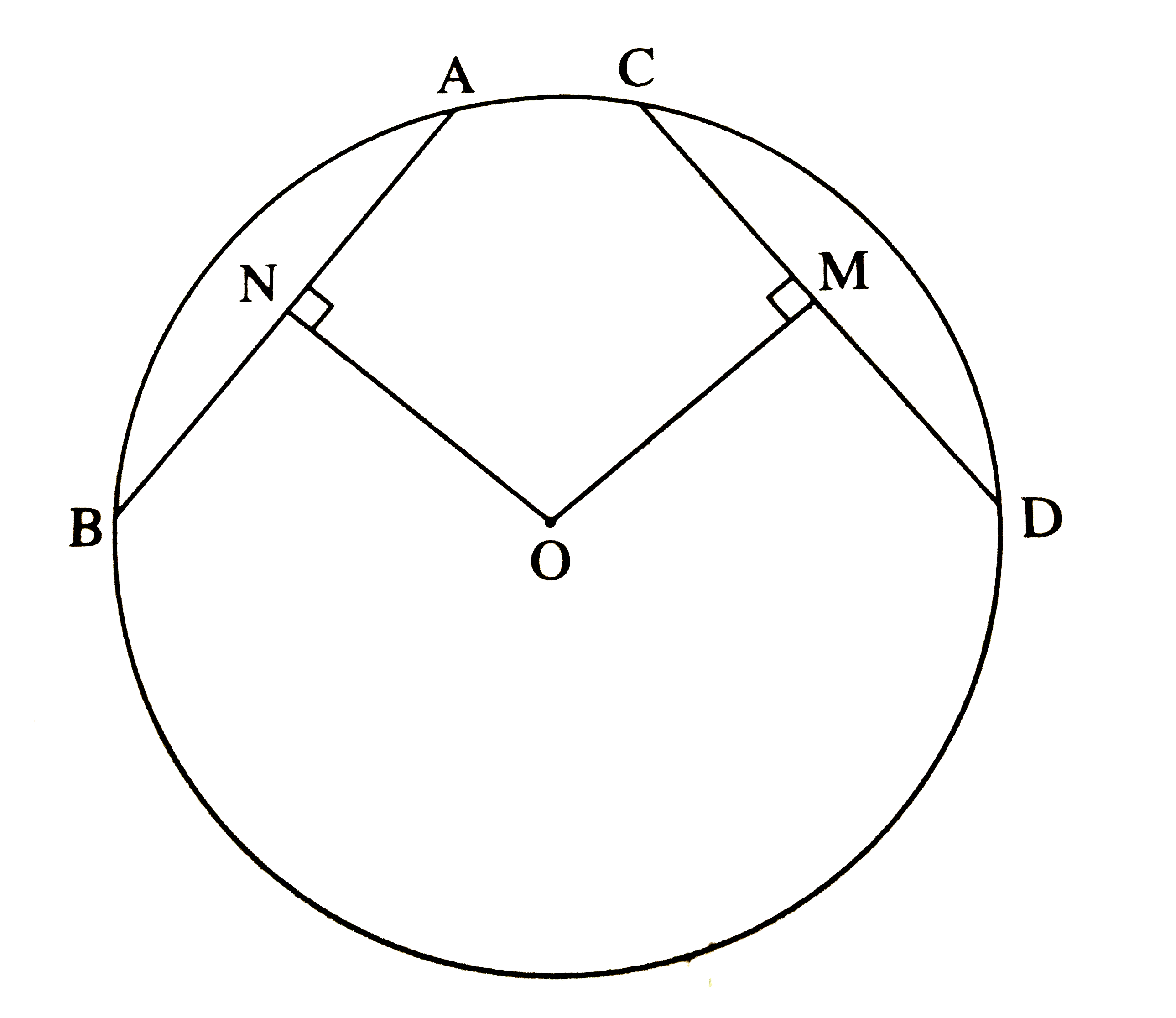
In the figure , O is the center of the circle.chord AB and CD are congruent . If seg ON ⊥ chord AB and seg OM ⊥ chord CD and OM =4cm , then find ON . Justify your answer .View SolutionIf in the figure AB=a,AC=4cm, while D is the circle of the circle and D is a points betbeen O and B such that AD⊥BC.The length (in cm) of OD is
View SolutionIn the figure D is a point on BC such that ∠ABD=∠CAD. If AB=5cm,AD=4cm and AC=3cm. Find (i) BC (ii) DC (iii) A(ΔACD):AIΔBCA).
View Solution

