In the following figure, DE is parallel to BC. Show that :
(i)
(ii) .
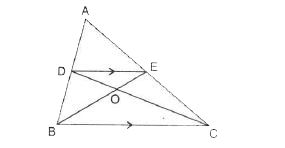
Step by step video & image solution for In the following figure, DE is parallel to BC. Show that : (i) "Area" (DeltaADC)= "Area" (DeltaAEB) (ii) "Area" (DeltaBOD)= "Area" (DeltaCOE). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
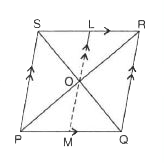
In the given figure, diagonals PR and QS of thr parallelogram PQRS intersect at point O and LM is parallel to PS. Show that :
(i) 2Area(ΔPOS)=Area(//gmPMLS)
(ii) Area(ΔPOS)+Area(ΔQOR)
=12Area(//gmPQRS)
(iii) Area(ΔPOS)+Area(ΔQOR)
=Area(ΔPOQ)+Area(tΔSOR)
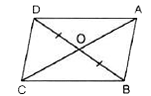
View SolutionIn the given figure, the diagonals AC and BD intersects at point O. If OB=OD and AB//DC, prove that :
(i) Area(ΔDOC)=Area(ΔAOB).
(ii) Area(ΔDCB)=Area(ΔACB).
(iii) ABCD is a parallelogram.
View Solution
Knowledge Check
In the figure, what is the area of ΔABC?
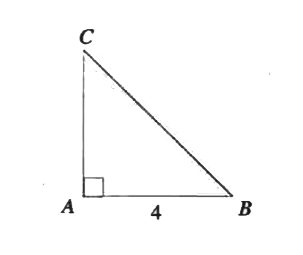 A6B7C8DIt cannot be determined from the information given
A6B7C8DIt cannot be determined from the information givenIn the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2
In the adjoining figure, DE∣∣BC. Prove that area (ΔACD)= area (ΔABE)

View SolutionIn the following figure G, is centroid of the triangles ABC.
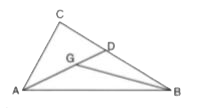
Prove that
Area (Δ AGB )=13× Area (ΔABC)
View SolutionIn the figure, the area of parallelogram ABCD is

View SolutionIn ΔABC, AD divides BC in thr ratio m:n. Show that Area(ΔABD)Area(ΔADC)=mn
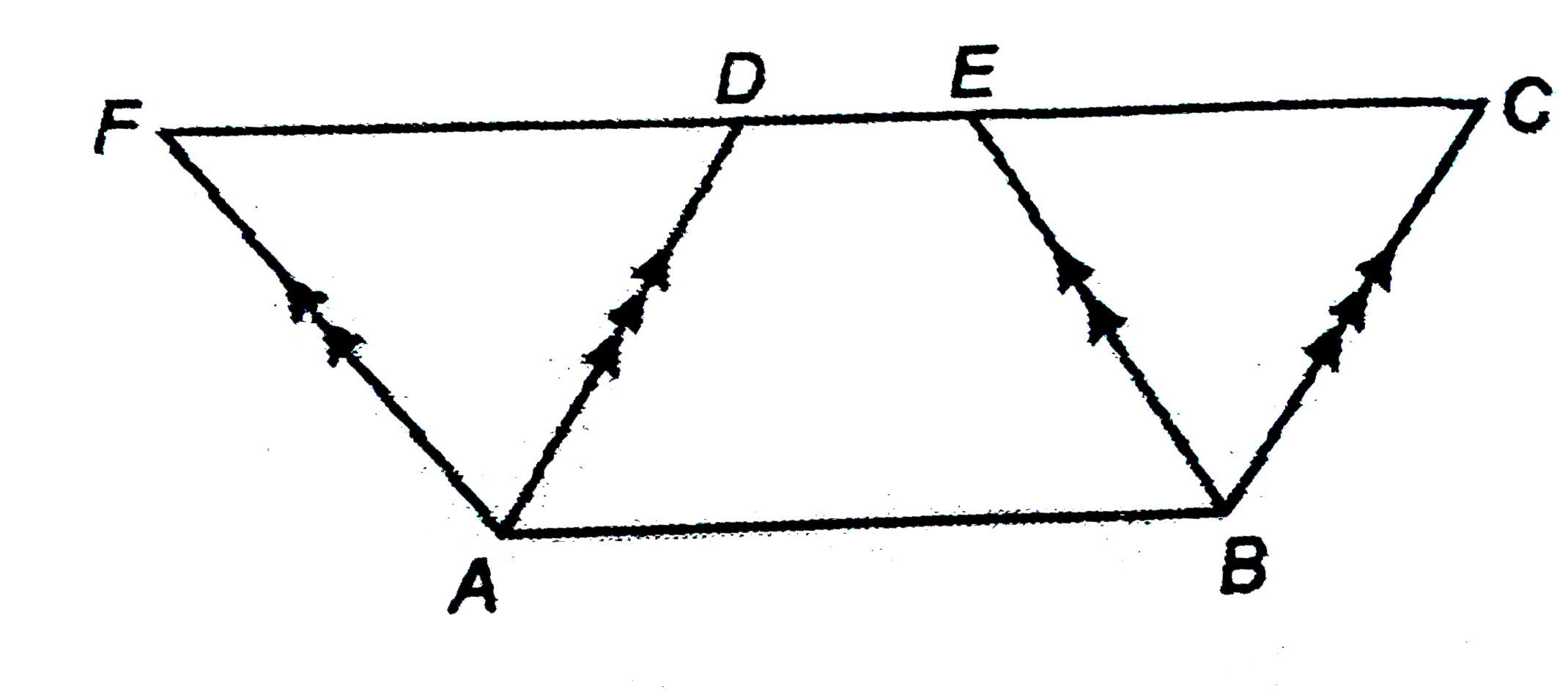
View SolutionThe following figure shows two paralelograms ABCD and ABEF prove that
area of ΔADF=areaofΔBCE
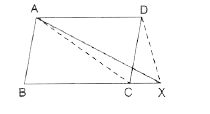
View SolutionIn the given figure, ABCD is a parallelogram BC is produced to point X. prove that :
area(ΔABX)=area( .ACXD)
View Solution
